[백준] 17471번 게리맨더링 - 파이썬/DFS

https://www.acmicpc.net/problem/17471

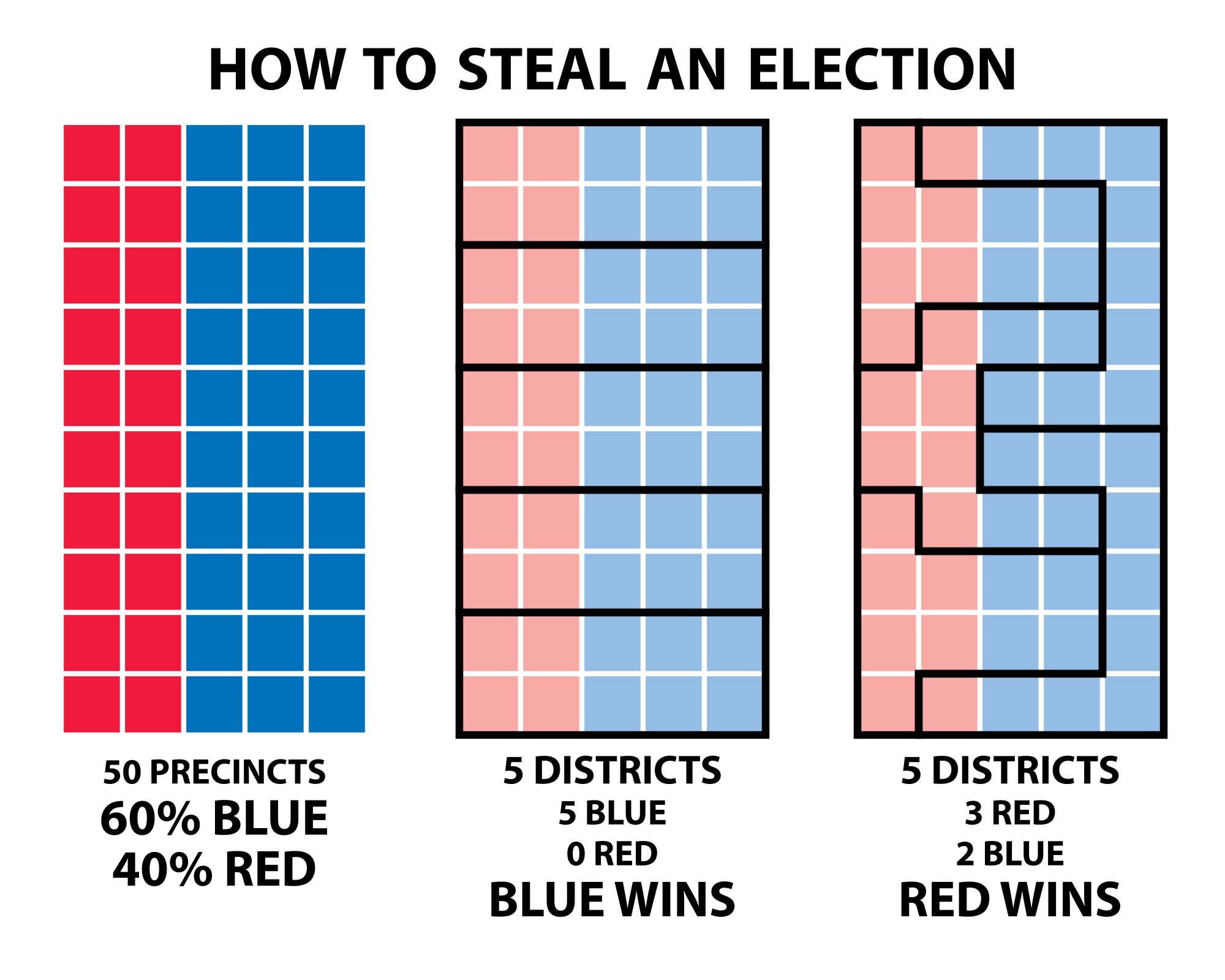
게리맨더링은 아래의 그림처럼 선거구를 유리하게 선정하는 전략을 말한다고 한다.

from itertools import combinations

N = int(input())

nums = list(map(int,input().split())) # 인구수

N_list = [ i for i in range(1,N+1)] # 선거구

case_list = [] # 모든 선거구 케이스를 담는다


# 선거구 케이스를 리스트에 담음
for i in range(1,(N//2)+1):
    first = list(combinations(N_list,i))
    for j in first:
        last = list(set(N_list) - set(j))
        case_list.append( (list(j),last) )


graph = [ [] for _ in range(N+1)] # 인접 그래프

for i in range(1,N+1):

    temt = list(map(int,input().split()))

    adja = temt.pop(0)

    for j in temt:
        if i not in graph[j]:
            graph[j].append(i)
            graph[j].sort()
        if j not in graph[i]:
            graph[i].append(j)
            graph[i].sort()


def dfs(x,visited,elem):
# elem = x의 인접 구역
    visited[x] = True
    for i in graph[x]:
        if not visited[i] and i in elem:
            dfs(i,visited,elem)

ans = 99999999

for case in case_list:

    first = case[0]
    last = case[1]

    visited_first = [ False for _ in range(N+1) ]
    visited_last = [False for _ in range(N + 1)]

    dfs(first[0],visited_first,first)
    dfs(last[0], visited_last, last)

    check = False

    for i in first:
        if not visited_first[i]:
            check = True

    for i in last:
        if not visited_last[i]:
            check = True

    if check:
        continue

    sum_first = 0
    sum_last = 0

    for i in first:
        sum_first += nums[i-1]

    for i in last:
        sum_last += nums[i-1]

    ans_check = abs(sum_first - sum_last)

    ans = min(ans,ans_check)


if ans == 99999999:
    print(-1)
else:
    print(ans)

문제 풀이는 이렇게 접근했다.

1. 선거구를 두개로 나누기

• combinations을 활용하여 N의 갯수의 절반만큼 반복을 시행한다.
• 조합이 첫번째 선거구, 전체에서 첫번째를 뺀 구역이 두번째 선거구이다.

2. 나뉜 선거구에 DFS를 적용하여 연결되어있는지 확인하기

• 선거구 첫번째 점에서 DFS를 한다.
• 만약 선거구에서 방문하지 않은 구역이 있으면 제외한다.

3. 2번 조건을 통과했다면 두 선거구의 인구 차이를 구하기

4. 인구 차이의 최소값 구하기