[BOJ][python] 21758_꿀따기

문제 이름 : 21758_꿀따기

---

풀이 :

• Key point :
• 그리디 탐색은 미래는 생각하지 않고 현재에 가장 최우선의 선택을 한다가 뽀인트이다. 그리고 선택은 되돌릴 수 없다 !
• Logic :

N 개의 장소가 있고 두마리의 벌과 한개의 꿀통이 있다.

1. 벌들은 꿀통 쪽을 향해서만 이동이 가능하다.
2. 벌들이 처음 있었던 장소에서는 꿀을 딸 수가 없다.

가장 많은 꿀을 딸 수 있는 경우를 생각해보면 꿀통은 아예 양 끝쪽에 있거나 중간에 있는 경우다.

아래 그림과 같이 세가지가 나온다.

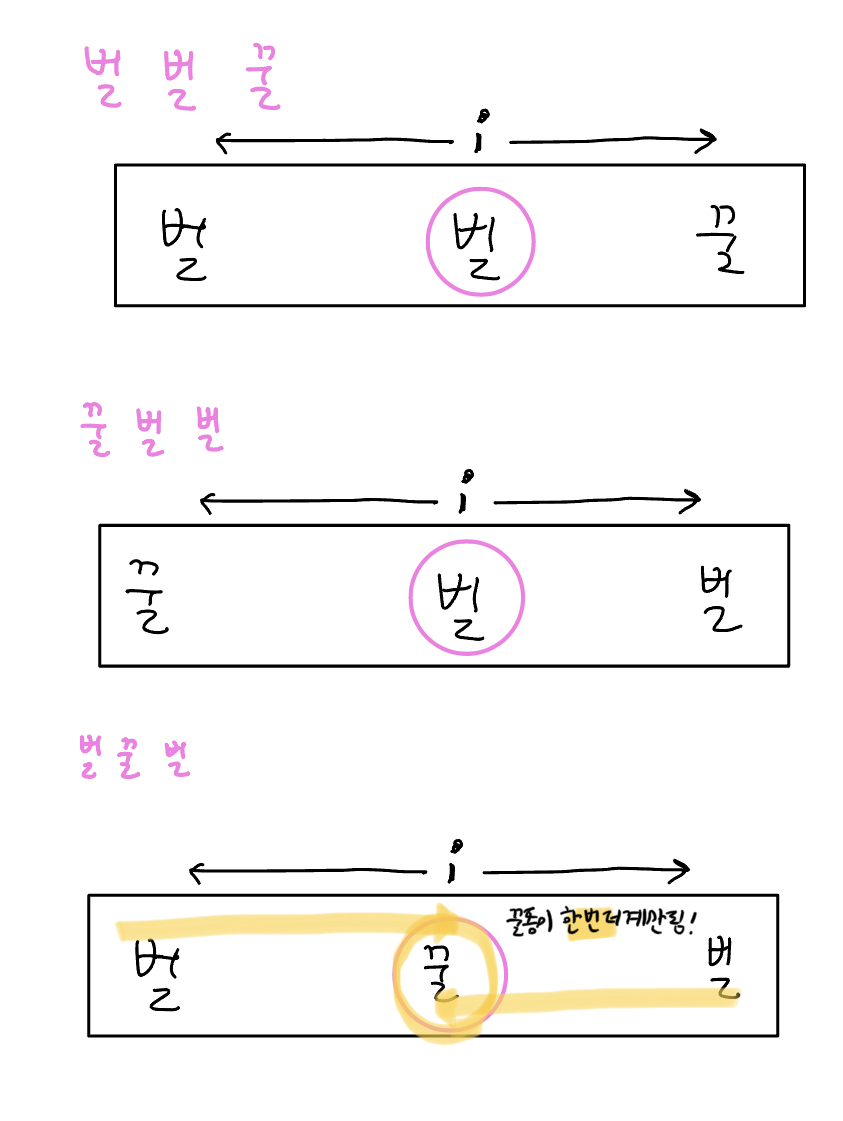
벌 벌 꿀 인 경우

꿀 통이 오른쪽에 있을 경우 벌들 중 한 마리는 무조건 꿀 통의 반대편 끝쪽( 왼쪽 끝 값)에 있는 편이 유리하다. 나머지 한 벌은 양 끝쪽 중간 어딘가에 위치할 것이다,, 이 벌이 어디에 있는 지에 따라 최대 누적 합이 달라지게 된다. 이 벌의 위치를 움직여봐야한다. 그래서 이 벌의 위치를 i 라고 둔다.

꿀 벌 벌 인 경우

벌 벌 꿀을 활용해서 생각하면 쉽게 이해 가능하다.

벌 꿀 벌 인 경우

가장 큰 누적 합을 n-2 번 굳이 돌려볼 필요가 없이 바로 한번에 알 수 있다.

꿀통에 중간에 위치한 경우 : 0부터 N-1 까지의 합 + 꿀통 - ( 두 벌의 시작 자리의 합)

꿀통이 한번 더 더해지는 셈이니 가장 큰 값을 선택하면 된다.

# 다른 블로그 참고
import sys

input = sys.stdin.readline

n = int(input()) 
ndata = list(map(int,input().split())) 
prefix_sum =[0 for _ in range(n)]   # 누적 합

prefix_sum[0]= ndata[0]
for i in range(1,n):        # 누적합 구하기 
    prefix_sum[i]+=prefix_sum[i-1]+ ndata[i]

honey =0

#  벌 벌 꿀
for i in range(1,n-1):
    temp = 2*prefix_sum[n-1] - prefix_sum[i] -(ndata[0]+ndata[i])
    honey = max(honey, temp)

#  꿀 벌 벌
for i in range(1,n-1):
    temp = prefix_sum[n-1]-(ndata[n-1]+ndata[i]) +prefix_sum[i-1]
    honey = max(honey, temp)

#  벌 꿀 벌
max_middle = max(ndata[1:n-1])
temp = prefix_sum[n-1]+ max_middle - (ndata[0]+ndata[n-1])
honey = max(honey, temp)

print(honey)

---

전체적으로 느낀점 :

여러 개의 경우로 나누어서 생각해야하는 문제를 어려워하는 것 같다.

꿀다기의 문제도 조금만 더 생각해보면 답이 나올 것 같았지만 결국 다른 블로그를 참고해서 문제를 풀었다.

그래도 예전에는 조금만 복잡하면 문제 접근 방식 자체를 못했는데 , 이제는 예전보다는 훨씬 좋아진 것 같다. !!