💡 Union Find 가 뭐야 ?

쉬어가기

프로그램의 성능 분석

입력 크기에 따라 1. 실행 속도 2.메모리 사용량이 어떻게 변하는지 예측

원하는 성능에 미치지 못하는 경우 원인 파악하여 수정

프로그램의 성능 표현 방법

~f(N) : 입력 데이터의 크기가 N 일 때, 프로그램의 성능이 대략적으로 f(N)에 비례

매우 정확한 성능 개선보다는 대략적으로 서로 다른 알고리즘 간의 차이를 큰 틀에서 빠르게 파악하는 것이 중요

---

들어가기

Union Find 알고리즘이란?

0 ~( N-1 ) 까지 정점으로 표현된 노드들(혹은 연결 상태가 동적인 노드들)을 서로 연결(Union)해가며 연결 여부(Find)를 확인해보는 알고리즘
Disjoint set 알고리즘이라고도 불리며 아래의 2가지 명령 을 수행한다.

• Union(a,b) : a 와 b 를 간선으로 연결
• Connected(a,b) : a 와 b 연결하는 경로 존재하는지 True/False 로 응답

Union Find 활용 예시

• 두 점 간 연결되었는지(connectivity) 확인하며 간선 계속 추가해보는 동적 상황(원하는 상태가 되도록 간선을 조금씩 더 해보는 상황)
• 연결 상태를 조금씩 받아오는 동시에 연결 상태 확인하는 상황
• 그래프 전체가 미리 주어지고 그 형태가 고정적인 상황에서는 알맞지 않다. (단순히 최단 경로나 연결 여부를 알아야되는 경우는 DFS, BFS 알고리즘이 적절)

Union Find 알고리즘을 설계해보자.

방법 1 : adjacency list

Union(a,b)와 Connected(a,b)를 수행하기 위해서는 그래프 연결 상태 저장 필요하다.
adjacency list 방식은 adj[v] 에 v 에 인접한 정점 목록을 저장하는 것이다.

1. adj[4]=[2,5] : 4번 정점에 정점2,5가 연결되어 있음
2. Union(1,2) → adj[1]=0,2 , adj[2]=4,1
   1. 상수시간 소요됨
3. Connected(5,2) → 5→3 ,5→4→2
   1. 운이 나쁘면 모든 간선을 다 뒤져야 된다.

시간복잡도

Union(a,b) ~1

Connected(a,b) ~e(총 간선의수)

문제점
connected(a,b)의 경우 운이 나쁘면 모든 간선을 다 뒤져야 함

방법 2 : Quick Find

“Find(Connected) 할 때 걸리는 시간을 좀 줄여보자” 라는 의미에서 고안된 방법이다.
각 객체가 어느 Connected component에 속하는지 크기 N의 배열에 기록 및 업데이트를 하는 것이다.
Connected component 란 서로 연결된 정점들의 maximal한 집합이다.

1. 총 connected component 의 갯수 : 3
2. 서로 다른 connected component에 서로 다른 id 부여.
3. id는 connected component 에 속한 객체 중 가장 작은 번호 부여
4. union(5,2) 를 하게되면 ids에 있는 모든 index의 값을 돌면서 2인 부분을 1로 바꾼다.
5. union(0,3) 을 하게되면 0이 더 작으므로 2로 되어있던 값을 모두 0으로 바꾼다.

시간 복잡도

Union(a,b) : ~N

Connected(a,b) : ~1

문제점

union(a,b) 시, 바꿀 값이 1개든 N개 이든, N만큼 다 확인해야한다.

내재된 값이 작은 수일 경우, 그 수로 바꾸기로 하였는데, connected component 요소의 갯수를 고려하지 않아 훨씬 더 많이 바꾸게 되는 경우 발생한다.

방법 3: Quick Union

“Union 의 효율을 좀 더 높일 순 없을까?”
Connected Component를 tree로 해석하여 Union 할 때 모든 객체가 아닌 root만 옮겨 붙임으로서 속도를 향상시킬 수 있다.

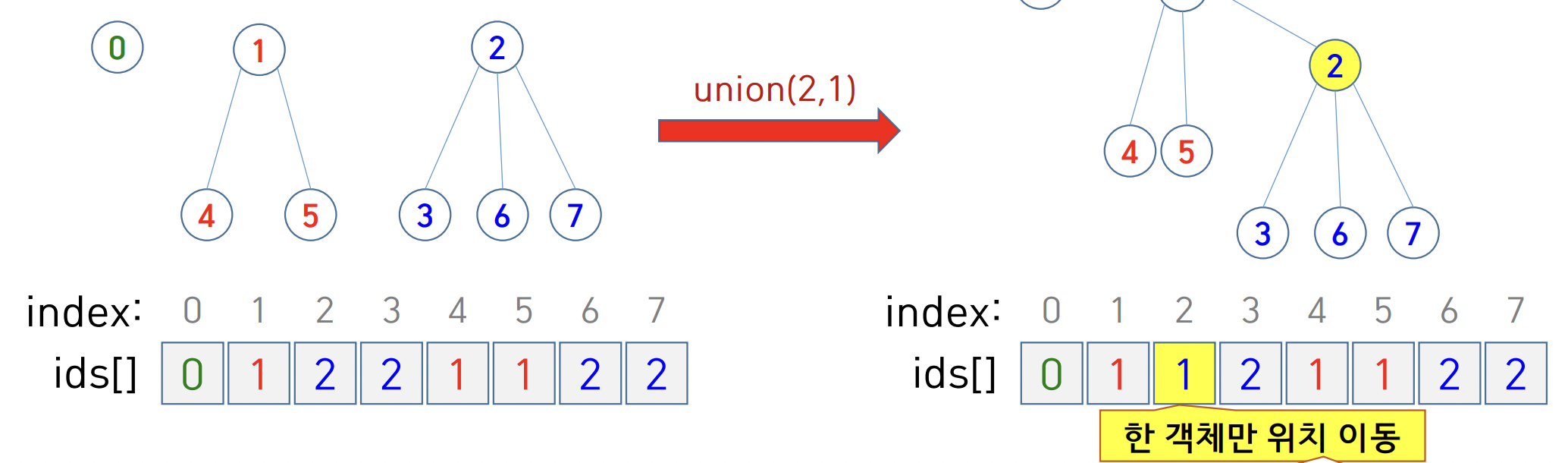
1. ids[i] : 객체 i의 parent
2. 만약 객체 i 가 root라면 ids[i]=i
3. connected(p,q) == True if root(p)==root(q)
4. union(p,q) : root(p) 를 root(q) 아래로 옮겨 붙이기

위에서 알 수 있듯이, QF의 경우에는 모든 정점의 값을 다 바꿔줘야 했지만, QU 는 root의 값만 변경시킨다.

시간복잡도

Union(a,b) : ~d

Connected(a,b) : ~d

in worst case, ~N, ~N

문제점

트리의 깊이를 d 라고 할때,

union(p,q) , connected(p,q) 에서 root를 무조건 찾아야하므로 평균적으로는 ~d, ~d 만큼 걸린다.

하지만, 운이 안 좋을시에는 ~N, ~N 만큼 걸리게된다.

방법 4: WQ

“Tree의 depth를 안 깊어지게 만들 순 없을까?”
Weighted QU를 사용하면 트리 깊이를 제한 할 수 있다
Weighted QU 란 QU 방법이지만, union(p,q)시, 작은 트리의 root를 큰 트리의 root 아래로 연결하는 조건을 추가한 것이다.

depth를 최소로 유지시키기 위해 균형잡힌 tree를 사용한다 . 따라서 WQU를 사용하면 최대 logN 시간에 가능하다.

시간복잡도

Union(a,b) : ~logN

Connected(a,b) : ~logN

최종 코드 구현 (WQU)

```python
#최종 WQU 구현

N=10

ids=[]
size=[]
for idx in range(N):
	ids.append(idx)
	size.append(1)

def root(i):
	while i != ids[i]: i=ids[i]
	return i

def connected(p,q):
	return root(p)==root(q)

def union(p,q):
	id1,id2 = root(p), root(q)
	if id1 == id2 : return
	if size[id1] <= size[id2]:
			ids[id1]=id2
			size[id2]+=size[id1]
	else:
			ids[id2]=id1
			size[id1]+=size[id2]

			
	
```

본 게시글은 수업 시간에 배운 내용을 토대로 작성되었습니다. (출처: 경북대학교 이시형 교수님 PPT 자료 )