[BOJ][python]1188_음식평론가

문제

예제 입력 :

# 예제 입력 : 소시지의 수 N과 평론가의 수 M
	2 6  
# 예제 출력 
	4

1188번: 음식 평론가

풀이 :

• Logic :

  • 소세지 3개를 5명에게 나누어 준다고 상상해보자
    

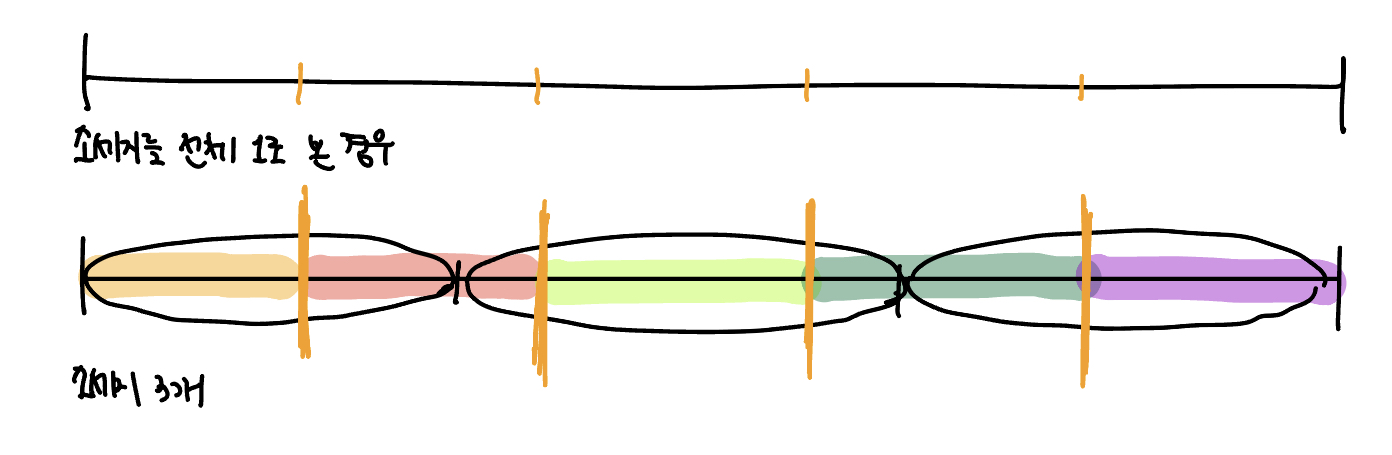
      1개였으면 공평하게 1/5 씩 가져가면 된다. 그런데 3개가 있으니 3/5 씩 가져가면 된다.

    3/5가 3이 되기 위해서는 5토막을 내면 된다. 5토막을 내기위해서는 칼질 4(5-1)번만 하면 된다.

    그림을 보게되면 주황색 선이 최종적으로 시행한 칼질이다.

    여기서 포인트는 3개를 붙여 한개로 보고 생각한 것이다. 3 은 왜 무시해도 되냐고 묻는 다면 3개를 전체로 보고 5토막을 가져가면 되는데 전체가 이미 3토막으로 잘라져있으니까 몇 명은 조각조각이 모인 3/5 를 가져가게되는 셈이다. 따라서 모두 같은 양을 받게된다.

    그럼 무조건 M-1 이 답이냐고 묻는 다면 ? 아니다. 최악의 경우에 M -1 인 셈이다.

  • 소세지 3개를 6명에게 나누어 준다고 상상해보자

    

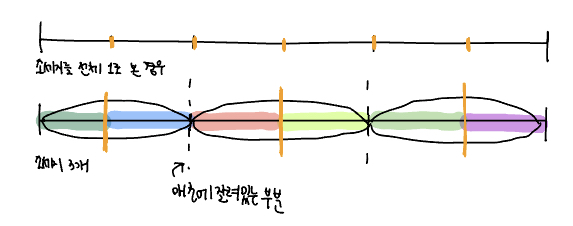
    위와 같은 원리를 적용시켜보면 소세지 3개가 있으니 다들 3/6 즉 1/2 씩 가져가면 된다.

    1/2이 3이 되기위해서는 6토막을 내면 된다. 따라서 ****칼질 5(6-1) 번이 필요하다.

    이게 최선일까? 아니다. 왜냐하면 칼질이 소세지와 소세지를 가상으로 연결시켜 놓은 경계 부분과 겹치기 때문이다. 그림에서 주황색 선을 보면 총 3번의 칼질을 하게된다. 애초에 소세지와 소세지 사이의 경계부분이 칼질 해야하는 부분과 겹친다. 따라서 총 3(6-3)번의 칼질만 필요하다.

    그럼 우리는 어떻게 문제를 풀면될까?

    두 케이스의 차이점을 곰곰히 생각해보면 첫번째 케이스 3과 5사이에는 겹치는 부분이 존재하지 않았지만 두번째 케이스 3과 6 사이에는 겹치는 부분이 발생한다. 3과 6의 최대공약수는 3이다. 반면에 5와 3의 최대공약수는 1이다. 우리느 여기서 M - gcd(M,N)이 라는 식을 유도해 볼 수 있다.

코드 :

import sys
input = sys.stdin.readline

N, M = map(int,input().split()) # N : 소세지 수, M : 음식평론가 수

def GCD(a,b):   # a 와 b 의 최대 공약수를 찾아주는 함수 (a 와 b 대소 관계 필요 없음 )
    r = 1       # 임의의 수 넣어두기
    while(r):
        r = a % b
        a = b
        b = r
    return a

print(M-GCD(N,M))