1. 베이즈 정리?
넷플릭스에서 쓰이는 알고리즘이라고 한다. 그만큼 중요한 알고리즘이기 때문에 익힐 필요가 있다.
베이즈 정리의 특징
베이증 정리의 특징은 최신 정보로, 확률이 바로 업데이트 된다는 점이다. 자율주행 자동차를 예시로 들어보자. 갑작스럽게 발생하는 데이터를 바로바로 확률로 처리해주어 발생하는 문제에 대해 빠르게 대응할 수 있다.

B가 일어나면 A에 대한 확률이 바뀐다는 의미.
조건부 확률(Conditional Probability)
P(A | B):
B가 일어난 전제(조건) 아래 A가 일어날 확률
종속 사건이라고 이해를 하면 편하다. 예시를 들어보자.
💡 **[예시]**예시#1) 100개 중 수 하나
P(A) = 1/100
예시#2) 일의 자리가 5
5, 15 ··· 95 : P(A|B)= 1/10
예시#3) 짝수
P(A|B) = 1/2
2. Likelihood
베이즈 정리를 위한 필수적인 내용인 Likelihood는 가능성, 우도를 뜻한다.
어떤 클래스가 어떤 현상을 통해 벌어지는 가능성을 의미한다. 예시를 들어보자. “구매를 할 고객은 80%로 점원에게 말을 건다”라는 가능성도 Likelihood라고 표현할 수 있는 것이다.
클래스를 B(Buy) 라고 한다면 B가 아닌 클래스는 ㄱB라고 표현한다
현상는 T(Talk) 라고 한다면 T가 아닌 클래스는 ㄱT라고 표현한다
💡 **ㄱB:** B가 아닌 클래스. not 을 의미 **ㄱT:** T가 아닌 현상구매”클래스”가 말을 거는 “현상” 했을 떄의 경우의 수
그렇다면 이 경우의 수를 표현한다면 몇 가지가 나올 수 있을까? 총 네가지로 표현할 수 있다.
💡 P(T | B): 구매클래스 중 말을 건 현상 P(ㄱT | B): 구매 클래스 중 말을 걸지 않은 현상 P(T |ㄱB): 구매 클래스가 아닌 클래스 중 말을 건 현상 P(ㄱT |ㄱB): 구매 클래스가 아닌 클래스 중 말을 걸지않은 현상3. Posterior Probability(사후 확률)
이번엔 Likelihood와 헷갈릴 수 있는 Posterior Probability다. 말 그대로 사후, 일이 벌어진 이후, 해당 클래스일 확률을 말한다.
이 사후확률의 장점은 주관적인 믿음, 신뢰 등을 통계로 활용할 수 있다는 점이다. 사전 확률은 경험에 의해서만 생성될 수 있기 때문에 정량적으로 측정되지 않더라도 이를 예측할 수 있다.
어떤 현상이 관측했을 때, 특정 클래스를 추적한다고 할 수 있다. 위의 예시를 들어보자면, 말을 거는 현상을 거친 사람 중, 물건을 산 사람의 확률이라고 정의한다.
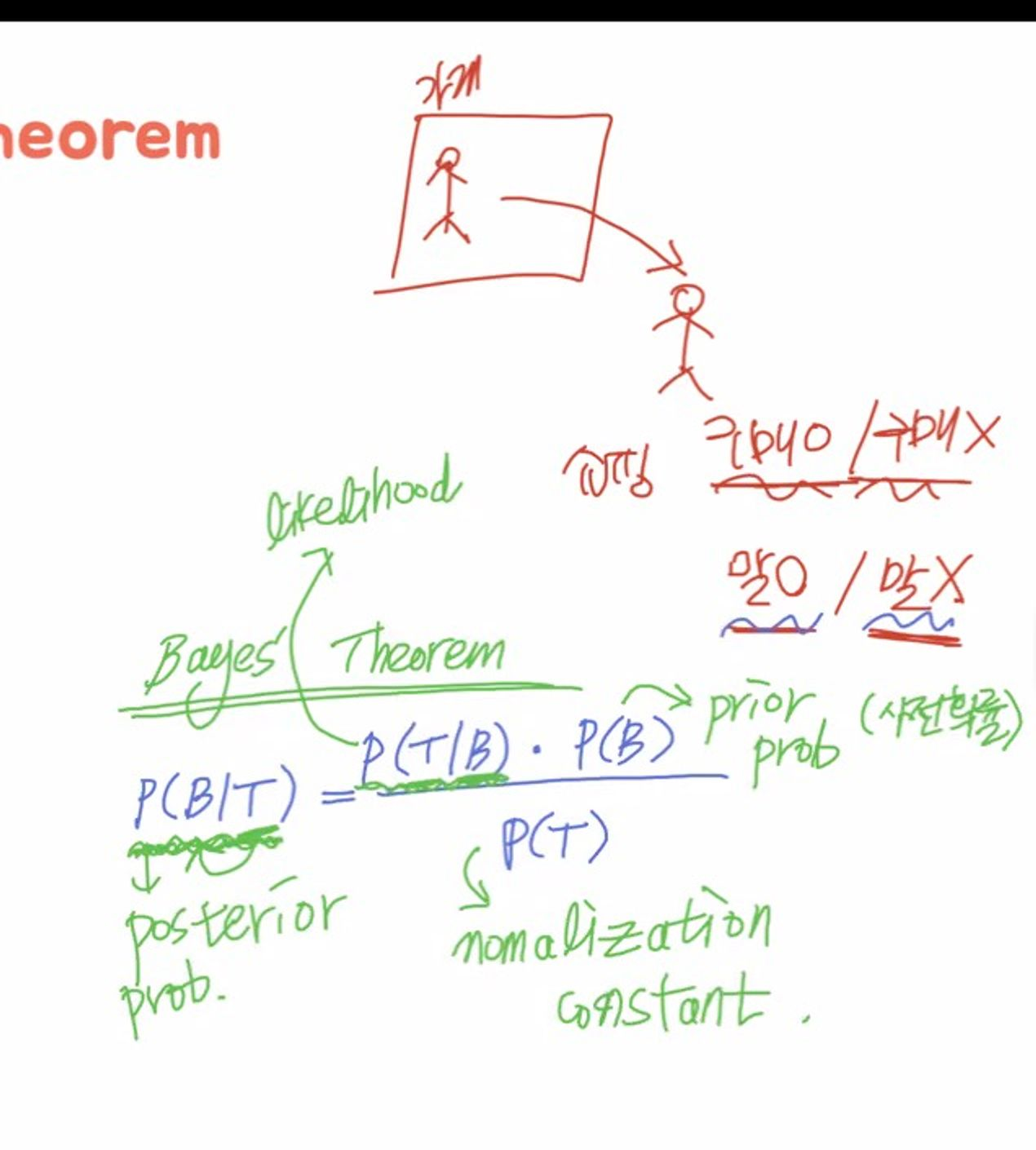
Bayes’ Theorem에서 가장 중요한 내용이기도 한 이 사후확률의 식은 다음과 같다.
💡 **P(B|T) = P(T/B) * P(B) / P(T)**비교적 구하기 쉬운 likehood에 비해 사전 확률은 구하기가 어렵지만, 아래와 같은 정보를 같고 있다면 쉽게 계산할 수 있다.
Likelihood: P(T/B)
Prior Probability: P(B)
Normalization Constant: P(T)
베이즈 정리의 장점은 한정적 자원(데이터)를 통해 많은 현상을 관측할 수 있다는 점이다.
물건을 살 것 같은 고객에게 자원을 투자해야 하며, 어떤 고객의 구매 의지가 있는지 판별을 해야하기에
“구매 고객은 실제로 말을 걸 확률이 높다”라는 정보를 update 해줌으로써 알고리즘을 개선시킬 수 있다.
4. Bayes’ Theorem 실습
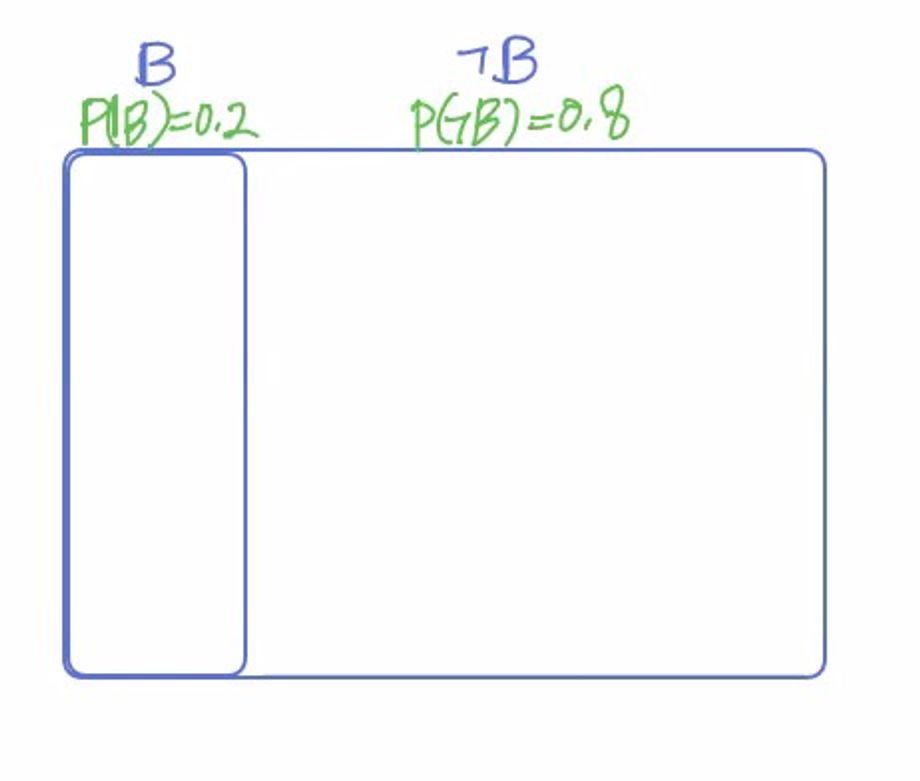
💡 구매의지 O / X → B / ㄱB 말 O / X → T / ㄱT위 내용을 기억하고 실습을 해보자. 구매 확률: 20% / 비구매 확률: 80%이라고 하면 시각화는 다음과 같이 표현이 가능하다. 전체 크기는 1로 잡는다면 위와 같이 범위를 설정할 수 있다.
Likelihood 계산
Likelihood를 계산해보자. P(T |B)를 0.9로 설정한다면 P(ㄱT|B) = 0.1이 될 것이며, P(T |ㄱB)는 0.3이라고 설정한다면 P(ㄱT |ㄱB)는 0.7이 될 것이다. 시각화를 한다면 그림 2와 같아진다.

그림1
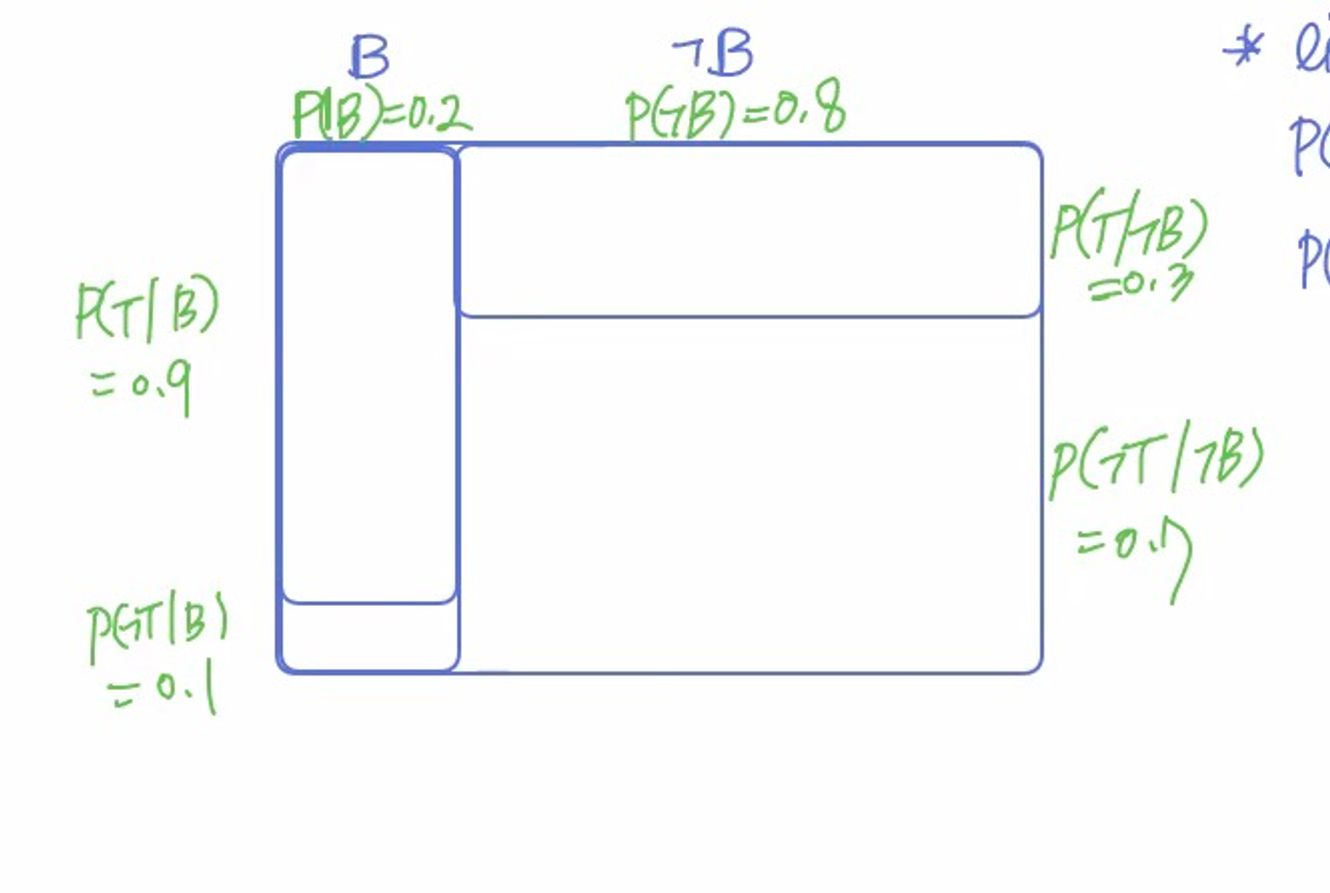
그림2
Join Probability(교집합)
그 다음은 교집합의 확률을 계산해보자. P(T)를 알기 위해선 P(B n T) / P(B n ㄱT)값을 더해야 한다.
해당 범위를 계산해보면 다음과 같다.
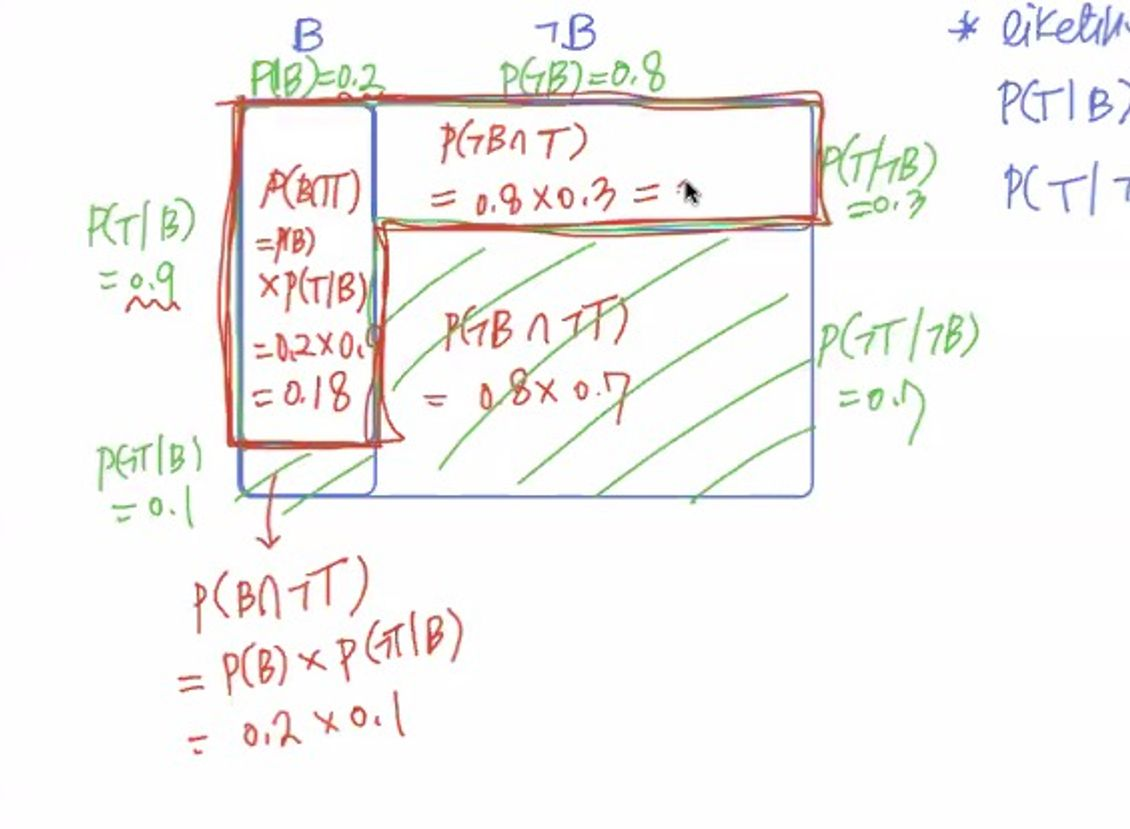
P(B n T): Joint Probability
: P(B) X P(T|B) = 0.2 * 0.9
P(B n ㄱT)
: P(B) X P(ㄱT|B) = 0.2 * 0.1
P(B n ㄱT) = 0.8*0.3
P(ㄱB n ㄱT) = 0.8*0.7
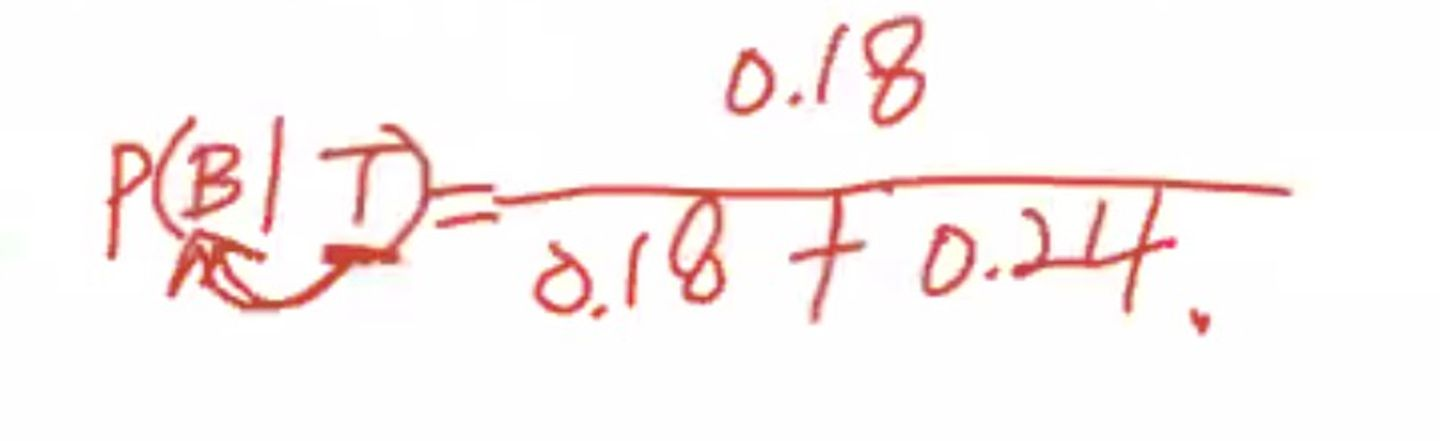
따라서 위 요소들을 계산하면 다음과 같다.

처음에 0.2였던 확률이 0.43으로 업데이트 되었다. 이게 사실상 베이즈 정리라고 할 수 있다.
“말을건다”(결과)를 역추적 → 구매 O / X(원인)을 추정해나가는 과정이 바로 베이즈 정리의 핵심이라고 할 수 있다.
정리
B / ㄱB → hypothesis라고 하며, 분류하고자 하는 의밀 담고 있다
T / ㄱT → evidence라고 하며, 이것에 이용하는 정보라고 할 수 있다.
분류하고자 하는 것 / 이것에 이용하는 정보
LIKELIHOOD
예시) 교실 바닥 → 긴 머리카락 → 여자?
- 사전정보를 통한 경향성 또는 가능성
- MLE(Maximum likelihood Estimation)
사전 정보가 들어온다: 교실의 학생이 긴머리 남학생이라면?
Prior Probability
예시) 긴 머리가 많은 남학생 반: 남학생에게서 온 것이라 판단할 수 있음
- MAP(Maximum A posterior)
- 사전정보 활용을 통한 경향성 파악
즉, Prior(사전정보) + Likelihood(경향성)이 베이즈 정리
돈이 되는 알고리즘
사람이랑 비슷한 알고리즘
즉각적 판단을 기반으로 반응을 이끌어낸다.
*** 새로운 정보가 들어올 때 update가 되는걸 baye’s update라고 할 수 있다
