Pygmalion Dali·2023년 9월 19일

python

목록 보기

4/6

💡 Programming에 가장 필수적 내용

항상 print해보는 것

항상 shape을 뽑아보는 것 → 가장 중요한 내용

프로그래밍을 할 때 가장 중요한 것은 두 가지를 뽑아볼 수 있다. 항상 print해 어떤 오류가 발생했는지 짚어낼 것. 항상 shape를 뽑아내 어떤 구조를 갖고 있는지 파악할 것. 이 점을 유의하고 공부를 해보자.

1. 정규분포와 표준정규분포

정규분포를 표준정규분포로 바꾼다면?

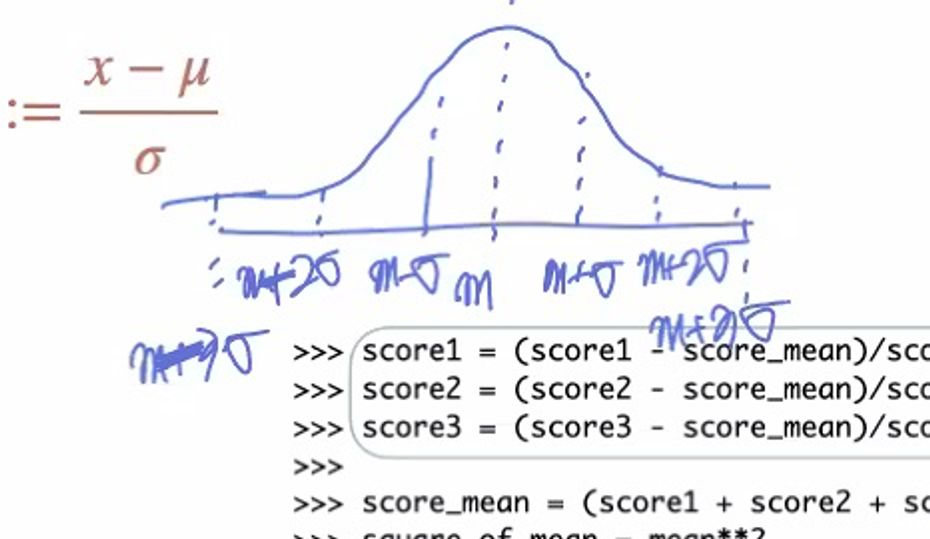
정규분포의 형태의 형태를 표준 정규분포로 바꾼다면 어떤 결과가 나올까?

m이라는 평균값을 정한다면 σ 라는 특정치가 나온다.

|m - σ |: 58퍼

|m - 2σ |: 95퍼

|m - 3σ |: 99퍼

그 이상치에서 벗어난 값은 outlier로 판단하고, 유의미하다 볼 수 없는 데이터가 산출된다.

feature 마다 측정값이 차이가 난다면?

feature 마다 측정값이 차이가 날 때 사용하는 것이 Standardization

이를 진행했을 때 평균은? 0
표준편차는? 1

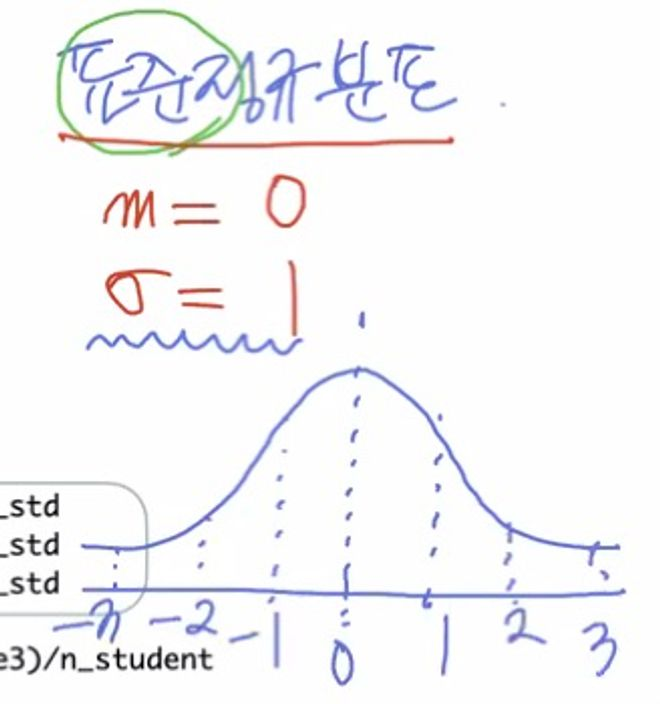
즉, 이렇게 바뀐다는 것이 표준정규분포다.

*참고할 수 있는 함수

np.random.normal: 정규분포에서 랜덤한 값을 뽑아오는 함수

np.random.uniform: 데이터가 분포하는 확률이 모든 범위에서 똑같다 선언해주는 함수

표준편차와 표준정규분포에 대한 지식도 중요하다. 각 벡터의 값은 상이하기 때문에 유사도가 낮을 확률이 매우 높다. 이를 비교하기 위해선 같은 조건이 있어야 한다. 그렇게 하기 위해 표준 편차와 표준정규분포에 대한 지식이 필요하다.

표준편차를 구하면 표준 정규 분포를 따르게 된다
평균이 0 의 값을 갖고, 표준편차가 1이 된다

이를 통해 두 벡터 간의 비교를 진행할 수 있다.

2. 벡터의 구조와 연산

벡터의 개념

벡터란?

오늘은 파이썬을 통해 자료구조의 유형 중 하나인 벡터에 대해 알아볼 것이다. 그렇다면 벡터의 정의란 무엇일까? GPT에게 물어보았다.

불닭볶음면같은 설명으론 내 머리를 이해시킬 수 없으니 초등학생도 이해할 수 있도록 요청했다. 이에 대한 GPT의 답변은 이러하다.

요점을 정리하자면, 벡터란 크기와 양을 지니고 있는 데이터의 유형 중 하나라는 것이다. 친절하게 게임 캐릭터를 예시로 들며 벡터에 대한 이해를 높여주었다.

즉, 벡터의 값은 변수의 수에 따라 달라지며 원점을 통한 거리를 알아볼 수 있다는 것이 특징이었다. GPT의 마지막 말을 보자. 벡터는 크기와 방향을 갖고 있는 숫자의 모음이라는 것을 기억하자.

앞은 벡터의 개념을 배웠다. 그렇다면 이제부터는 벡터 구조를 실제로 연산해보자.연산하려면 어떤 과정을 거쳐야 할까?

벡터 - 벡터 구조의 연산

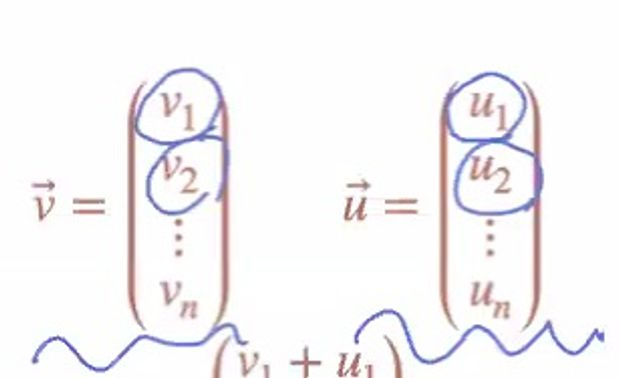
벡터의 표기는 이런 식으로 화살표를 해주면 된다.

벡터는 이런 식으로 선언해서 사칙연산에 적용할 수 있다. 주로 사용되는 차원은 2차원과 3차원으로 구성된다.

x1, y1, z1 = 1, 2, 3
x2, y2, z2 = 3, 4, 5

x3, y3, z3 = x1 + x2, y1 + y2, z1 + z2
x4, y4, z4 = x1 - x2, y1 - y2, z1 - z2
x5, y5, z5 = x1 * x2, y1 * y2, z1 * z2

print(x2, y2, z2)
print(x3, y3, z3)
print(x4, y4, z4)

----

3 4 5
4 6 8
-2 -2 -2

이렇게 벡터의 형태로 결과값이 산출되는 것을 알 수 있다. 우리가 익히 하던 방식과 유사하다는 것을 알 수 있다.

Hadamard Product: 두 벡터를 원소 끼리 곱한 것

뿐만 아니라 이 용어를 기억할 필요가 있다. 하다마드 프로덕트라는 이름을 가진 이 벡터는 매우 단순한 정의를 갖고 있다. 바로 두 벡터를 원소 끼리 곱한 것.

왜 곱셈만 특정 용어로 설명을 했을까? 이유는 실제 업무에서 벡터 간 연산을 가장 많이 하는 것이 ‘곱셈’이기 때문이다. 실제 현업에서 사용하는 것도 곱셈을 통한 벡터 연산이라고 하니, 너무 어렵게 생각하지 말고

“아, 하다마드 프로덕트라는 애는 벡터를 곱해준 형식을 말하는 거구나”라고 생각하면 될 것이다.

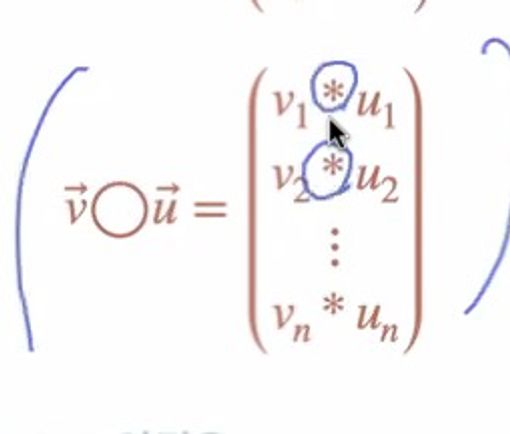
이렇게 두 벡터 사이에 O를 넣으면 벡터 끼리의 연산이라고 표시를 해주는 것이다

최고다 GPT!!!!

Scalar와 Vector의 연산(Broadcasting)

scalar? : 특정한 하나의 수

어렵게 생각할 필요가 없다. 모른다면 GPT에게 물어보면 된다.

그렇다면 질문. 그렇다면 특정 scalar와 vector를 연산할 수 있을까? 답은 ‘모른다’이다.

본래 구조에 의하면 벡터와 스칼라의 연산은 차원이 다르기 때문에 불가능하다. 하지만 python의 numpy 라이브러리의 broadcasting을 통해 다른 차원을 연산이 가능하도록 만들어줄 수 있다.

다음 문제를 같이 풀어보자.

#스칼라의 벡터 구조
a = 10
x1, y1, z1 = 1, 2, 3

x2, y2, z2 = a*x1, a*y1, a*z1
x3, y3, z3 = a + x1, a + y1, a + z1
x4, y4, z4 = a - x1, a - y1, a - z1

print(x2, y2, z2)
print(x3, y3, z3)
print(x4, y4, z4)

----

10 20 30
11 12 13
9 8 7

a=10이라는 특정 변수에 정수를 선언해줬다. 여기서 2,3,4 벡터에 a를 빼고, 더해주고, 곱해주는 과정을 거쳤더니 아래와 같은 결과가 나왔다.

파이썬은 문법에서 비교적 자유로운 언어이기 때문에 이렇게 편하게 연산할 수 있게 되는 것이다. 이 얼마나 편안한 기능인지 모르겠다(라고 배웠다)

벡터 놈

일반적 벡터는 뭐라고 말할까? position vector라고 말한다. 즉, 원점에서 출발하는 벡터라고 이해하면 편하다. 그렇다면 그 벡터의 길이는 뭐라고 책정할까?

벡터 놈이라고 한다. 벡터의 크기를 말한다. 즉 길이를 나타낸다고 할 수 있다. 벡터의 길이는 피타고라스 정리를 통해 정리될 수 있는데, 아래와 같은 식으로 정리할 수 있다.

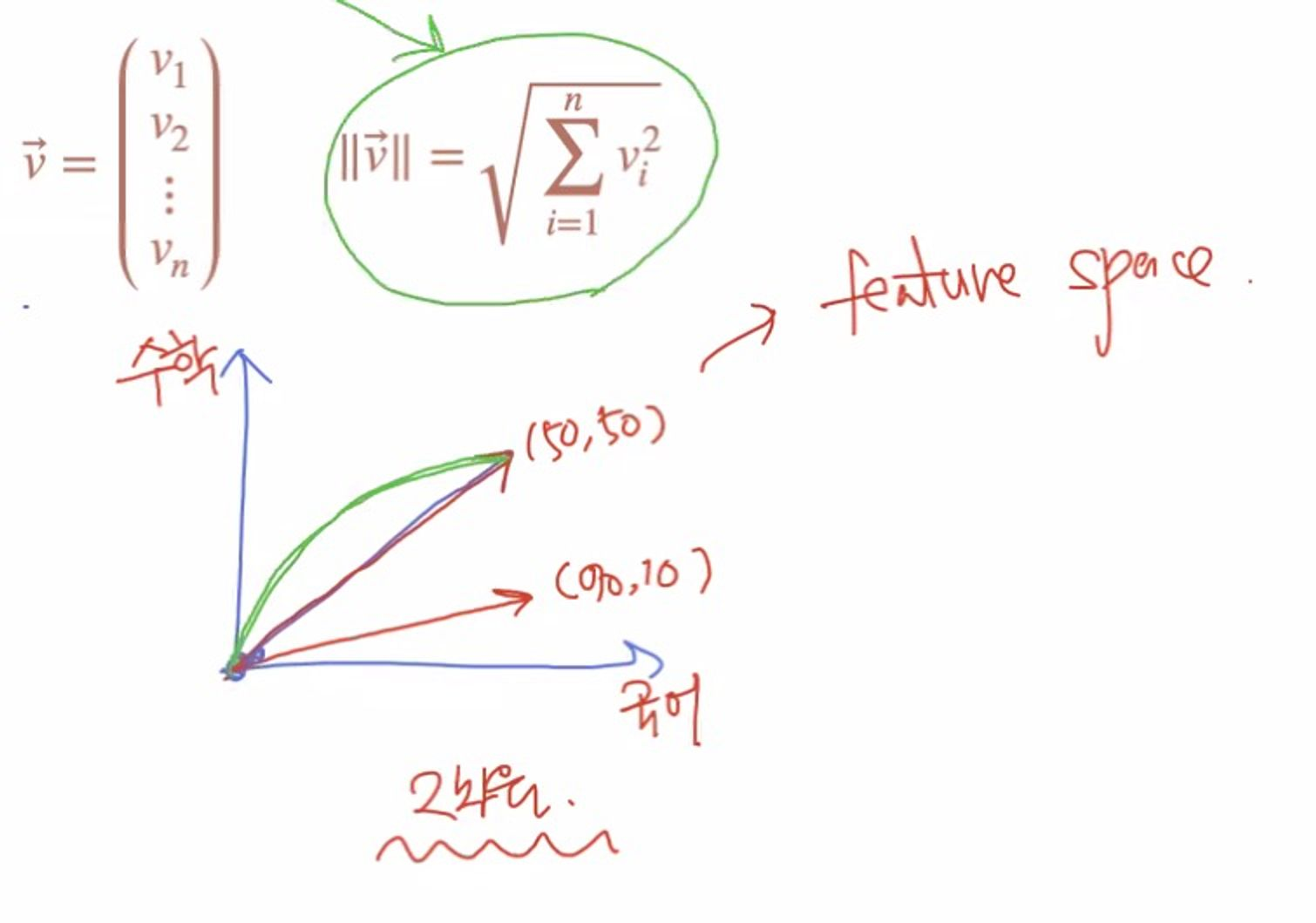
그렇다면, 왜 벡터가 필요할까?

예시를 들어보자 학생 A와 학생B가 있다고 해보자. 국어와 수학 성적을 각각의 feature라고 하며,

벡터를 그려준다면(feature space) 각각 국어축 / 수학축에 그려줄 수 있다.

이론적으로 feature space는 무한대이나, feature 수에 따라 차원이 늘어난다.

유닛 벡터 만들기

unit vector의 크기는 1이다. 나는 그렇게 기억하기로 했다. 1이라는 상수로 정해주는 이유는 값이 다른 벡터 끼리 비교를 해줘야 하기 때문이다. 정규화 과정을 거쳐 유닛 벡터를 정규화 과정을 거치는 것이다.

#유닛 벡터 만들기

x, y, z = 1, 2, 3

norm = (x**2 + y**2 + z**2)**0.5
print(norm) -> 3.7416573867739413

x, y, z = x/norm, y/norm, z/norm
norm = (x**2 + y**2 + z**2)**0.5
print(norm) -> 1.0

위와 같이 norm값은 제곱을 씌워준 합의 루트값이라고 이해를 하면 된다. 그 후에 norm 분의 x,y,z 값을 새로 업데이트 시킨 후, 다시 루트 값을 씌우면 norm 값은 항상 1이다.

내적(Dot Product)

내적은 어떤 의미일까? 두 벡터 간의 유사도를 측정하는 정도로 이해하면 된다.

코사인 세타 값이 커질수록 세타(사잇값)는 작아지고, 두 벡터는 유사하다고 할 수 있다. 즉, 코사인이 높으면 높을수록 기울기가 비슷하다고 이해해도 된다.

정리해보자.

두 벡터가 유사하다

= 비슷한 특성을 지닌다

= 코사인 세타 값이 커진다

= 사잇값(θ)이 작아진다

라고 정리할 수 있다. cosθ(코사인 세타)에 대해서도 알아보자.

cosθ?

-1 ~ 1의 값을 가진다
unit vector
두 유닛의 유사도를 비교할 수 있다
두 벡터 크기 영향력을 없애고 사잇값을 통해 유사도를 확인할 수 있다.

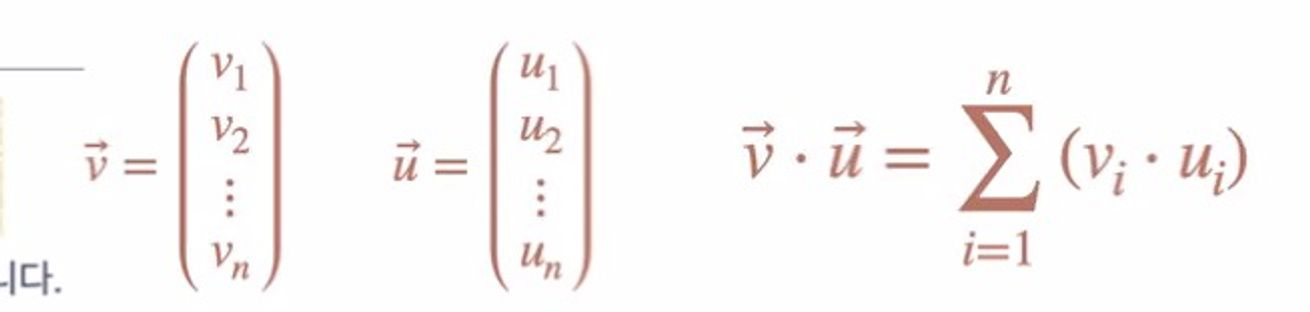
내적의 일반식은 두 벡터의 요소들을 곱해준 것의 총 합이라고 볼 수 있다.

#Dot Product(내적)
x1, y1, z1 = 1, 2, 3
x2, y2, z2 = 3, 4, 5

dot_prod = x1*x2 + y1*y2 + z1*z2
print(dot_prod)

유클리디언 디스턴스

유클리디언 디스턴스는 간단하다. 두 벡터 간의 거리라고 이해하면 된다. 피타고라스 정리를 이용해 벡터의 사이 값을 구해주면 되는 것이다.

두 벡터 간의 거리를 계산하기 위해서 두 개의 벡터 위치 값을 인식하면된다.

가까운 k개의 다수 분류를 확인하는 방법은 무엇일까?

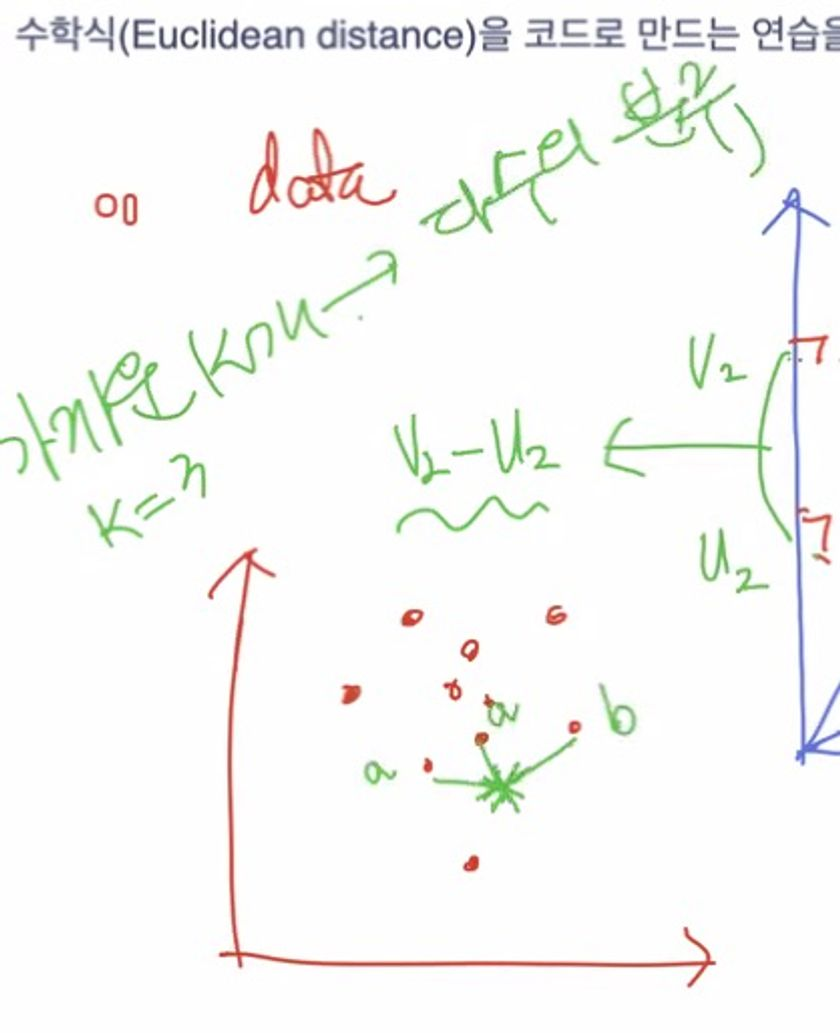
새로운 데이터도 k의 위치가 얼마나 거리가 먼지 다수의 분류를 통해 분석할 수 있다. 예제로 들어가보자.

#유클리디안 디스턴스

x1, y1, z1 = 1, 2, 3
x2, y2, z2 = 3, 4, 5

euclidian_distance = ((x1-x2)**2 + (y1-y2)**2 + (z1-z2)**2)**0.5

#euclidian_distance **= 0.5 = 루트 씌워주기
print(euclidian_distance)

Mean Squared Error

그 다음은 Mean Squared Error이다. 모델 성능 지표 중 하나라고 보면 되는데, 예측치와 얼마나 유사한지 분석할 수 있는 좋은 방법이다. 식을 정리하면 아래와 같다

1/n*\sum_i^n(모델의 예측값 - 결측값)**2

(모델의 예측값 - 정답값)2] / n**

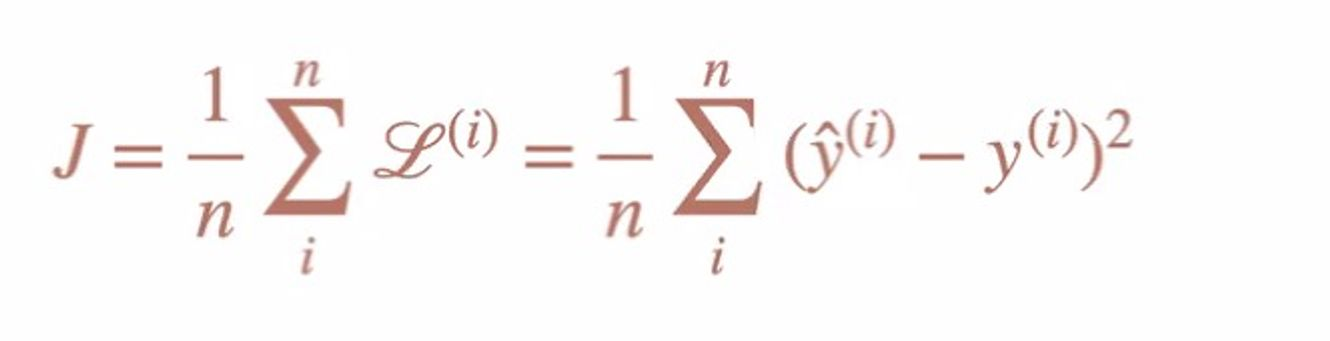
예측치는 hat을 씌워주면 된다

예제로 넘어가보자.

#mean squared error(mse)

#예측치를 선언합니다
pred1, pred2, pred3 = 10, 20, 30

#y값을 생성합니다 & 데이터의 수를 선언합니다
y1, y2, y3 = 10, 25, 40
n_data = 3

#에러 값과 정답값의 차의 제곱을 선언합니다
s_error1 = (pred1 - y1)**2
s_error2 = (pred1 - y2)**2
s_error3 = (pred1 - y3)**2

#MSE를 연산합니다
mse = (s_error1 + s_error2 + s_error3)/n_data
print(mse)