
KMP 알고리즘
커누스 모리스 프랫 알고리즘(Knuth-Morris-Pratt algorithm)
-
완전 탐색(Brute force)의 시간 복잡도 문제를 해결하기 위한 문자열 탐색 알고리즘
길이가 N 인 문자열에서 길이가 M인 문자열을 찾는 과정이라는 가정 하에,
Brute force :
O(N*M)KMP :
O(N+M)
Failure Function, pi
-
찾고자 하는 문자열의 전처리 과정 필요
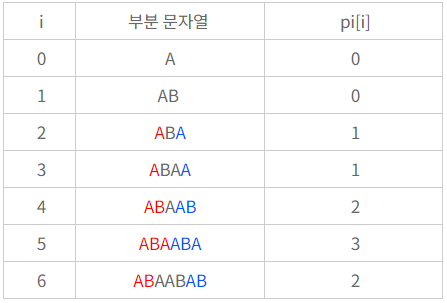
실패 함수(failure function, pi[i])를 만드는 과정
실패 함수: i 번째 위치에서 접두사 == 접미사가 되는 최대 접두사의 길이
https://cantcoding.tistory.com/13 에서 전처리 테이블 사진 참조
Python Code
# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 패턴의 테이블 생성
def KMP_table(pattern):
lp = len(pattern)
tb = [0 for _ in range(lp)] # 정보 저장용 테이블
pidx = 0 # 테이블의 값을 불러오고, 패턴의 인덱스에 접근
for idx in range(1, lp): # 테이블에 값 저장하기 위해 활용하는 인덱스
# pidx가 0이 되거나, idx와 pidx의 pattern 접근 값이 같아질때까지 진행
while pidx > 0 and pattern[idx] != pattern[pidx]:
pidx = tb[pidx-1]
# 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
if pattern[idx] == pattern[pidx] :
pidx += 1
tb[idx] = pidx
return tbKMP
-
Failure Function 에서 만든 테이블을 활용하여 KMP 알고리즘 진행
-
문자열을 확인할 인덱스
idx, 패턴을 확인할 인덱스pidx를 분리하여 활용- 문자열의
idx번째 문자와 패턴의pidx번째 문자가 일치한다면, 두 인덱스를 모두 증가시킴 - 일치하지 않는 경우,
pidx-1값을 앞서 생성한 테이블에 적용하여 얼만큼 생략을 하고 진행할 수 있는지 확인pidx가 0이 되거나, 문자열의idx번째 문자와 패턴의pidx번째 문자가 일치할 때 까지pidx변경
- 문자열의
-
pidx가 패턴의 맨 끝 인덱스에 도달하는 경우가 문자열에서 패턴을 찾은 경우가 됨- 문자열 안에 패턴의 개수가 여러번 나타나는 경우, 이 때의 시작 인덱스를 계산하여 결과 값을 계산하는 리스트에 저장하고,
pidx를 테이블 값 기준으로 하여 변경
https://j2wooooo.tistory.com/119 에서 사진 참조
- 문자열 안에 패턴의 개수가 여러번 나타나는 경우, 이 때의 시작 인덱스를 계산하여 결과 값을 계산하는 리스트에 저장하고,
Python Code
- 해당 패턴이 몇 번 나타나는 지, 그 때의 시작 인덱스가 몇인지를 리턴
- 밑에 써있는 practice 문제를 반영한 코드
def KMP(word, pattern):
# KMP_table 통해 전처리된 테이블 불러오기
table = KMP_table(pattern)
results = [] # 결과를 만족하는 인덱스 시점을 기록하는 리스트
pidx = 0
for idx in range(len(word)):
# 단어와 패턴이 일치하지 않는 경우, pidx를 table을 활용해 값 변경
while pidx > 0 and word[idx] != pattern[pidx] :
pidx = table[pidx-1]
# 해당 인덱스에서 값이 일치한다면, pidx를 1 증가시킴
# 만약 pidx가 패턴의 끝까지 도달하였다면, 시작 인덱스 값을 계산하여 추가 후 pidx 값 table의 인덱스에 접근하여 변경
if word[idx] == pattern[pidx]:
if pidx == len(pattern)-1 :
results.append(idx-len(pattern)+2)
pidx = table[pidx]
else:
pidx += 1
return resultsPractice
- 백준 #1786. 찾기

