[백준 문제 풀이] 2720번 세탁소 사장 동혁

Junu Kim·2025년 7월 6일

Java baekjoon boj

코딩테스트 문제 풀이 (백준, HackerRank)

목록 보기

10/46

[2720] 세탁소 사장 동혁

난이도: ★☆☆☆☆ • solved on: 2025-07-06

문제 요약

문제 유형: 구현, 그리디
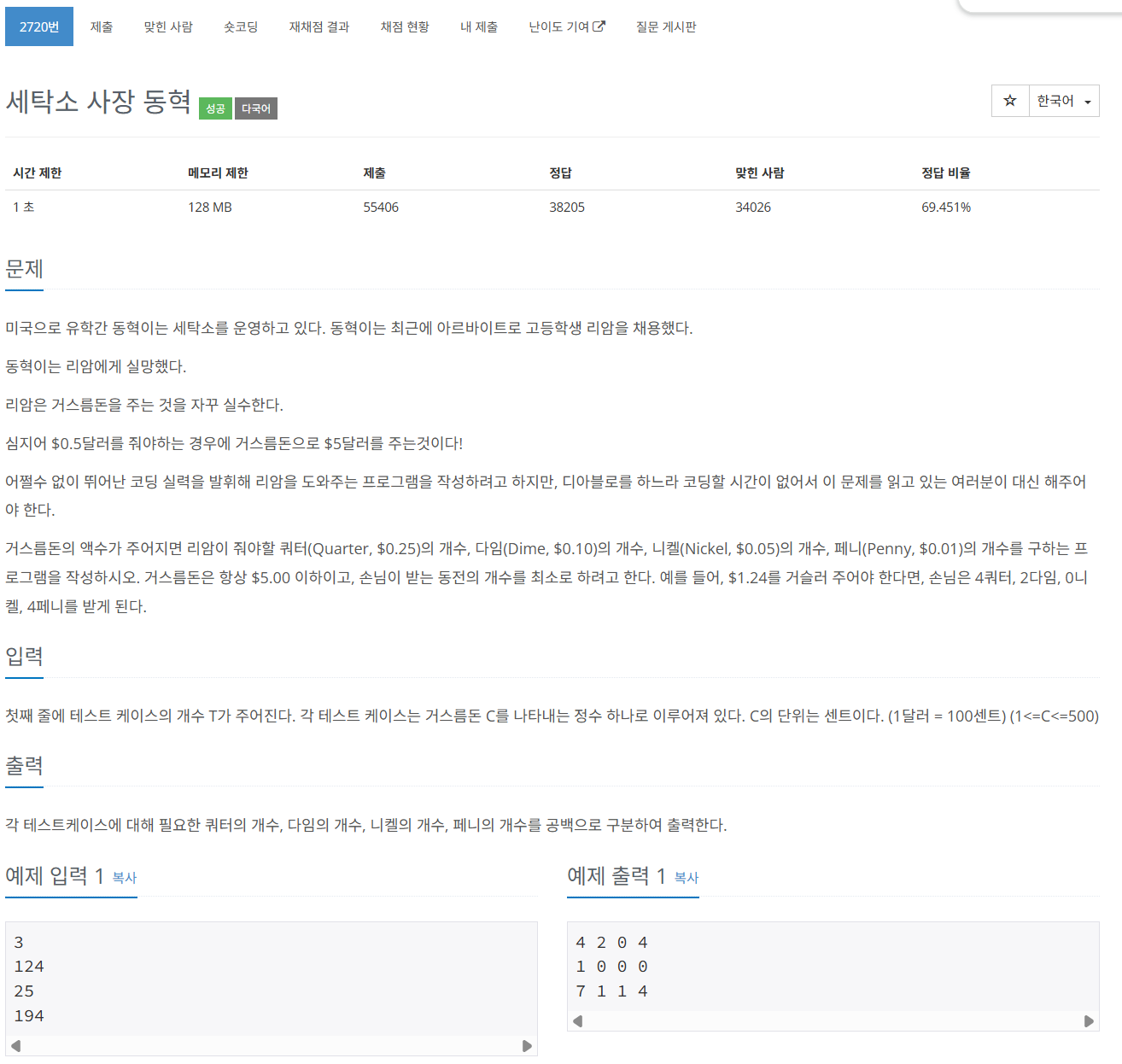
요구사항: 거스름돈 금액이 주어질 때, 미국 동전(쿼터 25¢, 다임 10¢, 니켈 5¢, 페니 1¢) 별로 최소 개수로 나누어 출력해야 한다.

사용 개념

자료구조
- 단순 변수(int) 사용
알고리즘/기법
- 그리디(Greedy): 큰 단위 동전부터 차례대로 나눔
핵심 키워드
- 동전 교환, 몫/나머지 연산, 반복문

풀이 아이디어 및 코드

방법 1: 입력값 순차 처리, 각 동전별 몫 연산

문제 분해

입력받은 거스름돈을 25, 10, 5, 1 단위로 차례차례 나눈다.

각 동전별 몫을 구해 사용 개수를 결정하고, 남은 금액을 갱신한다.
핵심 로직 흐름
for (테스트케이스 수만큼 반복) {
    쿼터 = 남은돈 / 25;
    남은돈 -= 쿼터 * 25;
    다임 = 남은돈 / 10;
    남은돈 -= 다임 * 10;
    니켈 = 남은돈 / 5;
    남은돈 -= 니켈 * 5;
    페니 = 남은돈 / 1;
    남은돈 -= 페니;
}
예외 처리

금액이 0이면 모두 0 출력

import java.util.*;
import java.lang.*;
import java.io.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int change = 0;
        int quarter = 0;
        int dime = 0;
        int nickel = 0;
        int penny = 0;
        for (int i = 0; i < n; i++) {
            change =  Integer.parseInt(br.readLine());
            quarter = change / 25;
            change -= quarter*25;
            dime = change / 10;
            change -= dime*10;
            nickel = change / 5;
            change -= nickel*5;
            penny = change / 1;
            change -= penny;
            System.out.println(quarter+" "+dime+" "+nickel+" "+penny);
        }
    }
}

방법 2: 배열과 반복문으로 개선

동전 단위 배열 활용

동전의 단위를 배열로 선언: {25, 10, 5, 1}

동전 수 계산 결과도 배열에 저장

반복문으로 처리

for-each문을 이용하여 반복적으로 연산 수행

코드 간결화 및 동전 종류 추가·수정시 용이

입출력 최적화

StringBuilder를 활용하여 출력문 성능 개선 가능

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int t = Integer.parseInt(br.readLine());
        int[] coins = {25, 10, 5, 1};

        while (t-- > 0) {
            int change = Integer.parseInt(br.readLine());
            StringBuilder sb = new StringBuilder();
            for (int coin : coins) {
                sb.append(change / coin).append(" ");
                change %= coin;
            }
            System.out.println(sb.toString().trim());
        }
    }
}

시간·공간 복잡도

방법 1/2 공통

시간 복잡도: O(T) (T = 테스트 케이스 수, 각 케이스마다 상수 연산)
공간 복잡도: O(1)

어려웠던 점

몫(/)과 나머지(%) 연산자를 헷갈려서 오답을 냈다.

배운 점 및 팁

반복문 + 배열 활용으로 코드가 더욱 간결해지고, 동전 종류가 바뀌어도 쉽게 확장할 수 있다.
잔돈 문제의 기본 구조를 확실히 익혀두면, 변형 문제가 나와도 쉽게 응용할 수 있다.
그리디(Greedy) 접근법이 동전 교환 문제에 유용했다.
(단, 동전 단위가 '배수 관계'일 때만 항상 최적)
그리디 알고리즘 (Greedy Algorithm)

: 현재 상황에서 가장 좋아 보이는 선택 (최선의 선택, local optimum)을 반복해서 전체 해답에 도달하는 방식의 알고리즘이다. 즉, 한 단계에서 최적이라고 판단되는 것을 즉시 선택하면서, 전체적으로도 좋은(최적) 해답에 도달하는 것을 목적으로 한다.
1. 주요 특징
- 지역적으로 최적(local optimum) 선택만 고려한다.
- 미래의 상황(전역적 최적값, global optimum)까지 고려하지 않고, 매 순간의 선택에만 집중
- 구현이 매우 쉽고, 실행 속도도 빠름
- 항상 최적해를 보장하지는 않음
  (단, 동전 문제처럼 ‘특정 조건’이 맞을 때는 항상 최적해 가능)
1. 대표 예시 문제
- 동전 거스름돈 문제 (미국 동전처럼 단위가 배수 구조일 때)
- 최소 신장 트리 (MST) (Kruskal Algorithm, Prim's Algorithm)
- 다익스트라 (Dijkstra Algorithm, Shortest Path Problem)
1. 그리디 알고리즘의 성립 조건
  1. Greedy Choice Property (그리디 선택 속성)
    : 매 순간 가장 좋아 보이는 선택을 해도, 이후의 선택에 영향을 주지 않고 (독립 관계) 전역적 최적해 (Global Optimum) 에 도달할 수 있는 구조여야 한다.
    : 각 단계에서 현 시점에서 가장 최선의 선택만 반복하면 전체 해답도 최선이 된다.
  1. Optimal Substructure (최적 부분 구조)
    : 전역적 최적해 (Global Optimum)가, 지역적 최적해 (Local Optimum)로부터 구성될 수 있어야 한다.
    : 문제를 쪼갠 작은 문제에서도 항상 각각의 최적해가 전체의 최적해로 연결된다.
  만약 둘 중 하나라도 성립하지 않으면, 동적 프로그래밍(DP) 같은 더 복잡한 방법이 필요할 수 있다.

차이점 (그리디 vs DP)

그리디: 한 번 선택한 것은 다시 바꾸지 않음. 미래를 고려하지 않고, 매 순간 최선만 고름.

DP: 각 단계에서 모든 선택의 경우를 다 고려해서, 나중에 필요하면 이전 선택을 바꾸기도 함. 최적해를 항상 보장
참고 링크 : Wikipedia - Greedy algorithm

참고 및 링크

문제 링크: https://www.acmicpc.net/problem/2720
참고 블로그/깃허브: https://en.wikipedia.org/wiki/Greedy_algorithm

추가 연습 문제

비슷한 유형 (GPT 추천) :
- [5585] 거스름돈 (https://www.acmicpc.net/problem/5585)
- [11047] 동전 0 (https://www.acmicpc.net/problem/11047)
확장 문제 (GPT 추천) :
- 임의 동전 단위에서 동전의 최소 개수 구하기 (DP 응용)
- 동전 교환 방법의 가짓수 구하기 (DP)