
Today I Learned
[Solidity]
오늘은
string=>structmapping,string=>array[]mapping과 길이가 고정된 배열에서 요소를 추가하는 방식, 그리고 for문 작성하는 법과 머클 패트리샤 트라이에서 노드가 나뉘는 과정과 라딕스 트라이에 대해 배웠다.
array & struct 복습
// 생략
function getAllList() public view returns(D[] memory) {
return D_list;
}
function getList(uint _n) public view returns(D memory) {
return D_list[_n-1];
}위 코드 위에
구조체 D가 있고D형 배열 D_list가 있을 때 배열의 모든 정보를 반환하는 함수와 특정 데이터만 반환하는 함수이다.
이 때 중요한 점은 각각 함수가 반환하는 타입이 다르다는 것인데,
전체 배열을 반환하는 함수는 반환하는 타입도 배열이기 때문에D[] memory로 작성해야하고,
특정 데이터만 반환하는 함수는구조체 D이기 때문에D memory로 작성한다.
mapping
contract MAPPING {
struct Student{
uint number;
string name;
string[] classes;
}
mapping(string => Student) Teacher_Student;
mapping(string => Student[]) Teacher_Class;
function setTeacher_Student(string memory _Teacher,uint number,string memory name,string[] memory classes) public {
Teacher_Student[_Teacher] = Student(number,name,classes);
}
function getTeacher_Student(string memory _Teacher) public view returns(Student memory) {
return Teacher_Student[_Teacher];
}
function setTeacher_Class(string memory _Teacher, uint _number, string memory _name, string[] memory _classes) public {
Teacher_Class[_Teacher].push(Student(_number, _name, _classes));
}
function getTeacher_Class(string memory _Teacher) public view returns(Student[] memory) {
return Teacher_Class[_Teacher];
}
}위 코드에서는 string=>Student, string=>Student[] 로 각각 매핑해주었다.
그 후 선생님 이름을 넣으면 학생의 이름과 수업정보, 번호를 가진 구조체의 값들을 부여하고 반환하는 함수, 그리고 선생님 이름을 넣으면 선생님이 가르치는 모든 학생의 구조체 값들을 push하고 반환하는 함수를 작성했다.
두 함수가 비슷하지만 중요한 점은setTeacher_Student는 key-value값으로 부여해주면 되지만,setTeacher_class함수는 value값이 배열이기 때문에push를 해준다는 점이다.
fiexdArray
contract fixedArray {
uint[] a;
uint[4] b;
function getALength() public view returns(uint) {
return a.length;
}
function pushA(uint _n) public {
a.push(_n);
}
function getA() public view returns(uint[] memory) {
return a;
}
function getBlength() public view returns(uint) {
return b.length;
}
function pushB(uint n, uint _n) public {
b[n] = _n;
}
function getB() public view returns(uint[4] memory) {
return b;
}
uint count;
function pushB2(uint _n) public {
b[count++] = _n;
}
function pushB3(uint _n) public {
b[++count] = _n;
}
function getCount() public view returns(uint) {
return count;
}
}위 코드에서는 a라는 동적 배열과 b라는 정적 배열을 선언한 후 a와 b의 길이, 요소 추가, 배열 반환 하는 함수를 작성하였다.
여기서의 중요한 점은 동적 배열 a에는 push를 하여 요소를 추가하였지만, 정적 배열 b에는 배열의 인덱스와 요소의 값을 입력받아 추가하였다는 점이다.
정적 배열은 길이가 고정되어 있기 때문에push, pop을 할 수 없다.
그렇기 떄문에 길이가 4라면 0~3인덱스 사이에 요소만 변경할 수 있다.
그리고 아래에count라는 숫자형 변수를 선언하였다.
그 후 count값 즉, 인덱스 값인데,count++는후위 증가 연산자로 _n 값을 b 배열에 추가 한 후 count를 1 증가 시킨다.
따라서 b[0]에 _n 값을 저장한 후에 count가 1이 되기 때문에 정상적으로 인덱스 0부터 _n이 추가된다.
하지만++count는전위 증가 연산자로 count가 1 증가한 후 _n값을 배열에 저장한다.
그렇기 때문에 인덱스 1부터 저장되기 때문에 인덱스 0은 그대로 0인채 저장된다.
맞다 그리고 중요한 점!!! 배열의 크기가 정적이어도 반환하는 타입에는memory도 써줘야 한다!!!!
for문
contract ForLoop {
function forLoop() public pure returns(uint){
uint a;
for(uint i=1; i<6; i++) {
a = a+i; // a+=i
}
return a;
}
function forLoop2() public pure returns(uint, uint){
uint a;
uint i;
for(i=1; i<6; i++) {
a = a+i;
}
return (a,i);
}
function forLoop3() public pure returns(uint, uint) {
uint a;
uint i;
for (i=1; i<=5; i++) {
a += i;
}
return (a, i);
}
uint[4] c;
uint count;
function pushA(uint _n) public {
c[count++] = _n;
}
function getA() public view returns(uint[4] memory) {
return c;
}
function forLoop4() public view returns(uint) {
uint a;
for (uint i=0; i<4; i++) {
a = a + c[i];
}
return a;
}
function forLoop5() public view returns(uint) {
uint a;
for (uint i=0; i<c.length; i++) {
a += c[i];
}
return a;
}
uint[] d;
function pushD(uint _n) public {
d.push(_n);
}
function getD() public view returns(uint[] memory) {
return d;
}
function forLoop6() public view returns(uint) {
uint a;
for (uint i=0; i<d.length; i++) {
a += d[i];
}
return a;
}
}for문은 c언어에서의 for문과 똑같은 것 같다.
for () -> 괄호안에는 타입과 시작점을 함께 써주고, 끝점, 그리고 변화방식이다.
머클 트리
- 이진 트리 형태이다.
- 대표적으로 블록체인에서는 머클 루트를 생성할 때 사용한다.
- 머클 루트를 통해 효과적으로 자료의 변형 인식이나 검증 과정을 수행해낼 수 있다.
- SPV노드가 풀 노드에게 확인할 때도 사용된다.
- 이더리움에서는 수정된 머클 트리, 머클 패트리샤 트리를 사용한다.
머클 패트리샤 트리
- 트리를 사용하는 근본적인 이유는 저장, 수정, 삭제, 검색을 효율적으로 할 수 있기 때문이다.
- 총 4가지 종류(State, Storage, Transactions, Receipts)의 머클 패트리샤 트리가 사용된다.
- 노드에는 총 4가지 노드(Blank, Extension, Branch, Leaf)가 있다. 여기서의 노드는 트리 안의 노드이다.
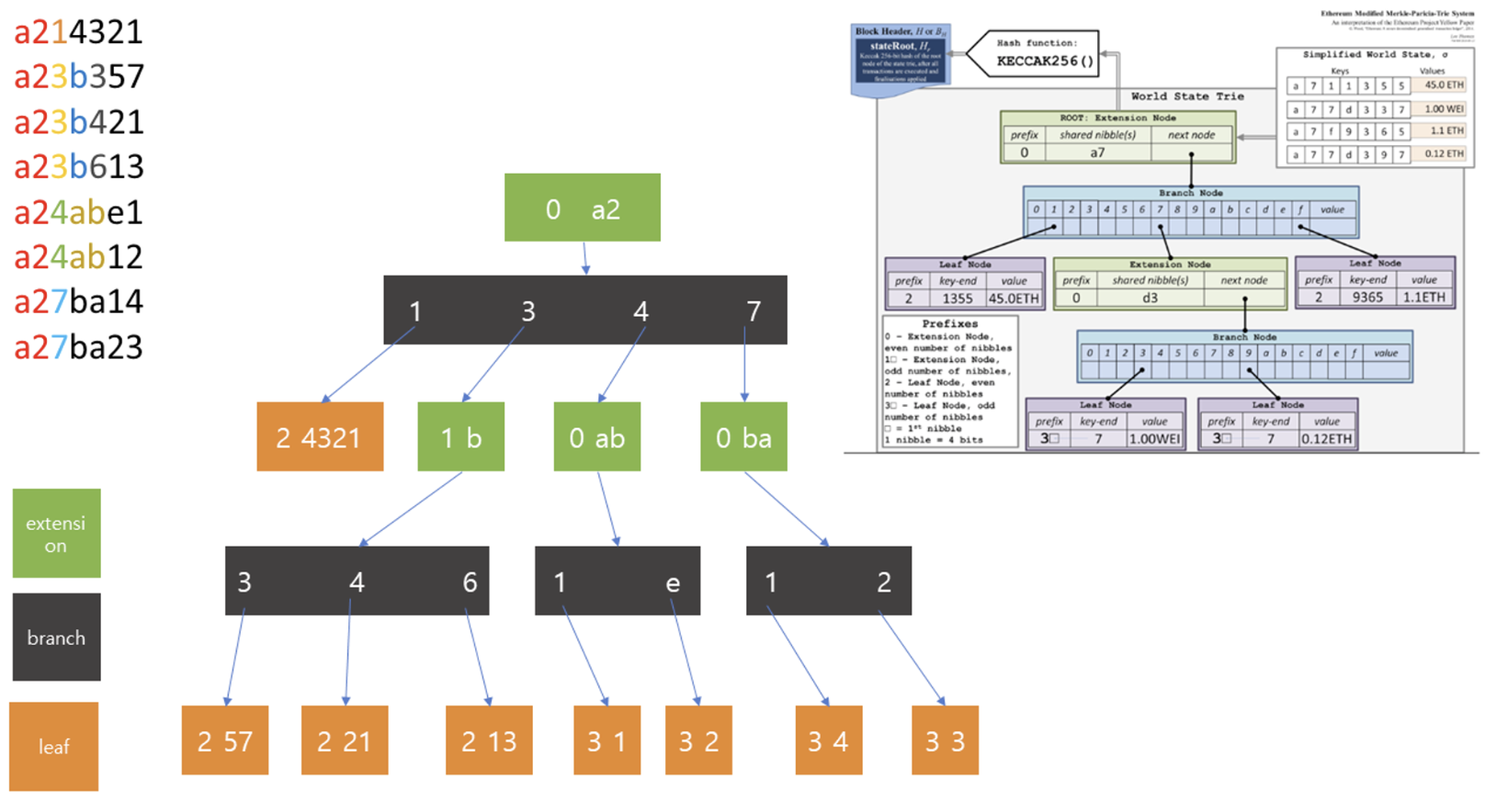

바로 위 사진은 접두사가 표현되는 부분인데 해석을 해보면,
0: extension node 이면서 key 값이 nibble의 갯수로 따졌을 때 짝수인 경우
1: extension node 이면서 key 값이 nibble의 갯수로 따졌을 때 홀수인 경우
2: leaf node 이면서 key 값이 nibble의 갯수로 따졌을 때 짝수인 경우
3: leaf node 이면서 nibble의 갯수로 따졌을 때 홀수인 경우
반면에 Radix trie는 중복되는 부분을 하나의 노드로 표현하여 불필요한 부분을 제거하여 효율성을 높인다.