H-Index level 2 자바

🧫 문제 분석

✔️ 출처

H-Index level 2

📖 문제

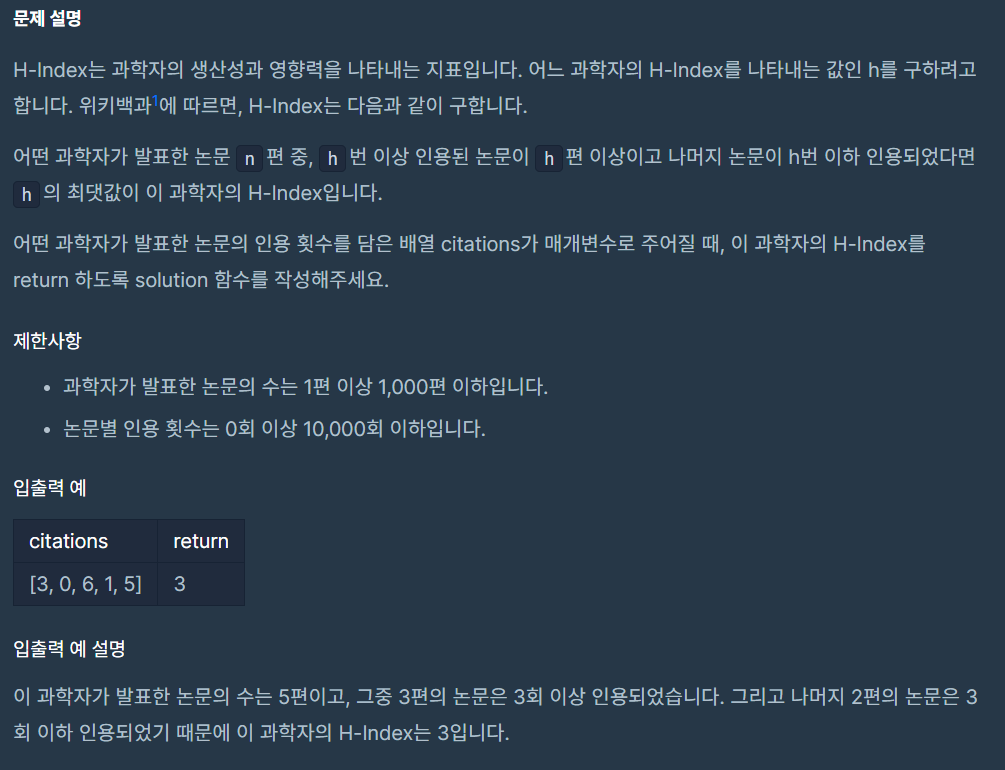
문제를 잘 못 이해해서 삽질했다.
n편 중 h 번 이상 인용된 논문이 h편 이상이고,
나머지 논문은 개수에 상관없이 h 번 이하 인용되었다면 h의 최댓값이 H-Index이다.

---

🔅 문제 풀이

import java.util.Arrays;

class Solution {
    public int solution(int[] citations) {
        Arrays.sort(citations);
        int max = 0;
        
        // i = 논문 인용 횟수
        for (int i = 0; i < citations[citations.length - 1]; i++) {
            int count = 0;
            // 인용횟수 h 이상인 논문 카운트
            for (int j = 0; j < citations.length; j++) {
                if ( i <= citations[j]) count++;   
            }
            // 인용횟수 h이상인 논문이 h편 이상인지 판별
            if (i <= count) max = i;
            else break;
            
        }
        
        // n편중 h번 이상이 h 개 이상, 나머지는 h번 이하 인 h의 최댓값

        return max;
    }
}

흠.. 느리다.

프로그래머스 좋아요 1등 풀이

import java.util.*;

class Solution {
    public int solution(int[] citations) {
        Arrays.sort(citations);

        int max = 0;
        for(int i = citations.length-1; i > -1; i--){
            int min = (int)Math.min(citations[i], citations.length - i);
            if(max < min) max = min;
        }

        return max;
    }
}

이해 해보기

예제 [1,1,1,7,8,10] 이고 정답은 3이다.

결국에는 citations 길이 안에서 결정이 난다. 왜냐하면 h 개 이상의 논문이 있어야하기때문이다.

쉽게 보자면
10 이상 인용된 논문의 개수 : 1
8 이상 인용된 논문의 개수 : 2
7 이상 인용된 논문의 개수 : 3
...

citations의 요소가 인용된 횟수이며, 그 횟수 이상이 논문의 개수여야한다.
인용횟수와 논문 개수중 더 작은 것을 찾아내고 그 중에서 최댓값을 선정한다.

---

❗ 오답노트 / 필요한 지식

1. 저런 발상을 하는 연습이 필요한 것 같다...
2. 내가 짠게 뭔가 이해가 더 잘되는 것 같다. 풀이는 내가하던대로 하되 나중에 더 최적화해야겠다 싶을 때 분석해서 코드를 리팩토링하는게 맞는 것 같다.