문제 설명

세로선의 갯수 N과 가로점선의 갯수 H가 주어진다.그리고 이미 놓여진 사다리의 갯수 M도 주어진다.
이때, 최대 3개의 사다리를 더 배치해서, 모든 i에 따라 i세로선이 사다리게임을 따라 i세로선에 도착할 수 있는 경우에 그 최소로 더 놔야하는 사다리의 갯수를 구해라. 불가능한 경우는 -1을 출력해라.
또한, 사다리는 수평선상에서 연속해서 배치할 수 없다.
시간제한 2초, 메모리 512mb

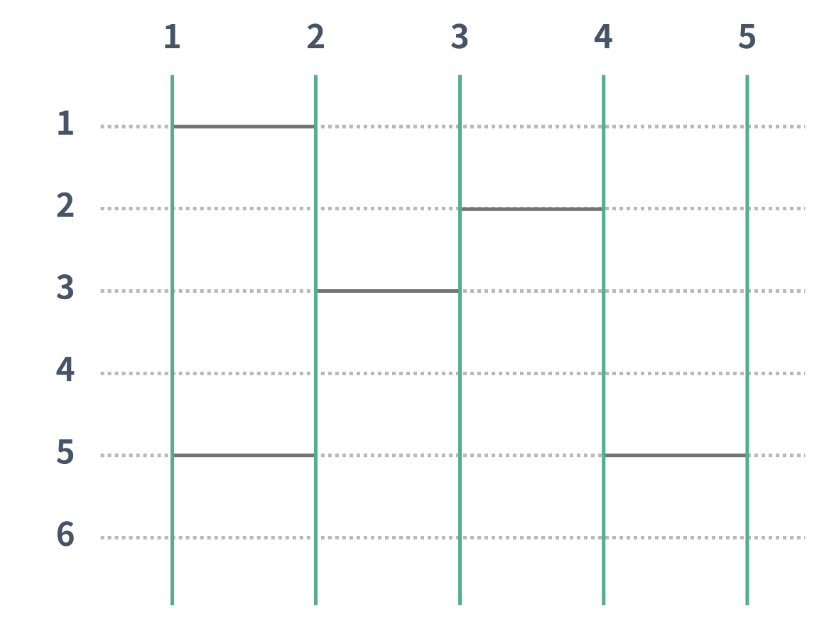
아래의 예시는 N이 5, H가 6, M(미리 놓여진 사다리의 갯수) 5인 경우이다.

문제 접근 및 세 가지 실수들

처음에 문제를 제대로 안읽어서, 조합으로 풀면 무조건 시간초과가 날텐데 어떻게 하라는건지 감이 안잡혔다. 하지만, 문제에 최대 3개까지만 배치할 수 있다고 해서, 조합(dfs)+브루트포스의 구현문제라고 확신했다.

구현 문제를 풀면서 내가 이렇게 실수를 많이 할 줄 몰랐다. 총 세 개의 실수를 했다...

• 첫 번째 실수: 문제가 우리가 평소에 풀던 대로 N이 행을 의미하는게 아니라 열을 의미하는 값이여서 자꾸 조건식을 N이랑 H를 반대로 쓰는 등 좀 헤맸다.

• 두 번째 실수: 내가 시간을 줄이기 위해 사다리를 배치할 수 없는 위치들을 저장하는 unableToAdd 라는 불리언 배열을 놨다. 그런데, dfs에서 배치가능한 사다리면 배치한 다음 dfs호출 전에 unableToAdd[x][y]를 true로 하고, dfs를 마치고 돌아오면 다시 이걸 false로 해버려서 문제가 생겼다. 생각해보면 꼭 이번 그 사다리 때문이 아니라 이미 기존에 true였다면 그 사다리가 제거된다고 해서 false로 돌릴 필요가 없다는 것임.
  그래서 아래와 같은 로직이 dfs에 존재한다.

                int leftSideY = y - 1;
                int rightSideY = y + 1;
                boolean isLeftAlreadyCanNotAdd = false;
                boolean isRightAlreadyCanNotAdd = false;

                if (leftSideY >= 1) {
                    if (unableToAdd[x][leftSideY]) isLeftAlreadyCanNotAdd = true;
                    unableToAdd[x][leftSideY] = true;
                }
                if (rightSideY < N) {
                    if (unableToAdd[x][rightSideY]) isRightAlreadyCanNotAdd = true;
                    unableToAdd[x][rightSideY] = true;
                }
                isLadderPlaced[x][y] = true;
                dfs(total, remain - 1, x, y);
                isLadderPlaced[x][y] = false;
                if (leftSideY >= 1 && !isLeftAlreadyCanNotAdd) unableToAdd[x][leftSideY] = false;
                if (rightSideY < N && !isRightAlreadyCanNotAdd) unableToAdd[x][rightSideY] = false;

• 세 번째 실수: 답이 0이 안나올 것이라고 착각하고 말았다. 즉, 입력 데이터 그 자체가 이미 정답인 경우는 더이상 사다리를 배치안해도 되므로 답이 0이다. 그런데, 나는 1~3까지만 조합의 갯수를 시도하고 모두 실패하면 -1을 출력했다.

문제풀이

import java.util.*;
import java.io.*;

class Main {
    static int N, H;
    static int M;
    static boolean[][] isLadderPlaced;
    static boolean[][] unableToAdd;
    static int answer = -1;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        H = Integer.parseInt(st.nextToken());
        isLadderPlaced = new boolean[H + 1][N + 1];
        unableToAdd = new boolean[H + 1][N + 1];

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int x = Integer.parseInt(st.nextToken());
            int y = Integer.parseInt(st.nextToken());
            isLadderPlaced[x][y] = true;
            int leftSideY = y - 1;
            int rightSideY = y + 1;
            if (leftSideY >= 1) unableToAdd[x][leftSideY] = true;
            if (rightSideY < N) unableToAdd[x][rightSideY] = true;
        }

        if (M == 0) {
            System.out.println(M);
            return;
        }

        for (int i = 0; i <= 3; i++) {
            dfs(i, i, 1, 0);
            if (answer != -1) break;
        }
        System.out.println(answer);
    }

    // 해당 위치 이후부터 남은 갯수
    static void dfs(int total, int remain, int cx, int cy) {
        if (remain == 0) {
            if (isAllStoS()) answer = total;
            return;
        }

        int x = cx;
        if (cy == N - 1) x = cx + 1;
        for (; x <= H; x++) {
            int y = 1;
            if (x == cx) y = cy + 1;
            for (; y < N; y++) {
                if (unableToAdd[x][y] || isLadderPlaced[x][y]) continue; // 얘는 추가할 수 없다고 명시되어있는 녀석이거나, 이미 추가된 녀석이면
                int leftSideY = y - 1;
                int rightSideY = y + 1;
                boolean isLeftAlreadyCanNotAdd = false;
                boolean isRightAlreadyCanNotAdd = false;

                if (leftSideY >= 1) {
                    if (unableToAdd[x][leftSideY]) isLeftAlreadyCanNotAdd = true;
                    unableToAdd[x][leftSideY] = true;
                }
                if (rightSideY < N) {
                    if (unableToAdd[x][rightSideY]) isRightAlreadyCanNotAdd = true;
                    unableToAdd[x][rightSideY] = true;
                }
                isLadderPlaced[x][y] = true;
                dfs(total, remain - 1, x, y);
                isLadderPlaced[x][y] = false;
                if (leftSideY >= 1 && !isLeftAlreadyCanNotAdd) unableToAdd[x][leftSideY] = false;
                if (rightSideY < N && !isRightAlreadyCanNotAdd) unableToAdd[x][rightSideY] = false;
            }
        }
    }

    static boolean isAllStoS() {
        for (int i = 1; i <= N; i++) {
            if (!isStoS(i, 0, i)) return false;
        }
        return true;
    }

    static boolean isStoS(int s, int x, int y) {
        if (x == H) return y == s;

        if (y < N && isLadderPlaced[x + 1][y]) {
            return isStoS(s, x + 1, y + 1);
        } else if (y > 1 && isLadderPlaced[x + 1][y - 1]) {
            return isStoS(s, x + 1, y - 1);
        } else {
            return isStoS(s, x + 1, y);
        }
    }
}

구현 문제를 풀때는 조건식과 예외를 잘 설계해야할 것 같다. 이건 디버깅 기능 없이 프로그래머스였으면 풀기 힘들었을 것 같다...