문제 접근

문제를 읽어보면, 시작 위치부터 도착지점까지 이동할 수 있는 정해진 경로 중 가장 짧은 거리를 구하는 것이다.
-> 이것만 봐도 일단 bfs라는 것은 알 수 있다.
하지만, 이 문제의 진짜 문제는 정해진 경로를 구하는 것이다.

정해진 경로란, 이 문제에서 사각형들을 좌표위에 쌓아올렸을 때 만들어지는 최외곽 테두리를 말한다.
이 테두리를 구하는 과정을 정말 노가다로 조건식으로 찾으려고 하면 너무 복잡하다.

결국, 이 문제의 핵심은 도형을 순차적으로 쌓아올리면서 다음과 같은 과정으로 map을 색칠해줘야 한다.
나는 여기서 테두리는 2, 사각형 내부는 1, 아무것도 아니면 0으로 했다.

• 사각형의 모든 좌표를 일단 이중 포문으로 돌린다.
• 이미 1로 색칠되어 있다면, 이는 이전에 쌓아진 사각형의 내부라는 의미로, 내가 이번에 쌓아올리는 사각형의 테두리 영역이라고 하더라도 최외곽 테두리가 아니라서 의미 없다.
• 아직 색칠된 영역이 아니라면, 테두리 좌표면 2로, 그냥 일반 내부 좌표면 1로 색칠한다.

그리고, 이 문제에서 bfs를 돌리기 위해 주의사항으로 모든 좌표의 개념을 두 배로 해주어야 한다. 안그러면, bfs로 돌리다가 의도치 않게 옆에 있는 사각형의 테두리로 이동할 수 있기 때문이다.

아래 예시는 대충 그린 것이라 사실 문제에서는 주어지지 않는 모양이지만, 참고용으로 느낌만 알면 될 것 같다.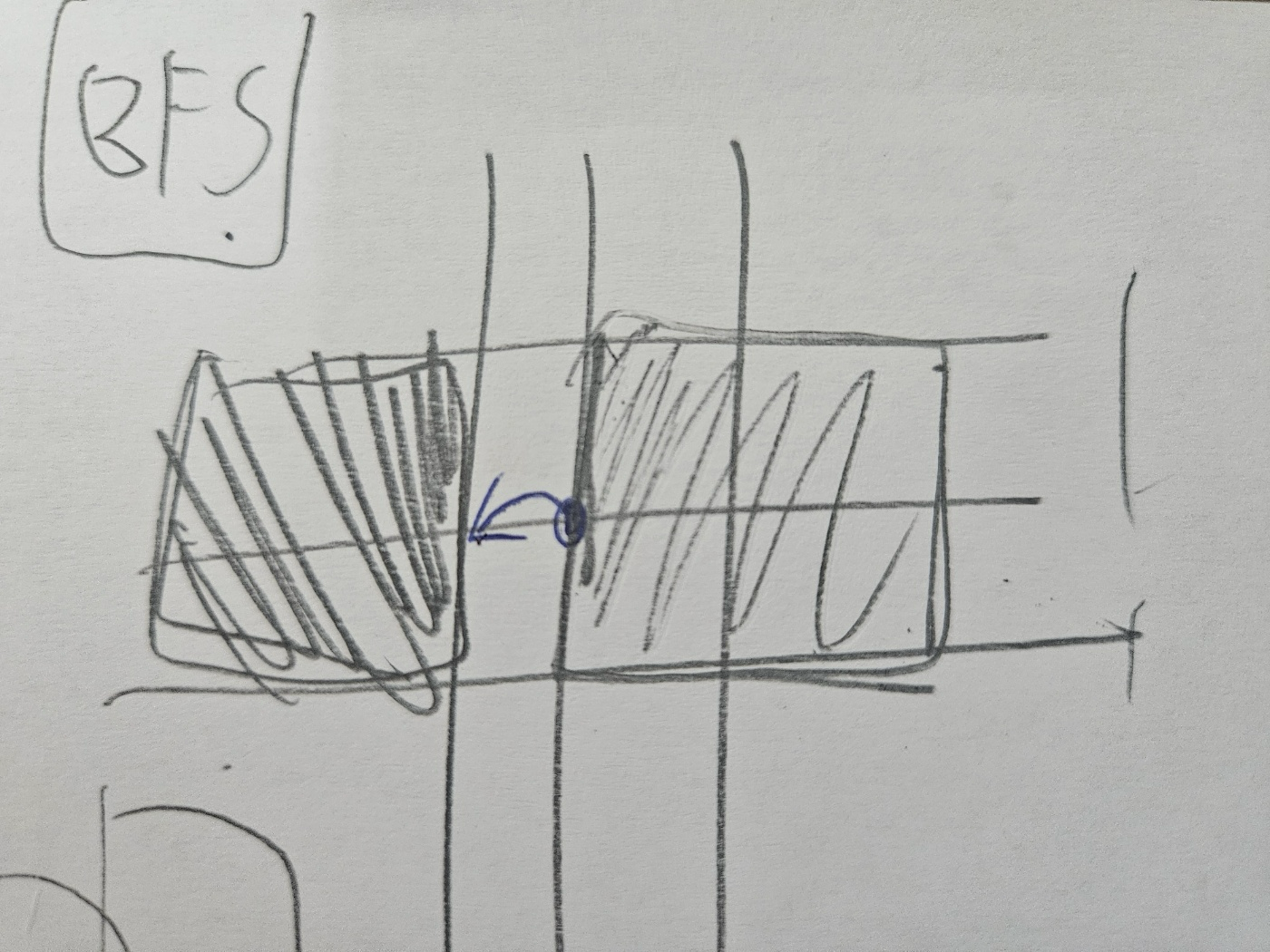위 예시에서 파란 화살표로 이동하면 안된다.
이를 방지하기 위해, 모든 좌표 개념을 두 배로 만들어서, 테두리 간 거리도 2로 만들면 bfs를 돌리는데 방해받지 않으며, 나온 결과를 나누기 2만 해주면 된다.

문제 풀이

import java.util.*;

class Solution {
    static int[][] map;
    static int N;
    static int[] dx = {0,1,0,-1};
    static int[] dy = {1,0,-1,0};
    public int solution(int[][] rectangle, int characterX, int characterY, int itemX, int itemY) {
        int answer = 0;
        map = new int[101][101]; // 옆에 사각형 녀석으로 bfs타고 가는 것을 방지하기 위해 두 배로 만든다.
        N = rectangle.length;
        for(int i=0; i<N; i++) {
            int lx=2*rectangle[i][0];
            int ly=2*rectangle[i][1];
            int rx=2*rectangle[i][2];
            int hy=2*rectangle[i][3];
            for(int x=lx; x<=rx; x++) {
            for(int y=ly; y<=hy; y++) {
                if (map[x][y] == 1) continue; // 이미 이전 사각형의 내부였다면, 테두리로 칭하지 않음.
                map[x][y] = 1;
                if (x==lx || x==rx || y==ly || y==hy) {
                       map[x][y] = 2; // 테두리인 경우는 2로 칠함.
                }
            }
        }
        }
        
        int iX = itemX*2;
        int iY = itemY*2;
        int cX = characterX*2;
        int cY = characterY*2;
        LinkedList<Node> q = new LinkedList();
        q.add(new Node(cX, cY, 0));
        map[cX][cY] = 0;
        boolean isFind = false;
        while(!q.isEmpty() && !isFind) {
            Node curNode = q.poll();
            for(int i=0; i<4; i++) {
                int nextX = curNode.x + dx[i];
                int nextY = curNode.y + dy[i];
                if (isIn(nextX, nextY) && map[nextX][nextY]==2) {
                    q.add(new Node(nextX, nextY, curNode.d + 1));
                    map[nextX][nextY] = 0;
                    if (nextX == iX && nextY == iY) {
                        answer = (curNode.d + 1) / 2;
                        isFind = true;
                        break;
                    }          
                }
            }
        }
        
        
        return answer;
    }
    
    static boolean isIn(int x, int y) {
        return x>=0 && x<=100 && y>=0 && y<=100;
    }
}

class Node {
    int x;
    int y;
    int d;
    Node(int x, int y, int d) {
        this.x = x;
        this.y = y;
        this.d = d;
    }
}