문제 설명

수평선이 주어진다. 시작 출발 위치는 0이고, 도착지점은 distance로 주어진다. 그리고 이 수평선 위에 바위들이 존재한다. 그리고 이 바위들 중 임의의 n개를 제거한 케이스들의 사이 거리의 최솟값들 중 최댓값을 구해야 한다. 이부분이 살짝 설명이 힘든데, 그냥 그림으로 보면 이해하기 쉽다.

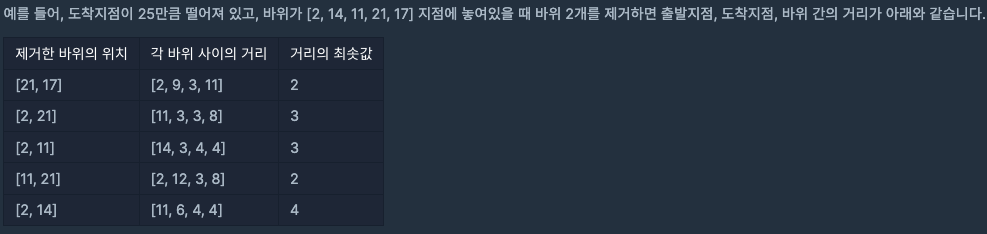
위 케이스에서 답은 4가 된다.

문제 접근

일단 바위는 최대 5만개가 주어진다. 이중 조합을 구하려고 하면, 말도 안되는 수많은 케이스들이 나온다. 또한 각 조합을 구한다고 하더라도, 거리는 최대 10억이다. 즉, 이 문제는 완전탐색으로는 말도안되는 수많은 연산이 필요하다.
보통 이런 수가 매우 크게 주어지고 거리 혹은 길이와 개념으로 수평선에 표현 가능한 문제라면, 이분탐색을 고려해야 한다.

문제를 다시 바라봐야 한다.
생각해보면 모든 조합을 구하고 고려해야 할 필요가 없다. 우리는 최소거리값을 먼저 정하고, 이 최소거리값을 만족하기 위해 바위들을 제거시키면 된다.
그리고 바위들을 제거했는데 n개가 넘는 경우는 최소거리값을 좀 줄여야 할 필요가 있다는거다.

풀이

import java.util.*;

class Solution {
    int answer = 0;
    public int solution(int distance, int[] rocks, int n) {
        Arrays.sort(rocks);
        int l = 1;
        int h = distance;
        int mid = 0;
        while(l<=h){
            mid = (l+h)/2;
            int curMin = distance;
            int count = 0;
            int lastPosition = 0;
            boolean isFailed = false;
            for(int i=0; i<rocks.length; i++) {
                if(rocks[i]-lastPosition < mid) {
                    count++; // 바위 제거했다
                } else {
                    curMin = Math.min(curMin, rocks[i]-lastPosition);
                    lastPosition = rocks[i];
                }
                
                if (count > n) {
                    h = mid - 1;
                    isFailed = true;
                    break;
                }
            }
            
            // 마지막 거리를 아직 측정안했음.
            if(!isFailed) {
                if (distance - lastPosition < mid) {
                    count++;
                } else {
                    curMin = Math.min(curMin, distance-lastPosition);
                }
                
                if(count > n) {
                    h = mid-1;
                } else {
                    answer = Math.max(answer, curMin);
                    l = mid+1;
                }
            }
        }
        
        return answer;
    }
}

추가 설명

                } else {
                    answer = Math.max(answer, curMin);
                    l = mid+1;
                }

이 부분은 왜 필요할까? 우리가 구하는 것은 최솟값을 만족하는 것들 중 최댓값을 구해야 하기 때문이다. 때문에 조건을 만족한다면 더 큰 가능성을 알아봐야 하므로 위와 같은 코드가 존재하는 것이다.