1. 문제

33. Search in Rotated Sorted Array

Medium

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Input: nums = [1], target = 0
Output: -1

2. 문제 해석

오름차순으로 정렬된 정수 배열 번호(별도의 값)가 있습니다.

함수로 전달되기 전에 nums는 알 수 없는 피벗 인덱스 k(1 < = k < nums.length)에서 회전하여 배열이 nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]이 될 수 있습니다.
예를 들어, [0,1,2,4,5,6,7]은 피벗 인덱스 3에서 회전하여 [4,5,6,7,0,1,2]가 될 수 있다.

가능한 회전 후 배열 번호와 정수 대상이 주어지면 대상의 인덱스를 숫자로 반환하고, 숫자가 아닌 경우 -1로 반환합니다.

O(log n) 런타임 복잡도를 가진 알고리즘을 작성해야 합니다.

2.1 Example

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

3. 접근 방법

배열이 알 수 없는 피벗에서 회전할 가능성이 있으므로 이진 검색을 직접 적용할 수 없다. 회전을 처리하기 위해 약간의 수정이 필요하다. 여기서 중요한 점은 두 개의 반쪽 중 하나는 정렬되어야 하고 다른 반쪽은 피벗을 포함해야 한다는 것이다. 예를 들어 배열이 [4,5,6,7,0,1,2]인 경우 왼쪽 절반 [4,5,6,7]은 정렬되고 오른쪽 절반 [0,1,2]에는 피벗이 포함된다. 배열이 [7,0,1,2,4,5,6]인 경우 오른쪽 절반 [2,4,5,6]이 정렬되고 왼쪽 절반 [7,0,1]에 피벗이 포함된다.

따라서 이진 검색의 각 반복에서 먼저 왼쪽과 중간 요소를 비교하여 어느 절반이 정렬되었는지 확인한다. 그런 다음 왼쪽 및 중간 요소와 비교하여 타겟이 정렬된 절반에 있는지 확인한다. 정렬된 절반에 있으면 평소와 같이 해당 절반에서 검색한다. 정렬된 절반에 속하지 않으면 피벗이 포함된 나머지 절반에서 검색한다.

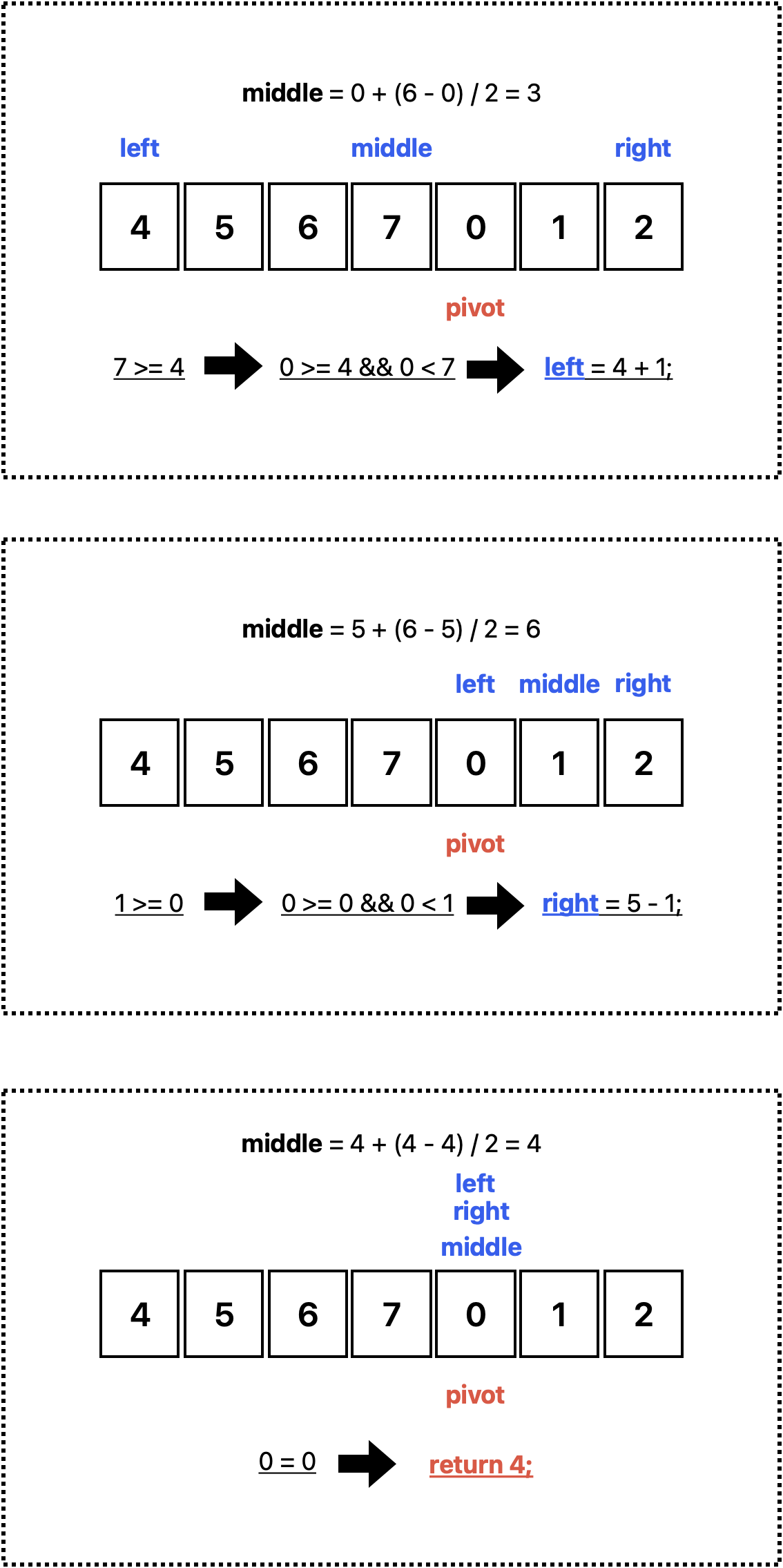
예를 들어 배열이 [4,5,6,7,0,1,2]이고 타겟이 0인 경우이다.

• 왼쪽 = 0, 오른쪽 = 6으로 시작합니다. 중간 인덱스는 3이고 중간 요소는 7입니다.
• 왼쪽 절반 [4,5,6,7]이 정렬되고 오른쪽 절반 [0,1,2]에 피벗이 포함되어 있음을 알 수 있습니다.
• 목표 0이 4, 7과 비교하여 왼쪽 절반에 있는지 확인합니다. 0 < 4 < 7이므로 그 절반에 있지 않습니다.
• 따라서 왼쪽 = 중간 + 1 = 4로 설정하여 피벗이 포함된 오른쪽 절반에서 검색합니다.
• 대상을 찾거나 검색 공간이 모두 소진될 때까지 이 과정을 반복합니다.

3. 의사 코드

배열의 0번째 인덱스부터 시작할 왼쪽 선언;
배열의 마지막 인덱스부터 시작할 오른쪽 선언;

while (왼쪽 < 오른쪽) {
		중간 = 왼쪽 + (오른쪽 - 왼쪽) / 2;
		
		if (배열의 절반이 target과 같다면) {
				중간값 리턴;
		} else if (배열의 절반 기준으로 좌측에 값보다 크다면) {
				if (target이 좌측 인수값 보다 크고 같고, target보다 중간 인수값이 크다면) {
						오른쪽 = 중간- 1;
				} else {
						왼쪽 = 중간 + 1;
				}
		} else if (배열의 절반 기준으로 우측 값이 더 크다면) {
				if (target이 중간 인수값보다 크고, target보다 오른쪽 인수값이 크다면) {
						좌측 = 중간 + 1;
				} else {
						오른쪽 = 중간 - 1;
				}
		}
}

값을 찾지 못했다면 -1 반환;

5. 문제 풀이

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        
        while (left <= right) {
            int mid = left + (right - left) / 2;

            // 절반으로 나누었을 때 찾고자 하는 값이라면
            if (nums[mid] == target) {
                return mid;

            // 왼쪽 절반에 있는지 확인
            } else if (nums[mid] >= nums[left]) {
                // 피벗이 왼쪽 절반에 있다면
                if (target >= nums[left] && target < nums[mid]) {
                    // 왼쪽 절반으로 이분
                    right = mid - 1;
                } else {
                    // 오른쪽 절반으로 이분
                    left = mid + 1;
                }
            // 오른쪽 절반에 있는지 확인
            } else if (nums[mid] <= nums[right]) {
                if (target >= nums[right] && target < nums[mid]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        // 값을 찾지 못했다면
        return -1;
    }
}