우리가 3D세상을 만들기 위해서 가장 중요한 부분 중 하나가 빛이라고 볼 수 있다.
왜냐면 실제 세상에서도 빛을 통해서 물체를 보고, 음영이 있기에 입체적으로 볼 수 있는 것이다.
우리가 만드는 3D세상도 동일하다. 빛으로 인해 어떤 부분이 더 밝아보이고, 어두워보이고, 보이지 않는 등 현실 세계와 비슷하게 돌아갈 수 있도록 만들어야 조금 더 멋진 3D세상을 만들 수 있을 것이다.
오늘은 그런 빛에대한 부분들을 알아보도록 하자.

조명

우선 Direct3D에서 빛이라는 게 어떤 성분들이 있고, 어떻게 작용하는지 알아 볼 필요가 있다.
대표적으로 주변광(Ambient Light), 난반사(Diffuse Reflection), 정반사(Specular Reflection)가 있다.

이 세 성분은 3D 세상에서 물체의 픽셀마다 작용하여 각 성분의 값에 따라 픽셀의 색을 변경한다.
그렇게 되면 우리가 해당 물체를 화면으로 볼 땐 동일한 빨간색이라도 좀 더 어두운 빨간색이 될수도 있고, 밝은 빨간색이 될 수도 있다.

이 성분들을 계산하기 위해선, 반사가 되는 기준을 정해야 하는데 그 기준은 Surface Normal이라는 단위 벡터이다. (이하 노말벡터)
이 노말벡터는 한 점에 접하는 평면과 수직인 벡터이며 이 노말벡터는 모든 픽셀마다 구해야 하지만 레스터라이저 단계에서 정점들을 보간해서 노말벡터를 생성하기에 우리는 폴리곤의 각 정점에 대한 노말벡터만 계산해주면 된다.
물론 Vertex shader에서 조명을 계산해주면 레스터라이저 단계에서 내부 픽셀의 색을 보정하기 때문에 모든 픽셀에 대한 계산을 하지 않아도 된다. 그렇기 때문에 특별히 결과물의 큰 차이가 나지 않는다면 픽셀의 색상 계산을 레스터라이저 단계에 맡기는 것도 최적화의 방법 중 하나이다.

주변광(Ambient Light)

빛은 사실 단 한번만 반사하는 것이 아니라 물체에 반사되고 또 반사되어서 주변의 밝기를 조절한다.
그렇기 때문에 밤에도 충분히 앞을 볼 수 있는것이고, 방에서 플래쉬를 켜면 방 전체가 어느정도 밝아지는 것이다.
하지만 3D세계에서 이런 모든 반사들을 계산할 순 없다. 레이트레이싱 기법이 있지만 아직 온전히 모든 계산을 하는 게 아닌 다양한 기법을 섞어서 표현하고 있을 뿐이다.
그렇기 때문에 기본적으로 보장되는 빛인 ambient를 섞어주는 것이고 이 값은 빛의 최저값을 정해서 아예 보이지 않는 것을 방지하는 값인 것이다.
그래서 최종 색상을 계산할 때 색상 값 + {0.1, 0.1, 0.1} 이런 식으로 값을 더하게 될 것이다.

난반사(Diffuse Reflection)

Diffuse는 표면으로 들어온 빛이 반사 될 때, 표면의 각도에 따라 빛이 퍼지게 되는 것을 말한다.

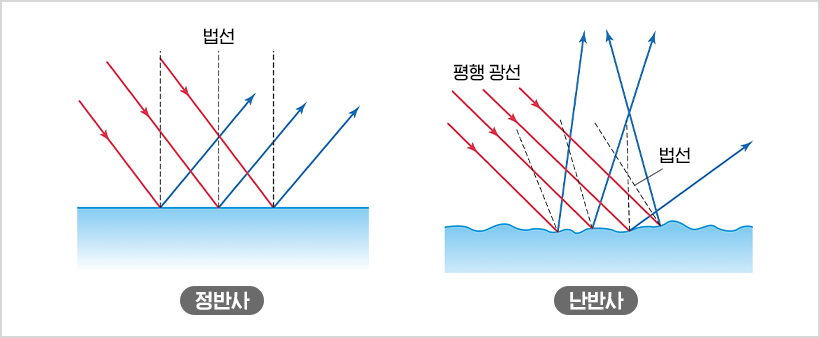
출처 - [호기심 과학] 선명한 화면이 생명, 디스플레이의 표면 관리는 어떻게? (feat.정반사와 난반사)

우선 계산하기 전에 우리는 계산을 단순화 하기 위해서 빛이 진입한 각도에 따라서 빛이 분산되어 반사한다고 가정하고, 빛이 반사되는 정도는 그 재질에 따라서 난반사 값을 다르게 준다. 예를들어 금속에 대한 Material을 만들 때 diffuse값을 {0.7, 0.7, 0.7}으로 줬다면 나무에 대한 값은 {0.2, 0.3, 0.2} 이렇게 주고 계산을 할 수도 있는 것이다.

그래픽에서 이런 재질과 상호작용을 계산할때는 빛이 표면 위쪽으로 고르게 흩어진다고 가정하고 계산하기 때문에 빛의 흩어짐에 따라 물체의 색상을 계산한다.
그렇기 때문에 난반사에 대한 물체의 색상값은 카메라의 위치완 무관하게 단순히 diffuse값과, 물체의 색상, 분산되어 흩어지는 값 이 세 가지로만 계산한다.

여기서 분산되어 흩어지는 값은 람베르트 코사인 법칙이라는 것을 통해서 계산된다.

람베르트 코사인 법칙

빛은 일정한 방향으로 나아가는 광자들의 집단으로 생각할 수 있는데 이 광자는 어느정도의 에너지(빛의 에너지)를 갖고있는데 빛이 1초에 방출하는 총 에너지를 복사선속(radiant flux)이라고 부른다.
조명에서 중요한건 이 방사속의 밀도, 즉 복사조도(irradiance)인데 그 이유는 이 복사조도가 물체의 밝기를 결정하는데 중요한 요소이기 때문이다.

아래를 보자.

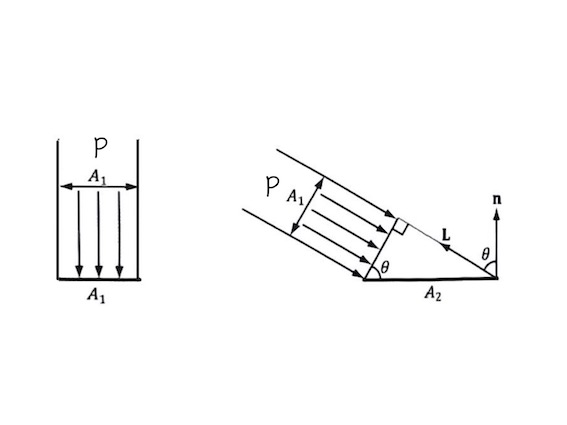
A1과 그 빛을 통과하는 복사선속 P가 있다고 가정했을 때 A1에 해당하는 복사조도 E1 = P/A1이고, A2에 해당하는 복사조도 E2 = P/A1이다.
여기서 A1에 해당하는 빛의 다발을 회전해서 오른쪽과 같이 방향을 바꿨을 때 A1과 A2의 관계는 다음과 같이 된다.
cosθ = A1/A2 -> 1/A2 = cosθ/A1
이때 A2와 수직인 N벡터가 있다고 했을 때 다음과 같은 식이 나온다.
E2 = P/A2 = (cosθ * P)/A1 = E1cosθ = E1(N·L)

간단하게 결과를 말하자면 A2에 해당하는 복사조도는 빛의 방향이 수직인 A1에 cosθ를 곱한것과 같다는 말이며 이 것을 람베르트의 코사인 법칙이라고 한다.

다시 난반사

이제 이 내용들을 종합해보면 난반사를 계산하는 법은 빛의 세기가 P, diffuse값 D, 빛의 방향단위벡터 L, 픽셀의 노말벡터 N이 있을 때 다음과 같이 될 것이다.
P·(D(-L·N))
여기서 잘 보면 L이 아니라 -L이다. 그 이유는 우리가 빛을 계산할 때 방향이 아래 그림과 같이 좌상단에서 우하단으로 간다고 계산하기 때문이다.

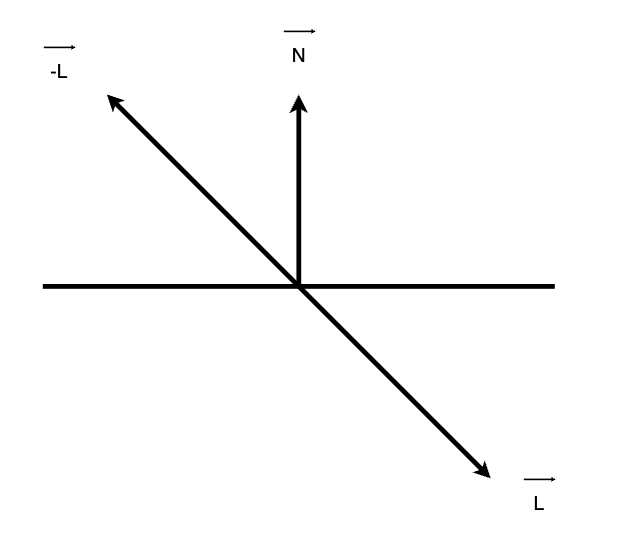
그래서 -L과 N을 내적하면 우리가 원하는 코사인 값이 나오기에 L이 아닌 -L을 내적하게 되는 것이다.

정반사(Specular Reflection)

Specular는 간단하게 말하면 하이라이트다. 물체에서 빛이 반사되어 우리 눈에 비칠 때 그 부분은 하얗게 빛나는 걸 볼 수 있는데 그 정도를 계산해주게 될 것이다.

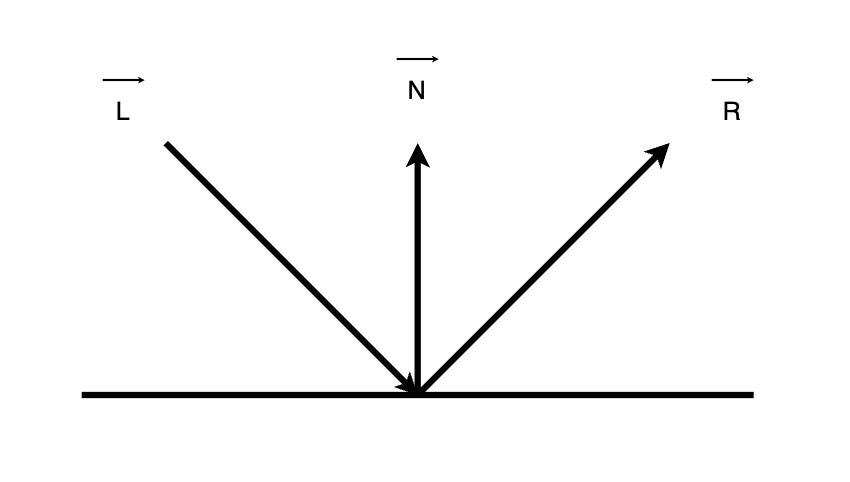
평면과 노말벡터 N, 빛의 방향 L, 반사된 빛의 방향 R이 있을 때 우리가 알 수 있는 값은 N과 L일 것이다.
그럼 우리가 R을 구하면 반사된 빛의 방향을 알 수 있는데 알 수 있는 방법은 다음과 같다.
우선 다음과 같이 L의 방향을 바꾸고 -L과 N을 내적하면 cos값을 알 수 있는데 원래 빛의 방향이었던 L에 cos을 두 번 더하면 우리가 원하는 R을 알 수 있을 것이다.

그럼 우리는 이제 L, N, R의 값을 모두 알았고 그 다음은 이제 카메라와 연관이 있다.

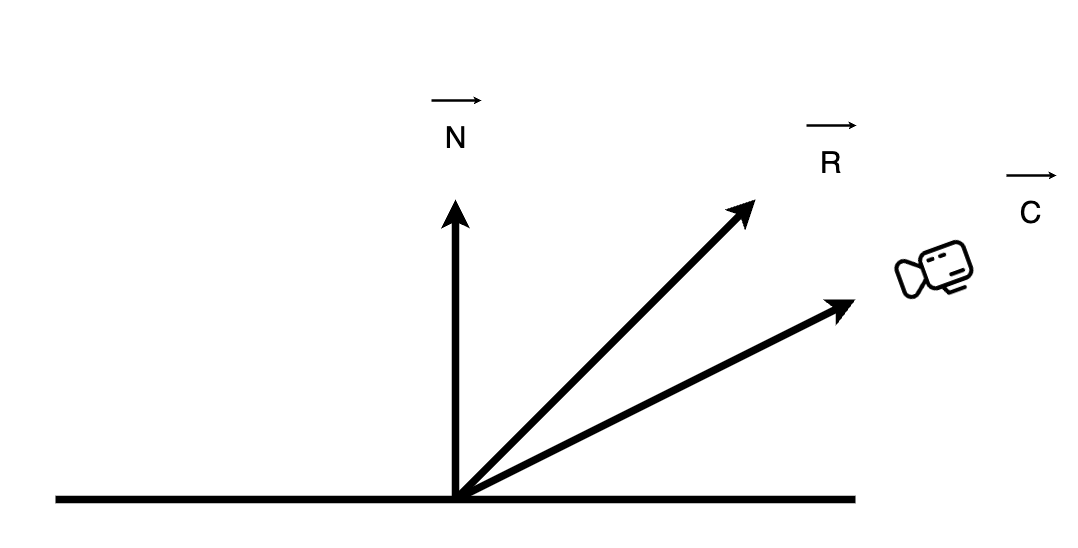
다음과 같이 중심점에서 카메라까지의 벡터 C를 추가했을 때 R과 C사이의 cos값을 계산해서 우리가 빛의 세기를 조정할 수 있을 것이다.
만약 C가 R과 동일하여 cos이 0이라면 빛이 정확히 반사되어 카메라에 꽃힌 것이고, 만약 R과 각도가 많이 벌어져있다면 cos값이 커질 것이다.

계산은 중심점 pos와 카메라의 위치에 따른 벡터를 normalize해서 단위벡터로 만들면 C가 나올 것이고, R과 C를 내적하면 cos값이 나올 것이다. 우리는 이 cos값을 해당 Material의 Specular값에 곱해서 최종 값을 내면 될 것이다.