프로그래머스 - 카카오 2020 / 자물쇠와 열쇠

자물쇠와 열쇠 (2021. 07. 20) Lock

문제 및 풀이 주소

Programmers
Git Solution

문제 설명

고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.
잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.
자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.
열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.

제한사항

• key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
• lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
• M은 항상 N 이하입니다.
• key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
• 0은 홈 부분, 1은 돌기 부분을 나타냅니다.

key	lock	result
[[0, 0, 0], [1, 0, 0], [0, 1, 1]]	[[1, 1, 1], [1, 1, 0], [1, 0, 1]]	true

문제 해결

해결 방안 추측

문제를 보고 이해할때, 탐색에 관련된 문제인것은 느낄 수 있었으나, '어라? 결국 맞는지 틀린지 true/false만 체크하면 되니까 패턴값으로 비교하면 더 편하지 않을까? 했었다. 하지만 미친듯한 예외 상황과 테스트케이스의 실패, 결과값을 체크할때 true/false니까 명확하게 잘못된 테스트 케이스를 알수가 없었다. 구현 방식을 일반방식과 다르게 하려고도 하니 구글링의 도움을 받을 수 조차 없었다. 처음에 문제를 포기하려고 했으나, 스터디 모임의 잡부(감사합니다)님에게 가능할 것 같다는 의견을 듣고나서, 현재 문제를 해결하였다.

이슈 케이스

배열을 인덱스화 하여 매칭을 하려고 했으나, 해당 사항을 체크하지 못하였다.

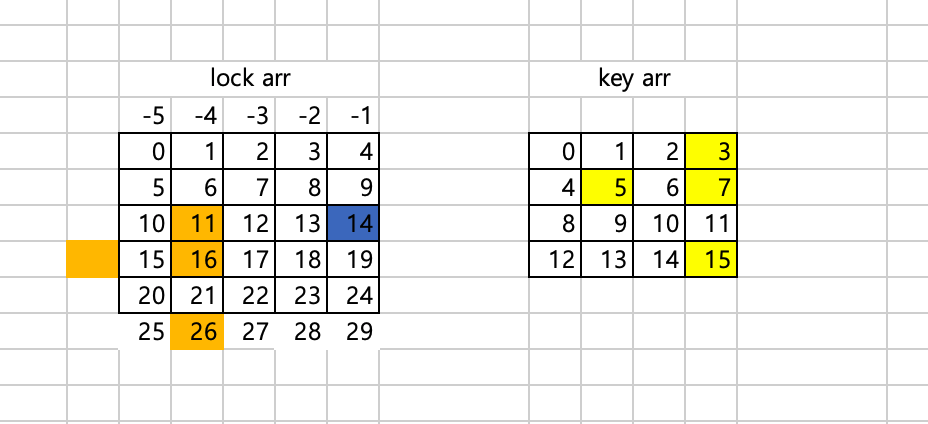
그림을 보면 lock과 key의 패턴이 그림과 같을 때, 11 인덱스를 기준으로 패턴을 만들 때, 계산 공식에 의해서 14 인덱스의 위치값이 변하게 된다.. 공식 자체에는 문제가 없었으나(알고보니 공식도 틀렸었다) 이런 케이스 에서 원하는 패턴값이 만들어 지지 않는 다는것을 깨달았다.

문제 해결

lock 배열의 크기를 가상 배열로 만들어서 이슈케이스처럼 값이 넘어가는 경우가 없도록 하자!

애초에 값이 넘어갈 수 없는 상황을 만들면 될 것 같았다.(나중에 답보니까 확장해서 한 사람들이 많았다)
그렇다면 어느 정도 크기까지 확장해야 할까? 하다가 다음과 같이 기준을 정하였다.

• key 배열의 최대 크기는 lock 배열의 크기니까 key 배열과 lock 배열이 같을 경우가 가장 큰 값이다.
• lock배열의 끝 자리 인덱스에서 패턴을 찾아야 할 경우가 있으므로 최대값은 3배로 한다.
• 3배인 경우에는 항상 lock 배열의 실제 값은 가운데에 위치해야 한다. ( 그래야 상하좌우 다 커버 가능)

다음과 같은 조건이 되면 해당 그림처럼 나오게 된다.

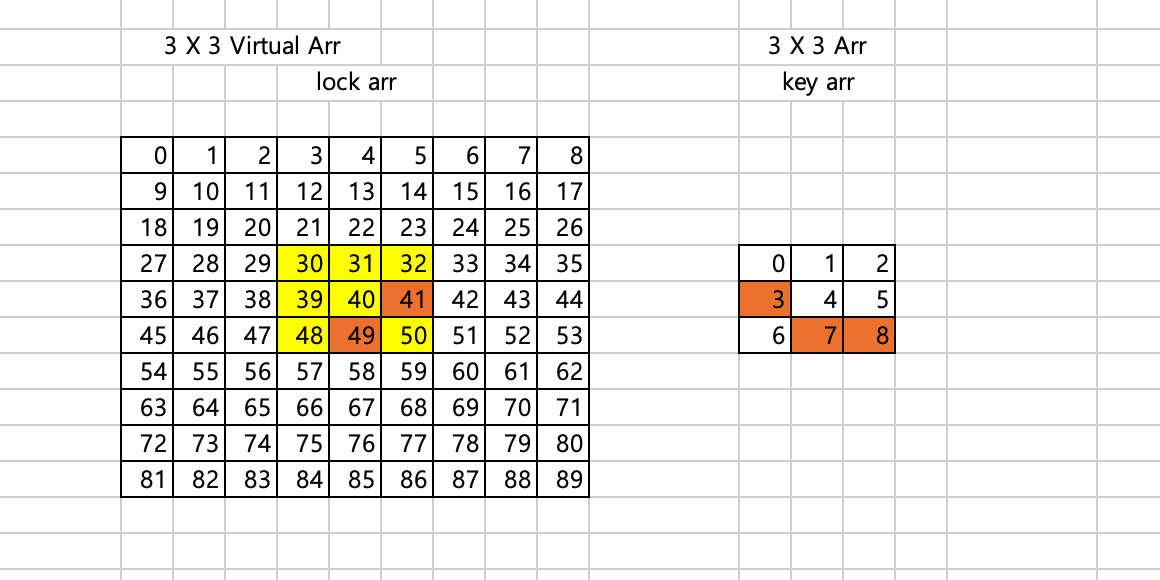
끝자리에 매칭해야할 번호가 있어도, 절대로 패턴의 모양이 변하지 않는다.(가상 범위값을 N*3 -1 로 해도 될듯하다, 겹쳐지는 라인은 반드시 필요하니까)

해당 인덱스를 만드는 코드는 다음과 같다.

/*
        virtualArr               virtualRealLockList
        1 1 1 1 1 1 1 1 1 
        1 1 1 1 1 1 1 1 1 
        1 1 1 1 1 1 1 1 1 
        1 1 1 1 1 1 1 1 1              30 31 32
        1 1 1 1 1 0 1 1 1              39 40 41
        1 1 1 1 0 1 1 1 1              48 49 50
        1 1 1 1 1 1 1 1 1 
        1 1 1 1 1 1 1 1 1 
        1 1 1 1 1 1 1 1 1
*/
public void setVirtualLock(int[][] lock){
    // 자물쇠의 크기를 확장하는데 자물쇠의 크기와 키의 크기가 같을 경우, 앞뒤로 키의 배열이 올 수 있으므로 총 3배
    // 실제 크기
    int length = lock.length;
    // 관련 변수 초기화
    virtualArr = new int[length*3][length*3];
    virtualRealLockList = new ArrayList<>();

    // 가상 배열 적용 loop
    int count = 0;
    for(int i = 0; i < virtualArr.length; i++){
        for(int j = 0; j < virtualArr.length; j++){
            // 가상 배열 범위중, 실제 lock 배열의 값을 가운데에다가 설정
            // 조건은 (0,0) ~ (length-1, length-1)이 만들어지는 실제 범위 이므로 (length, length) ~ (length * 2 -1, length * 2 -1)로 변환한다.
            if(i >= length && j >= length && i <= (length * 2) -1 && j <= (length * 2) -1){
                virtualArr[i][j] = lock[i-length][j-length];
                virtualRealLockList.add(count);
            }else{
                virtualArr[i][j] = 1;
            }
            count++;
        }
    }
}

공식 만들기 - 로테이션

배열의 값을 회전하기 위해서 다음과 같은 공식을 만들어 적용하였다.

N * (N - 행번호) - (N - 열번호)
int locationValue = size * (size - row) - (size - column);

먼저 2차원 배열을 1차원 배열로 flat하게 펼쳐놓은 다음, loop를 돌면서 locationValue 변수의 값을 flat배열에서 찾아서 새로이 [0][0]부터 채운다.

코드는 다음과 같다.

public int[][] rotation(int[][] arr){
    // 2차원 배열을 1차원 배열로 변환한다.
    int[] flatArr = Arrays.stream(arr).flatMapToInt(Arrays::stream).toArray();

    // loop 관련 변수
    int size = arr.length;
    int column = 0;
    int row = 0;

    // 임시 1차원 배열
    int[] tempArr = new int[size * size];
    for(int idx = 0; idx < flatArr.length; idx++){
        // 로테이션 위치값 - 공식에 의한 인덱스값을 찾는다.
        //N * (N - 0) - (N - 1)|N * (N - 1) - (N - 1)|N * (N - 2) - (N - 1)
        //N * (N - 0) - (N - 2)|N * (N - 1) - (N - 2)|N * (N - 2) - (N - 2)
        //N * (N - 0) - (N - 3)|N * (N - 1) - (N - 3)|N * (N - 2) - (N - 3)
        int locationValue = size * (size - row) - (size - column);
        // 인덱스값을 1차원으로 펼친 flatArr에서 값을 임시 1차원 배열에 할당한다.
        tempArr[idx] = flatArr[locationValue];
        if( row == (size - 1)){
            row = 0;
            column++;
        }else{
            row++;
        }
    }

    // 1차원 temp 배열을 2차원 result 배열로 변환
    int[][] result = new int[size][size];
    row = 0;
    column = 0;
    for (int value : tempArr) {
        result[column][row] = value;
        if ((size - 1) == row) {
            row = 0;
            column++;
        } else {
            row++;
        }
    }
    return result;
}

공식만들기 - 패턴값 찾기

패턴을 찾기 위해 다음과 같은 공식을 적용하였다.

(lock기준점 - key기준점) + key value + (lock size - key size) * ((key value / key size) - key기준열)
굉장히 복잡하여 코드에서는 변수로 나누어서 적용하였다. 솔직히 나도 내가 이런 공식을 만들어 낼줄은 몰랐다.. 굉장히 오랜시간 엑셀을 끄적이면서 테스트 하고 좌절하였다. 물론 실제 코딩테스트를 본다면 나는 바로 떨어지겠지

코드는 다음과 같다(어려우므로 각 변수에 주석을 상세히 적었다.)
목표하는 바는 다음과 같다.

• key와 lock의 배열값이 달라져도 패턴의 모양은 변하면 안된다.
• 인덱스의 번호값이 완전히 일치해야 하므로 lock배열의 위치중 하나가 key배열의 위치중 하나와 일치시킨다음 만들어진 패턴값을 비교한다.
• 필터링을 거쳐 lock패턴과 key패턴이 사이즈도 같고 저장된 데이터가 같으면 true를 반환한다.

/*
    lock의 41번 인덱스가 key의 3인것으로 가정하고 패턴을 만들었을 경우
    standardPoint  38 | 38 | 38
    basePoint      41 | 45 | 46
    plusPoint       0 |  6 |  6
    newPoint       41 | 51 | 52
*/
// 변환된 lock 배열의 특정 위치에서 key의 패턴을 만드는 메소드
private List<Integer> findPattern(List<Integer> keyList, int standardLockNo, int idx){
    List<Integer> resultList = new ArrayList<>();
    // lock 패턴의 기준점 계산, key 패턴이 loop하면서 해당 값이 loop 패턴의 값이 되도록 하기 위해
    int standardPoint = standardLockNo - keyList.get(idx);
    // key 패턴의 값이 key 배열의 몇번째 row에 있는지 계산하기 위해
    int standardRow = keyList.get(idx) / keyLength;
    // key 패턴 loop
    for(int keyNo : keyList){
        // 기본값, 각 기준에 해당하는 key 패턴은 해당 lock 패턴의 값과 일치하게 나와야 한다.
        int basePoint = keyNo + standardPoint;
        // lockLength - keyLength -> 배열 크기가 다른 lock과 key배열의 차이
        // (keyNo / keyLength) - standardRow -> key 패턴의 값이 실제 어느 열에 존재하는지
        // lock 패턴과 key 패턴의 크기가 다를때, 같은 패턴의 모양을 만들어주기 위해 크기가 차이나는 만큼 인덱스 값을 더해서 만든다.
        int plusPoint = (lockLength - keyLength) * ((keyNo / keyLength) - standardRow);
        // basePoint와 plusPoint의 합으로 최종적인 virtual lock pattern의 위치 값을 찾는다.
        int newPoint = basePoint + plusPoint;

        // 필터링 - 확장되었지만 실제로는 확정 전의 lock 패턴에 값이 존재하는 key의 값만이 대상이 되므로
        // 해당 범위가 아닌 point값은 lock의 실제범위를 벗어나는 값이다.
        if(virtualRealLockList.contains(newPoint)){
            resultList.add(newPoint);
        }
    }
    return resultList;
}

// 최종적으로 필터링 이후 만들어진 두 패턴을 비교하는 메소드
private boolean diffList(List<Integer> keyList, List<Integer> lockList){
    // 실제 범위이외의 데이터는 필터링 처리 되었기 때문에 두 리스트의 사이즈는 같으며 포함되어야 한다.
    // 단순 contains 사용시, 패턴에서 자물쇠와 키가 둘다 1인 케이스가 있어서 테스트 케이스 3개가 실패한다.
    // 참고) 실제 정답에서는 XOR처리라고 되어있다.
    if(keyList.size() == lockList.size()){
        return lockList.containsAll(keyList);
    }
    return false;
}

테스트 결과

테스트 번호	통과여부	메모리 및 시간	테스트 번호	통과여부	메모리 및 시간
테스트 1	통과	(3.27ms, 52.7MB)	테스트 20	통과	(116.46ms, 58.8MB)
테스트 2	통과	(0.11ms, 52.1MB)	테스트 21	통과	(8.61ms, 54.3MB)
테스트 3	통과	(24.22ms, 54.9MB)	테스트 22	통과	(90.99ms, 67.5MB)
테스트 4	통과	(0.11ms, 54MB)	테스트 23	통과	(8.79ms, 52.8MB)
테스트 5	통과	(42.27ms, 56.9MB)	테스트 24	통과	(15.76ms, 52.5MB)
테스트 6	통과	(23.67ms, 52.5MB)	테스트 25	통과	(56.86ms, 56.6MB)
테스트 7	통과	(2.50ms, 52.2MB)	테스트 26	통과	(279.80ms, 71.3MB)
테스트 8	통과	(68.75ms, 56.8MB)	테스트 27	통과	(1932.11ms, 200MB)
테스트 9	통과	(184.03ms, 71.7MB)	테스트 28	통과	(28.92ms, 55.1MB)
테스트 10	통과	(758.60ms, 75.6MB)	테스트 29	통과	(10.13ms, 52.7MB)
테스트 11	통과	(1442.06ms, 141MB)	테스트 30	통과	(60.21ms, 58.6MB)
테스트 12	통과	(0.08ms, 52.6MB)	테스트 31	통과	(80.87ms, 60.1MB)
테스트 13	통과	(42.50ms, 56MB)	테스트 32	통과	(481.54ms, 76.5MB)
테스트 14	통과	(6.44ms, 51.7MB)	테스트 33	통과	(108.59ms, 70.8MB)
테스트 15	통과	(0.66ms, 51.9MB)	테스트 34	통과	(0.49ms, 52.4MB)
테스트 16	통과	(44.66ms, 56.5MB)	테스트 35	통과	(10.97ms, 52.6MB)
테스트 17	통과	(14.17ms, 52.7MB)	테스트 36	통과	(17.22ms, 53MB)
테스트 18	통과	(24.64ms, 52.8MB)	테스트 37	통과	(13.21ms, 52.6MB)
테스트 19	통과	(4.12ms, 52.6MB)	테스트 38	통과	(10.40ms, 52.8MB)

정통 풀이 방식

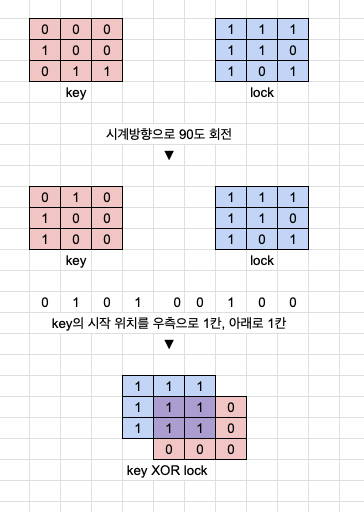
lock의 배열과 key의 배열을 겹치게 만들어 lock배열의 모든 원소가 1인지를 체크만 하면 된다. 겹치는 부분은 그림과 같이 2X2를 잡지는 않고 겹치는 부분이 1X1로 왼쪽 위부터 1X1, 2X2.. 로 하나의 배열이 남은 하나의 배열을 탐색하면서 체크하면된다. 실제 풀이 방식을 보니 나의 방식이 얼마나 어려운 방식인지 세삼 알게되었다. (나는 공식을 만들었는데...)
또한 해당 방법에서는 lock과 key배열의 크기 차이를 알 필요가 없다. 그냥 탐색만 하면 되니까, 그리고 중요한게 lock배열과 key배열의 값이 둘다 1인경우인데 이럴때는 열쇠가 자물쇠를 통과할 수 없는 케이스가 되므로 0으로 치환하던지 return false를 해주면 된다.

후기

오랫동안 시간을 들였고, 많은 실패로 좌절했다. 다음부터는 문제를 보고 어떤식으로 푸는지 확인을 하고 구현을 해야겠다는 생각을 하였다. 예제로 주어지는 문제에서는 테스트케이스를 모두 체크할 수가 없으므로 실제 제대로 구현했다고 해도 테스트케이스의 실패가 너무 많았다. 지금은 공부용이라 오랜시간을 들여 풀긴 했지만, 실제로는 정해진 시간에 문제를 풀어야 하기 때문에 해당 방식처럼 혼자 다른방향으로 가는것은 하지 말야겠다.