Elasticsearch 형태소분석의 최장일치법

최장일치법 (Longest Matching)이란?

최장일치법은 한 어절 내에서 분절이 가능한 여러 형태소 중에서 가장 긴 형태소를 선택하는 방법. 이 방법은 일반적으로 한국어 형태소 분석에서 사용되며, 주어진 문장을 형태소 단위로 분리할 때 가장 일반적인 방식 중 하나.
최장일치법은 주어진 텍스트에서 연속된 글자들을 형태소로 간주하고, 사전에 등록된 어휘 정보와 비교하여 어휘를 찾아낸다.

최장일치법, 최단일치법 예제

문장: "감기는"

최장일치법 (Longest Matching):

[감기],[는]

최단일치법 (Shortest Matching):

[감],[기],[는]

논문예시

[논문보기 - 한국어 형태소 처리와 사전 ](DBPIA-NURIMEDIA (snu.ac.kr))

형태소분석트리를 정의하고, 이 정의에 따른 형태소분석트리의 탐색에 있어서 최단일치법과 최장일치법을 정의한다. 그리고 탐색방법에 따른 최단일치법과 최장일치법의 차이점을 비교한다.
어떤 어절이 주어졌을 때, 이 어절에 대한 형태소분석트리는 사전에 들어 있는 형태소에 의해서 결정된다. 따라서, 형태소분석트리를 정의하기 전에 다음과 같은 변수가 주어졌다고 가정하자.

• 모든 가능한 형태소로 구성된 사전(dictionary)을 $D$라 하자.
• 어떤 어절 $E$는 $E$=$E_{1}$ $\cdots$ $E_{n}$이라 하자. 여기서 $E_{i}(i \leq n)$는 하나의 자소이다.
• $M_{i, j}(i \leq j)$는 $E_{i} \cdots E_{j}$로 구성된 사전 $D$에 있는 형태소라 하자.
• $M^{\prime}{ }_{i, n}(i \leq n)$는 $E_{i} \cdots E_{n}$로 구성된 사전에 없는 $E$의 suffix라 하자.

[정의 1] 형태소분석트리 (MAT: Morphological Analysis Tree)}

형태소분석트리는 다음과 같은 조건을 만족하는 하나 이상의 노드로 구성된 순서화된 트리(ordered tree)이다.

• 루트(root)라 불리우는 특별히 지정된 노드(node) $M_{0,0}$가 있다
• 한 노드 $M_{i, j}$의 자식 노드(child node)는 $M_{j+1, k}(k \leq n)$로 사전 $D$에 있는 모든 가능한 노드이다.
• 한 노드의 자식 노드 중 가장 오른쪽 노드 $M_{i, j}$가 $j \neq n$이면 새로운 $M^{\prime}{ }_{j+1, n}$을 이 노드의 가장 오른쪽 노드로 둔다.

[정의 2] 최단일치법 (Shortest Match Stratege)

두 노드 간의 접속성을 검사하면서 MAT를 Depth-first Search 방법으로 루트 노드로부터 단말 (terminal) 노드까지의 모든 노드들이 접속 가능한 경로(path) 하나를 찾는 방법 이 다.

[정의 3] 최장일치법 (Longest Match Strategy)

두 노드 간의 접속성 을 검사하면서 MAT를 Breadth.first Search 방법으로 루트 노드로부터 단말 노드까지의 모든 노드들이 접속 가능한 경로 하나를 찾는 방법이다.

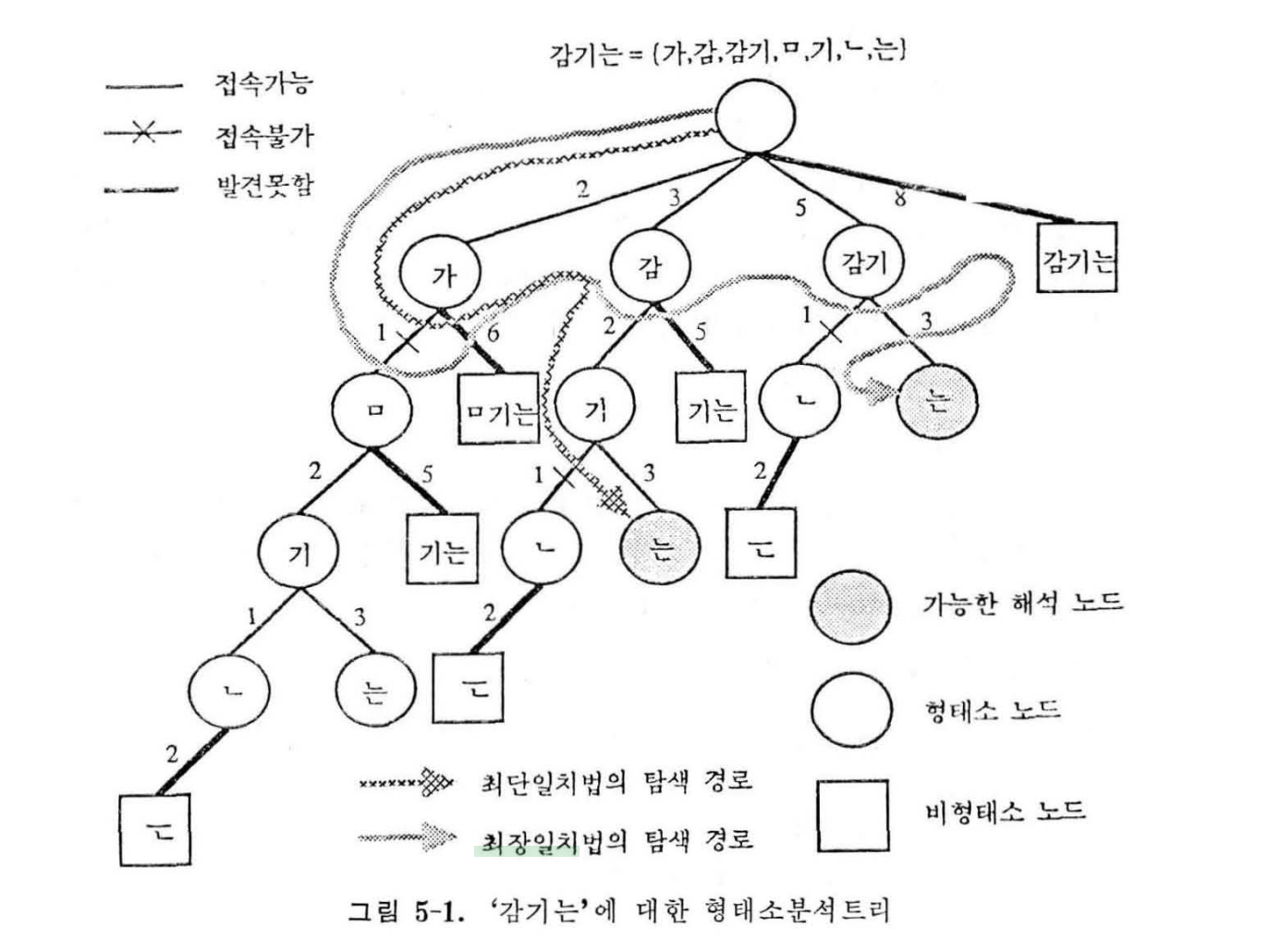
이 정의에 의해서 어절 감기는에 대한 MAT를 그리면 그립 5-1과 같다.
여기에서 감기는에서 가능한(사전 $D$에 있는) 어절은 다음과 같이 정의한다고 한다.

[가], [감], [감기], [ㅁ], [기], [ㄴ], [는]

그림에서 원은 $M_{i,j}$인 비형태소 노드를 표시한다. 빗금친 원은 이 어절의 가능한 해석 중의 하나를 나타낸다. 이 노드를 가능한 해석 노드라 부른다.

최단일치법과 최장일치법 를 비교할 수 있는 척도 (criteria) 로는 접속가능성 검사 수와 패턴 비교 를 들 수 있다.

• 접속가능성 검사 회수는 MAT를 여행한 경로의 합이다.
• 패턴 비교 횟수는 여행(traverse)한 경로의 길이의 합이다. 두 개의 노드 $M_{i,j}$ 와 $M_{j,k}$(또는 $M^{\prime}{ }_{j, k}$) 사이의 경로의 길이는 $k-j+1$ 이다.

그림에서 최단일치법의 경우, 접속 가능한 검사의 횟수는 7회이고, 패턴 비교 수는 2+1+6+3+2+1+3=18회 이다. 최장일치법의 경우, 접속가능성 검사 수는 6회이고, 패턴 비교 수는 2+3+5+7+1+3=21회이다.
최단일치법은 Depth-first Search를 하고 최창일치법 은 Breadth-first Search를 하므로, 최단일치법은 가능한 해석 노드가 왼쪽 가지에 치우친 경우에,최장일치법은 요른쪽에 치우친 경우에 유리하다.

MAT는 오른쪽으로 치우칠수록 깊이가 낮아지고 경로의 길이 (path length)가 커지는 특성을 가지고 있다.
최장일치법은 자식 노드를 전부 검사해야 하므로 패턴 비교 횟수가 더 크다. 반면에 최단일치법은 접속 가능성 검사의 횟수가 커질 수 있다.
형태소 노드로 끝나는 단말 노드는 어절이 경로 상에 있는 형태소들로 분절될 수 있읍을 의미한다. 이들 중 접속 가능성 검사를 하여 루트 노드로부터 단말 노드까지 접속 가능한 경 로의 수(즉, 가능한 해석 노드의 수)는 이 어절의 애매성의 수이다.
애매성이 발생했을 경우, 최단일치법은 최초 적합(first-fit)을 찾으려는 방법이고, 최장일치법은 이러한 경우 더 긴 형태소가 맞을 가능성이 높다는 한국어의 특성을 이용하여 최적 적합(best-fit)을 찾으려는 방법으로 볼 수 있다.

최장분리법 사용 이유

대부분의 한국어 형태소 분석 작업에서는 최장일치법이 더 효과적이며 신뢰성 있게 사용. 최장일치법은 형태소의 길이를 우선시하고, 의미 단위를 보존하며, 문장 구조를 유지하는 데 도움을 주므로 자연어 처리에서 더 널리 사용.

최장분리법 장점

• 의미 단위 보존: 최장일치법은 주어진 텍스트에서 가장 긴 형태소를 선택하므로 단어나 어구의 의미 단위를 보존하는 데 도움. 이는 문장의 구조를 더 잘 보존하고 의미 해석을 더 쉽게 만든다.

• 문장 구조 유지: 최장일치법은 주어진 문장을 단어나 어구 단위로 나누는 데 더 적합하며, 이로 인해 문장의 구조가 유지. 이는 문장 분석 및 해석에 도움이 되며, 자연어 처리 작업에서 유용.

• 분석의 일관성: 최장일치법을 사용하면 주어진 텍스트를 분석하는 과정이 일관성을 가지게 된다. 모든 형태소를 가장 긴 형태소로 나누므로 형태소 분석 결과가 일관적이고 예측 가능.

• 언어 모델과의 결합: 최장일치법은 많은 한국어 언어 모델과 자연어 처리 도구와 잘 결합. 대부분의 언어 모델과 자연어 처리 도구는 최장일치법을 기반으로 개발되어 있으며, 따라서 최장일치법을 사용하면 이러한 도구와 모델을 더 효과적으로 활용.

최단분리법 단점

• 의미 분리 문제: 최단일치법은 주어진 텍스트에서 가장 짧은 형태소를 선택하므로 단어나 구문의 의미가 분리될 수 있음. 이로 인해 문장의 구조가 올바르게 분석되지 않을 수 있으며, 의미 해석이 어려워짐.
  
• 불일치 문제: 최단일치법을 사용하면 어절이 의미 단위로 분리되지 않을 수 있으며, 이는 자연어 처리 작업에서 문제를 일으킬 수 있음. 예를 들어, "좋아하지"와 "않아요"를 분석할 때, 최단일치법을 사용하면 "좋아하지"가 "좋아"와 "하지"로 분리될 수 있으며, 의미가 불일치.
  
• 일관성 부족: 최단일치법을 사용하면 동일한 텍스트에 대해 다양한 형태소 분석 결과가 나올 수 있으며, 이로 인해 결과의 일관성이 부족할 수 있음. 이는 자연어 처리 알고리즘과 모델의 예측과 일치하지 않을 수 있음.
  
• 구문 분석 어려움: 최단일치법은 문장의 구문 분석을 어렵게 만들 수 있으며, 문장의 구조를 파악하는 데 어려움을 초래.