펭귄들의 종, 서식 지역, 부리 길이와 부리 깊이, 날개 사이즈, 성별, 그리고 몸무게 데이터 셋이 있다.
독립 변수를 선택하고, 몸무게를 예측하는 선형 회귀 모델을 torch를 이용해서 만들고 학습시킬 것이다.
import pandas as pd
df = pd.read_csv("./data/penguins.csv")판다스를 이용하여 데이터 프레임을 만든다.
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
def load_penguin_dataset():
df = pd.read_csv("./data/penguins.csv")
df = df.dropna(subset="body_mass_g")
sex_mapping = {'MALE': 1, 'FEMALE': 0}
df['sex'] = df['sex'].map(sex_mapping)
df['sex'] = df['sex'].fillna(-1)
spec_mapping = {'Gentoo': 2, 'Adelie': 1, 'Chinstrap': 0}
df['species'] = df['species'].map(spec_mapping)
df['species'] = df['species'].fillna(-1)
X = df.drop(["body_mass_g"], axis=1)
y = df["body_mass_g"]
return train_test_split(X, y, train_size=0.8, random_state=1234)
x_train, x_test, y_train, y_test = load_penguin_dataset()load_penguin_dataset 함수를 선언한다.
penguins.csv 데이터를 불러와 처리하고, 학습용 데이터와 테스트용 데이터로 분할하여 반환한다.
df = pd.read_csv("./data/penguins.csv"): CSV 파일을 불러와 DataFrame 객체에 저장한다.
df = df.dropna(subset="body_mass_g"): 'body_mass_g' 열에 NaN(누락된 값)이 있는 행을 제거한다.
다음 네 줄은 'sex' 열의 값을 숫자로 매핑하고, 누락된 값을 -1로 채운다.
이어서 두 줄은 'species' 열의 값을 숫자로 매핑하고, 누락된 값을 -1로 채운다.
X = df.drop(["body_mass_g"], axis=1): 'body_mass_g' 열을 제외한 나머지 열을 X 변수에 저장한다.
y = df["body_mass_g"]: 'body_mass_g' 열만 y 변수에 저장한다.
return train_test_split(...): X와 y를 학습용 데이터와 테스트용 데이터로 분할하고, 이를 반환한다.
마지막 줄에서는 load_penguin_dataset() 함수를 호출하여 데이터를 분할하고, 이를 x_train, x_test, y_train, y_test 변수에 저장한다.
import seaborn as sns
from matplotlib import pyplot as plt
x_train["body_mass_g"] = y_train
cmap = sns.diverging_palette(240, 10, n=9, as_cmap=True)
plt.figure(figsize=(10, 8))
sns.heatmap(
x_train.corr(),
annot=True,
fmt=".2f",
cmap=cmap,
linewidths=.5,
annot_kws={"size": 7}
)seaborn과 matplotlib 라이브러리를 이용해 펭귄 데이터셋의 상관관계를 시각화한다.
독립변수와 관련있는 종속변수를 골라내기 위한 작업이다.
예를 들어 잘생긴 남자 예측하는데, 코와 눈 크기는 몰라도 엄지손가락 굵기, 똥꼬 넓이 이런거는 상관 없잖아?ㅋㅋ
x_train["body_mass_g"] = y_train : y_train의 값을 x_train의 새로운 열 'body_mass_g'에 할당한다.
cmap = sns.diverging_palette(240, 10, n=9, as_cmap=True) : 색상 맵을 생성하는 코드다. sns.diverging_palette() 함수는 두 개의 색상 사이의 발산하는 팔레트를 생성한다. 여기서는 색상의 시작점이 240(파란색)이고, 종료점이 10(빨간색)이다. n=9는 색상 단계의 수를 나타내며, as_cmap=True는 결과를 colormap으로 반환한다.
plt.figure(figsize=(10, 8)) : 그림(figure)의 크기를 10x8 인치로 설정한다.
sns.heatmap(...) : 상관계수 히트맵을 생성한다.
x_train.corr(): 데이터의 상관계수를 계산한다.
annot=True: 각 셀에 상관계수의 값을 표시한다.
fmt=".2f": 상관계수의 값을 소수점 둘째 자리까지 표시한다.
cmap=cmap: 위에서 정의한 colormap을 사용한다.
linewidths=.5: 각 셀 사이의 선의 두께를 설정한다.
annot_kws={"size": 7}: 표시되는 숫자의 크기를 7로 설정한다.
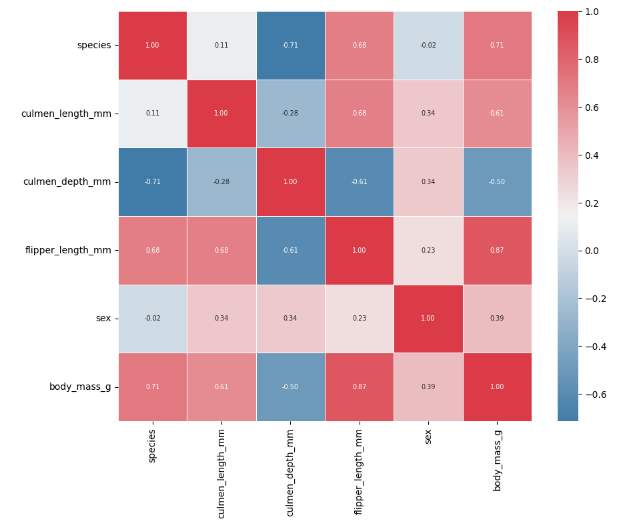
"flipper_length_mm"가 적절해 보인다.
minmax_scaler = MinMaxScaler()
df = df[["flipper_length_mm", "body_mass_g"]]
df[["flipper_length_mm", "body_mass_g"]] = minmax_scaler.fit_transform(df)"flipper_length_mm"와 "body_mass_g"을 Min-Max 스케일링으로 정규화하는 작업을 수행한다.
df.isna().sum()
df = df.dropna()결측값을 확인하고 제거해준다.
def loss_function(w):
return ((df["flipper_length_mm"] * w - df["body_mass_g"]) ** 2).sum() / len(df)
losses = []
w_candidates = np.arange(0, 2.1, 0.05)
for w_candidate in w_candidates:
losses.append(loss_function(w_candidate))
plt.scatter(w_candidates, losses, s=5, color="red")
_ = plt.xticks(np.arange(0, 2.1, 0.2))
plt.xlabel("W")
plt.ylabel("loss")
def plot_line(w, bias, color):
x = np.linspace(0, 1, 100)
y = w * x + bias
plt.plot(x, y, color=color, label=f"w={w}")가중치 w 값에 따라 손실 함수의 값을 계산하고, 그 결과를 시각화해본다.
loss_function(w): 이 함수는 가중치 w를 입력으로 받아, 선형 관계 y=wx의 예측값과 실제 body_mass_g 값의 차이를 계산하여 그 차이의 제곱의 평균을 반환한다.
w_candidates = np.arange(0, 2.1, 0.05): 가중치 w의 후보 값들을 0부터 2.1까지 0.05 간격으로 생성한다.
for w_candidate in w_candidates: 각 w 후보에 대해 손실 함수의 값을 계산하고 그 결과를 losses 리스트에 추가한다.
plt.scatter(w_candidates, losses, s=5, color="red"): 각 w 후보에 대한 손실 함수의 값을 산점도로 시각화한다.
plt.xlabel("W")와 plt.ylabel("loss"): x축과 y축의 레이블을 설정한다.
plot_line(w, bias, color) 함수: 주어진 w 값과 편향에 대해 선을 그리는 함수다. 여기서는 입력 데이터가 [0, 1] 범위로 정규화되었기 때문에 x값의 범위도 [0, 1]로 설정되어 있다.
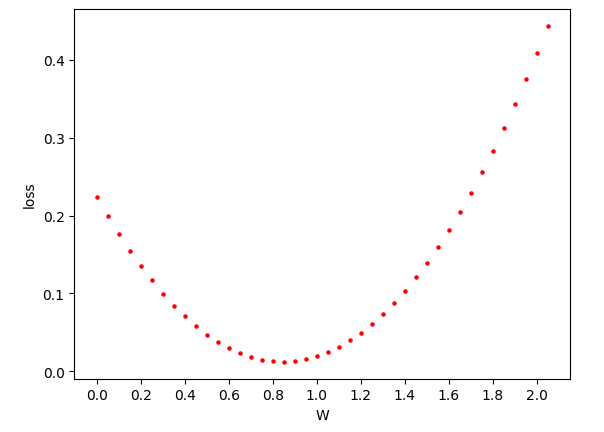
0.85 근처가 최소값으로 판단되니, 그 값으로 그래프를 그려보자.
plt.scatter(df["flipper_length_mm"], df["body_mass_g"], s=1)
plot_line(0.85, 0, "red")
plt.legend()
plt.ylim(0, 1)
plt.xlabel("scaled carat")
plt.ylabel("scaled price") 스케일링된 펭귄 데이터의 "flipper_length_mm"와 "body_mass_g" 사이의 관계를 시각화하고, 그 관계를 나타내는 예상 선을 그래프에 추가한다.
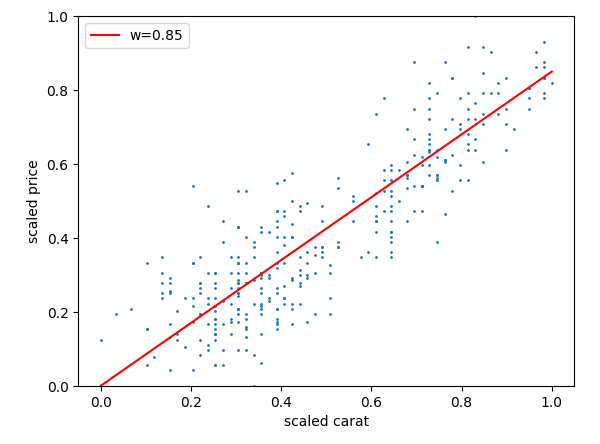
이제 모델을 만들어보자.
import torch
class LinearRegression(torch.nn.Module):
def __init__(self, input_dim, output_dim):
super(LinearRegression, self).__init__()
self.linear = torch.nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
model = LinearRegression(input_dim=1, output_dim=1)
learning_rate = 0.3
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = torch.nn.MSELoss()
epochs = 100
inputs = torch.Tensor(df[["flipper_length_mm"]].values)
labels = torch.Tensor(df[["body_mass_g"]].values)
losses = []
lines = []
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
# 현재 모델을 이용해서 예측값 계산
outputs = model(inputs)
# 오차 계산
loss = criterion(outputs, labels)
# 편미분 수행
loss.backward()
# learning rate만큼 모델 파라미터 업데이트
optimizer.step()
losses.append(loss.item())
weight = model.linear.weight[0].item()
bias = model.linear.bias[0].item()
if (epoch + 1) % 10 == 0:
lines.append((weight, bias))
print('epoch {}, loss {}'.format(epoch+1, loss.item()))model = LinearRegression(input_dim=1, output_dim=1): 입력 차원과 출력 차원이 모두 1인 LinearRegression 모델의 인스턴스를 생성한다.
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate): 경사 하강법을 사용하여 최적화를 수행한다. learning_rate는 학습률이다.
criterion = torch.nn.MSELoss(): 오차(손실)를 계산하기 위한 평균 제곱 오차 함수를 설정한다.
inputs = torch.Tensor(df[["flipper_length_mm"]].values)와 labels = torch.Tensor(df[["body_mass_g"]].values): 데이터프레임에서 필요한 열의 값을 추출하여 PyTorch 텐서로 변환한다.
for epoch in range(epochs): 주어진 에포크 수만큼 반복하여 모델을 학습한다. 모델의 출력은 입력을 사용하여 계산된다.
loss = criterion를 사용하여 예측값과 실제 라벨 사이의 손실을 계산한다.
loss.backward()는 편미분을 수행하여 그래디언트를 계산한다.
optimizer.step()을 사용하여 모델의 파라미터를 업데이트한다.
losses.append(loss.item()): 현재 에포크의 손실 값을 losses 리스트에 추가한다.
weight = model.linear.weight[0].item()와 bias = model.linear.bias[0].item(): 학습된 모델의 가중치와 편향을 추출한다.
if (epoch + 1) % 10 == 0: 에포크가 10의 배수일 때마다 가중치와 편향의 값을 lines 리스트에 추가하고, 손실 값을 출력한다.
아래와 같이 출력된다.
epoch 10, loss 0.0605011060833931
epoch 20, loss 0.041538361459970474
epoch 30, loss 0.029397374019026756
epoch 40, loss 0.021624045446515083
epoch 50, loss 0.016647135838866234
epoch 60, loss 0.013460645452141762
epoch 70, loss 0.0114204790443182
epoch 80, loss 0.01011425070464611
epoch 90, loss 0.009277934208512306
epoch 100, loss 0.008742478676140308시각화를 해보자.
plt.plot(losses, label="train")
plt.xlabel("epochs")
plt.ylabel("loss")
plt.legend()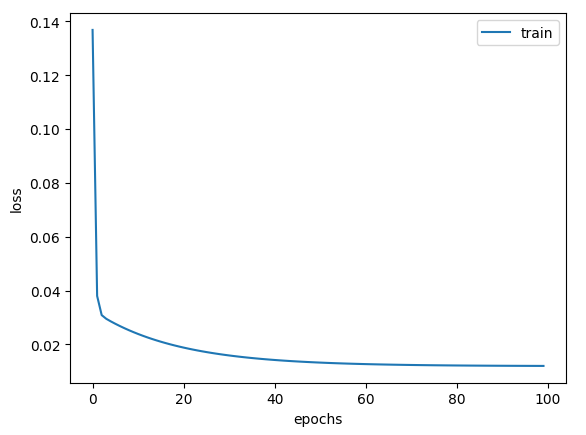
figure = plt.figure(figsize=(12, 12))
axs = []
for i in range(9):
ax = figure.add_subplot(3, 3, i+1)
w, bias = lines[i]
x = np.linspace(0, 1, 100)
y = w * x + bias
ax.scatter(df["flipper_length_mm"], df["body_mass_g"], s=0.1)
ax.plot(x, y, color="red", label=f"w={w}")
ax.set_title(f"epoch: {i+1}")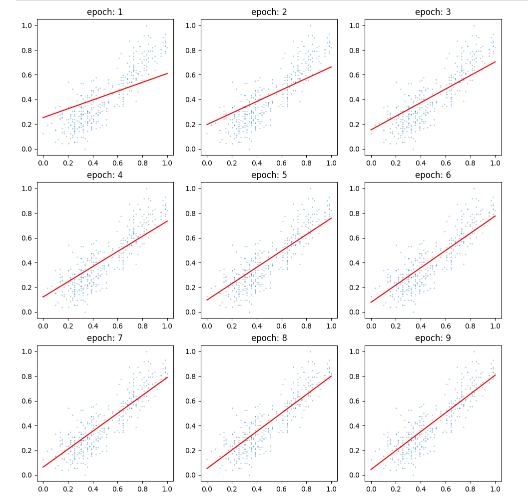
Epoch가 지날 수록 선이 점점 더 데이터를 잘 설명하는 방향으로 기울기와 절편이 조정된다.
