코드를 알아보기 전에 먼저 문제와 알고리즘을 이해하여 스스로의 힘으로 코드를 짜보는 시간을 갖길 바랍니다.
문제 이해하기
숫자의 배치 조합으로 가장 큰 수를 만들어내는 문제입니다.
큰 숫자가 앞쪽에 배치될 수록 조합된 최종 수는 커지게 됩니다.
numbers의 원소는 0 이상 1,000 이하입니다.
그러나 numbers의 원소가 0~9로만 구성되어있지 않으므로 10이상의 숫자를 앞쪽에 배치하면 오히려 최종 숫자가 작아질 수도 있죠. 문제 상의 첫 번째 예제가 그 예입니다.
그렇담 10을 숫자 10이 아닌 1과 0이 나란히 붙어있는 문자열로 생각하면 어떨까요?
문자열의 대소관계는 사전상 더 큰 것을 기준으로 하고 있죠. 두 문자열을 비교할 때 각 문자열의 0번째 문자부터 사전 상으로 더 큰 문자를 가진 문자열이 더 큰 겁니다. 그렇게 봤을 때 "10"의 '1'보다는 '6'이 더 크죠. 그럼 문자열 "10"과 "6"의 대소관계는 "6" > "10"이네요.
그런데 두 번째 예제에서 "3"은 "30"보다 사전 상으로 작지만 "30"보다 앞에 있어야 최종 숫자가 가장 커지게 됩니다. 330이 303보다 크기 때문이죠.
따라서 "3"과 "30"을 비교하는 게 아닌 "3"이 뒤에 있을 때인 "303"과 "3"이 앞에 있을 때인 "330"을 비교한다면 "3"이 어디에 있어야 최종 숫자가 가장 커질지 알 수 있겠습니다.
알고리즘 이해하기
- numbers를 String 배열로 바꿔준다.
- numbers의 문자열 원소들로 sort하되, 비교하는 두 문자열(a, b)이 길이가 다를 경우, a 뒤에 b를 이어 붙이고, b 뒤에 a를 이어 붙인 값으로 sort한다.
(제 벨로그 역사상)역대급으로 간단한 알고리즘이네요! ^0^
모든 원소에 대해서 비교할 두 문자열을 서로 이어 붙여도 문제 풀이에는 지장이 가진 않습니다.
다만 두 문자열의 길이가 다를 경우만 이어 붙인다면 시간 절약이 되어 좋겠죠?
효율성 테스트가 없는 문제이지만 항상 효율성을 신경 써주시는 것이 중요합니다~
tip
- 모든 요소가 0이라면 최종 숫자도 0이어야 할 것입니다.
문제 해결 코드(java)
import java.util.Arrays;
class Solution {
public String solution(int[] numbers) {
String[] nums = new String[numbers.length];
for(int i = 0; i < nums.length; i++)
nums[i] = Integer.toString(numbers[i]);
Arrays.sort(nums, (o1, o2) -> {
if(o1.length() != o2.length()){
o1 = o1 + o2;
o2 = o2 + o1;
}
return o2.compareTo(o1);
}
);
return String.join("", nums).charAt(0) == '0' ? "0" : String.join("", nums);
}
}(잡담) 효율성에 관한 고찰
해당 문제의 다른 분들 코드를 보는데 단순하게 각 요소를 3번씩(각 요소가 1000을 넘지 않음.) 반복한 값을 기준으로 문자열 정렬을 하는 경우에도 문제 해결이 잘 되더라고요!
그게 신기해서 효율성에도 차이가 있는지 확인해봤습니다.
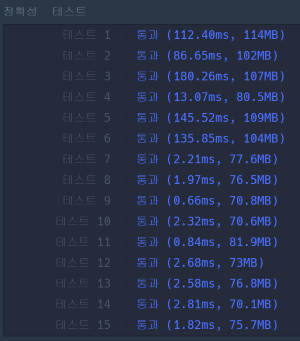
먼저 제가 쓴 코드의 테스트 결과입니다.
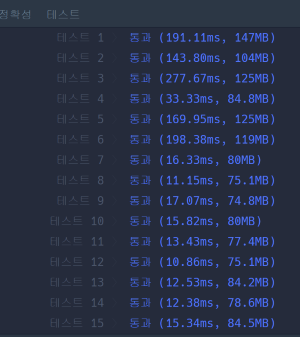
각 요소를 3번씩 반복한 값으로 문자열 정렬을 한 코드의 결과입니다.
큰 차이는 없지만 어느정도 차이가 있네요. 아무래도 각 요소를 3번씩 반복하는 방법은 비교하는 두 문자열이 같은 길이일 때도 3배수의 길이로 늘려 비교하기 때문에 시간이 좀 더 걸리는 것 같습니다. 두 요소를 서로 이은 길이가 3배수보다 작기도 하고요.
오히려 테스트 데이터가 커질 수록 시간 차이는 별로 안 나는 것도 신기하네요~
