📚TL;DR
알고리즘을 공부 안한다고 코딩을 못하는 것은 아니다. 하지만, 알고리즘을 공부하면 컴퓨터에게 더 똑똑하게 일을 시킬 수 있다.
프로그래밍 입문자를 위한 포스팅입니다. 알고리즘과 재귀의 정의, 하노이의 탑 게임의 룰을 알고있다면 더 재미있게 읽으실 것이라고 생각합니다 😊

알고리즘, 알고리즘, 알고리즘
글쓴이는 프로그래밍을 처음 입문 할 당시, 알고리즘 알레르기가 있었다. 물론 기능을 구현하는데 필요한 자료구조와 알고리즘은 제외. 아무튼 글쓴이는 알고리즘은 당장 취업할때나 필요하고, 이후엔 매우 어려운 문제에 봉착하는 경우, 특수한 케이스를 해결하기 위해서 공부하면 될 것이라고 생각했다. 그런데 얼마전에 이를 바꿀만한 경험을 했고, 그 경험을 공유하고자 포스팅을 한다.

프로그래밍 감각과 재귀법
사수님과 점심을 같이 먹고 있었다. 갑자기 질문을 받았다.
사수님 : 입문자가 프로그래밍 감각이 있는지 판단하기 가장 쉬운 방법이 뭔지 아세요?
글쓴이 : 음... 잘모르겠네요
사수님 : 재귀 알고리즘 문제를 풀어보라고 하면 되요
글쓴이 : 어째서죠???
사수님 : 재귀함수를 잘 짜면 연역적으로 사고 할 수 있다는 뜻이거든요 ㅎㅎ

하노이의 탑
사수님에게 설명을 부탁드렸다. 백문이불여일견이라고 알고리즘 문제를 직접 풀어보는게 빠르다고 말하셨다. 여러분도 직접 풀어볼 수 있도록 문제를 내보겠다. 제약 사항을 집중해서 보자.
하노이의 탑
n개의 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓아야 한다.
1. 한 번에 하나의 원판만 옮길 수 있다.
2. 큰 원판이 작은 원판 위에 있어서는 안 된다.
문제
n개의 원판을 모두 옮기는데 필요한 시행 회수를 도출하는 함수를 구현하라.
예시) 3개의 원판을 모두 옮기려면 7번의 시행 회수가 필요하다면hanoi(3) = 7
1. 재귀함수로 구현 할 것.
2. 귀납법을 사용하면 안된다.
귀납법은 사례나 현상에서 부터 일반적인 결론을 이끌어내는 추론 방법이다. 즉 하노이의 탑을 귀납적으로 해결한다고 하면, 직접 게임을 수행 한후, 일련의 과정에서 통용 되는 법칙을 찾을 것이다. 독자들이 글쓴이와 유사하다면, 다음과 같은 과정을 거칠 것이다.
귀납적으로 푼다면
- 우선 원판 직접 게임을 시행 해볼까?
hanoi(1) = 1일 것이고hanoi(2) = 3이고hanoi(3)은 몇이지?- 머리속에서 하기 어렵군 그림을 한번 그려보자.
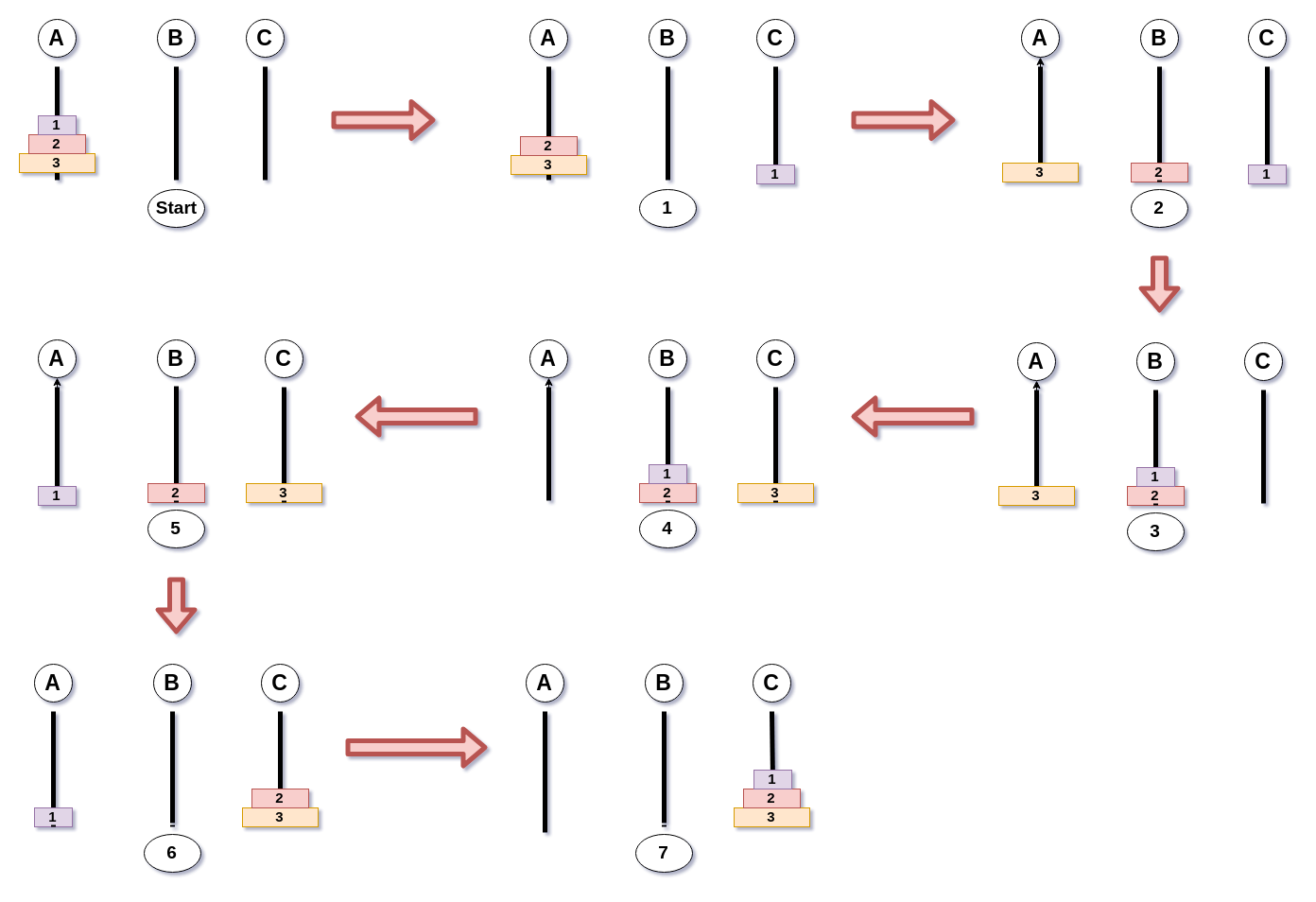
hanoi(3) = 7이군. 이제 통용되는 로직을 생각해보자. 우선 맨 위에 있는 원판을 c로 이동시키고, 그 다음에는...

귀납 멈춰!!!✋
재귀법의 문제 해결 방법
1. 일정 조건이 만족 되면 자기 자신을 호출하지 않는다. (종료조건)
2. 자기 자신을 호출하면 할 수록 1번의 조건에 가까워져야한다. (종료조건으로 수렴)
3. 1번에 부합하지 않는다면, 2를 이행하는 행동을 하고 자기자신을 호출한다. (재귀)
정신이 멍해져버렸다. 정신을 가다듬고 다시 생각 해보자. 문제에 재귀법을 사용하라 했으니 당연히 재귀함수를 짜야할 것이다. 재귀함수에는 종료조건이 필요하다. 머리를 식힐겸 함수를 한번 짜보자.
def hanoi(n):
# 원판이 1개라면 1회의 시행으로 게임이 끝난다
if n == 1:
return 1오케이 이건 금방 생각 할 수 있다. 그러면 어떻게 종료조건으로 수렴 시키면 좋을까?
연역적으로 푼다면
연역법은 일반적으로 알려진 이론을 어떠한 현상에 대입시켜 이에 대한 결론을 도출해내는 방법이다. 사전적 개념은 '어떤 명제로부터 추론 규칙에 따라 결론을 이끌어 내는 것'을 말한다. 글쓴이와 같이 문제를 다시 살펴보자.
- 당연하지만, 사람이 풀라고 만든 문제일 것이다.
- 재귀법을 사용하라고 했다, 따라서 재귀법으로 풀 수 있는 문제일 것이다.
- 재귀함수는 자기자신을 호출한다, 반복적으로 함수가 실행된다는 것이다.
- 즉 하노이의 탑 게임은, 반복적으로 같은 행동을 수행하면 클리어 가능한 게임이다.
사실 연습문제 였다. 축하합니다. 하지만 덕분에 당신은 연역법을 마스터했습니다. 이제 하노이의 탑 게임의 룰을 생각해보자
- 작은 원판 위에 큰 원판이 있을 수 없다.
- 따라서, 목적지 기둥에는 가장 큰 원판 부터 순서대로 원판이 쌓여야한다.
- 즉, 목적지 기둥에 가장 큰 원판을 먼저 옮겨야한다.
- 그러기 위해서는 가장 큰 원판을 제외한 모든 원판을 중간 기둥으로 옮겨야한다.
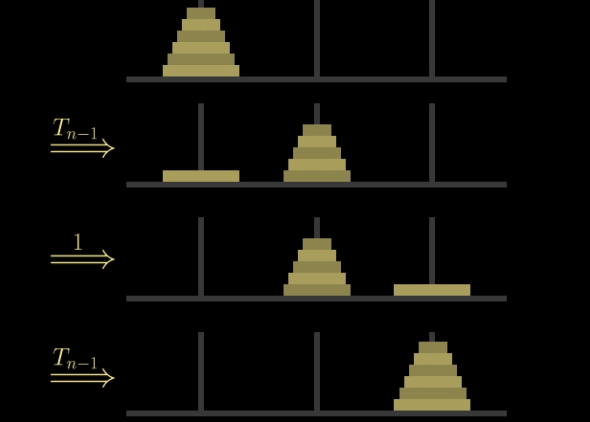
띠띠용!💡 가장 큰 원판을 제외한 원판을 중간 기둥으로 옮기는 것은
1개 적은 원판 개수로, 하노이의 탑 게임을 하는 것과 동일하다!!! 반복작업을 찾았다!!!
수식으로 표현하면 다음과 같다. 이걸 그대로 함수에 적용하면 된다.
hanoi(n) = 2 * hanoi(n-1) + 1빨리 정답 알려주세요

def hanoi(n):
# 원판이 1개라면 1회의 시행으로 게임이 끝난다
if n == 1:
return 1
# 수식을 그대로 집어 넣자
return 2 * hanoi(n-1) + 1뭔가 엄청 간단해 보인다. 게임 클리어에 필요한 시행 회수를 계산하는 함수를 만들긴 했는데, 어떻게 가장 짧은 회수로 게임을 클리어하는 방법 자체는 모르겠다. 하노이의 탑 그게 뭔데? 그거 어떻게 하는 건데?
모르는게 정상이다
극단적인 예시를 들어보자. 물리엔진을 만든 개발자가 있다. 당신은 그 개발자에게 다음과 같은 질문을 했다.
님이 만드신 물리엔진에서 젠가를 쌓아놓고 거기다가 공을 차면 어떻게 되나요?
다음 중 어느 대답이 더 신빙성이 있는가?
- 그러한 경우 제가 이렇게 저렇게 동작하게 만들어 놓았기 때문에 다음과 같은 결과가 나올 것입니다...
- 시뮬레이션을 돌려봐야 알 것 같은데요. 해당 케이스에 적용 되는 법칙은 다음과 같습니다...
글쓴이 같으면 2번 대답이 더 신빙성이 있을 것 같다. 물론 글쓴이가 물리엔진을 잘안다는 것은 아니고. 물리엔진 처럼 복잡한 프로그램을 만들면서, 모든 케이스를 일일히 직접 생각해가면서 만드는게 편할까. 통용이 가능한 공식의 모음으로 생각하면서 만드는게 편할까? 전자와 후자 중 어느 경우가 에러가 더 많을까?
컴퓨터에게 생각을 이양하자

컴퓨터는 똑똑하다. 계산을 실수하는 일도 없고. 기억력도 사람보다 좋다. 하지만 컴퓨터는 멍청하기도 하다. 당연하지만, 시킨일 밖에 못한다. 컴퓨터에게 명령하기 위해서는 명확한 룰을 정해서 프로그래밍 언어로 실수 없이 정리 해줘야한다. 효율적으로 프로그램을 짜기 위해서는 컴퓨터에게 현명한 명령을 내려야한다. 말은 쉽지 현명하게 명령을 내리는 것은 겁나 어렵다. 그래서 알고리즘이 어렵다.
하지만 현명하게 명령을 내릴 수 있다면 어려운 문제를 해결 할 수 있다. 애초에 사람이 쉽고 빠르게 해결할 수 있는 문제였으면 프로그램을 작성할 필요가 희박하다고, 글쓴이는 생각한다. 뭔가 하노이의 탑 알고리즘을 이야기하다가, 왜 프로그래밍을 하는지에 대해 까지 급발진 한 것 같다. 정리 하자면 다음과 같다.

알고리즘이란 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것 또는 계산을 실행하기 위한 단계적 절차를 의미한다. 알고리즘 문제를 푸는 것은 컴퓨터에게 생각 또는 작업을 이양하는 것의 연습이다.

