---

제 3장. 기초 통계학

📌1. 논리적사고

연역적 추론

• 보편화된 원리로부터 개별적인 결론을 도출
  

귀남적 추론

• 개별적인 사례로부터 보편화된 원리를 도출
  

일반화의 오류

몇 가지 사실만으로 일반화된 규칙을 정하는데서 발생할 수 있는 오류
성급한 일반화(영어: hasty generalization) 또는 성급한 일반화의 오류란 몇 개의 사례나 경험으로 전체 또는 전체의 속성을 단정짓고 판단하는 데서 발생하는 오류이다.
불확실한 증거를 기반으로 둔 귀납적 일반화에 도달하는데 귀납적 오류의 논리적 오류를 일컫는 말이다.

---

📌2. 통계적사고

통계적 추론

• 귀납적 추론으로부터 가설을 세우고
• 가설을 검증함으로써 일반화된 원리로 신뢰도를 높이는 사고 방식
• 표본으로부터 얻은 결론을 전체 모집단에 일반화하는 과정

통계학의 분류

통계학의 기본 용어

---

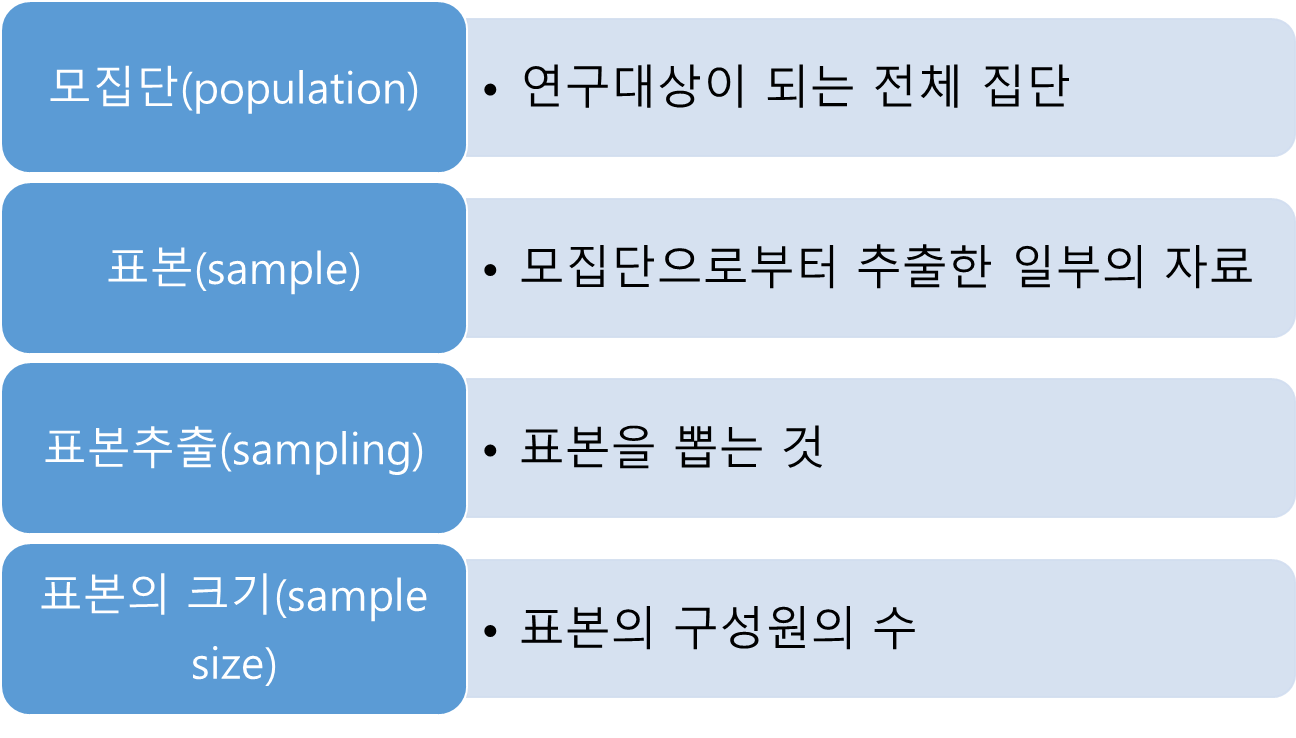
전수조사와 표본조사

🎯표본조사

• 1. 표본이 가져야 할 가장 중요한 성질은 대표성
• 2. 비용과 시간이 적게 들어 경제적
• 3. 짧은 시간 내에 필요한 정보 흭득
• 4. 전수조사에서 발생하는 착오 최소화
• 5. 전수조사가 불가능한 경우에 편리

---

📌3. 통계적 연구 방법

📌통계적 연구 방법 - 실험

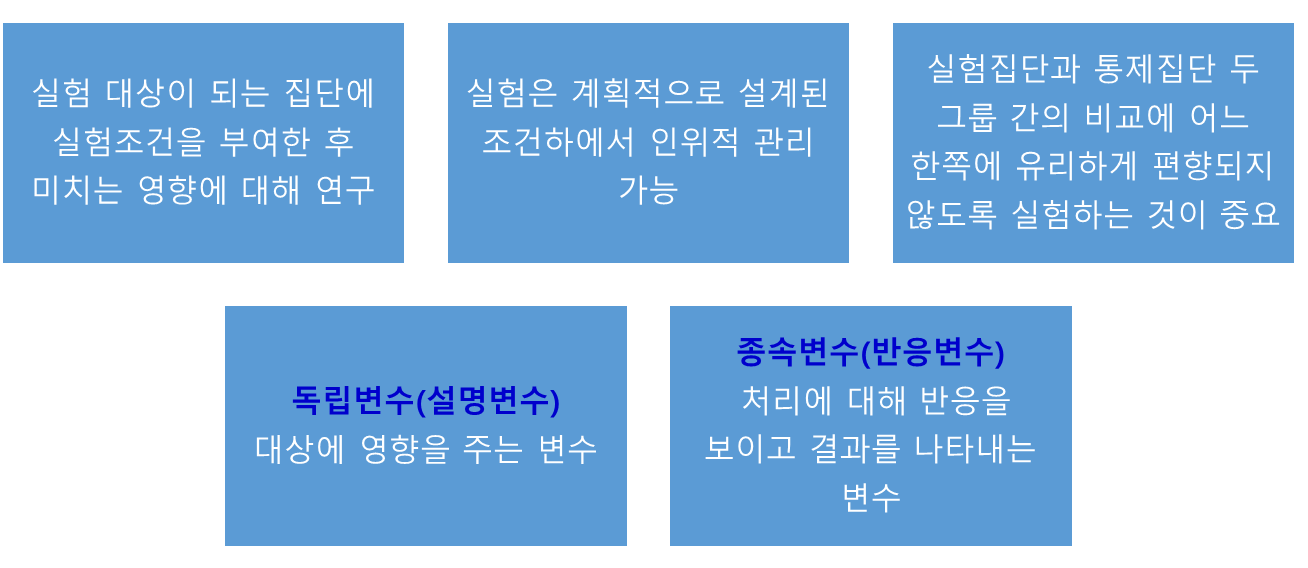
📌통계적 연구 방법 - 관찰

📌통계적 연구 방법 - 조사

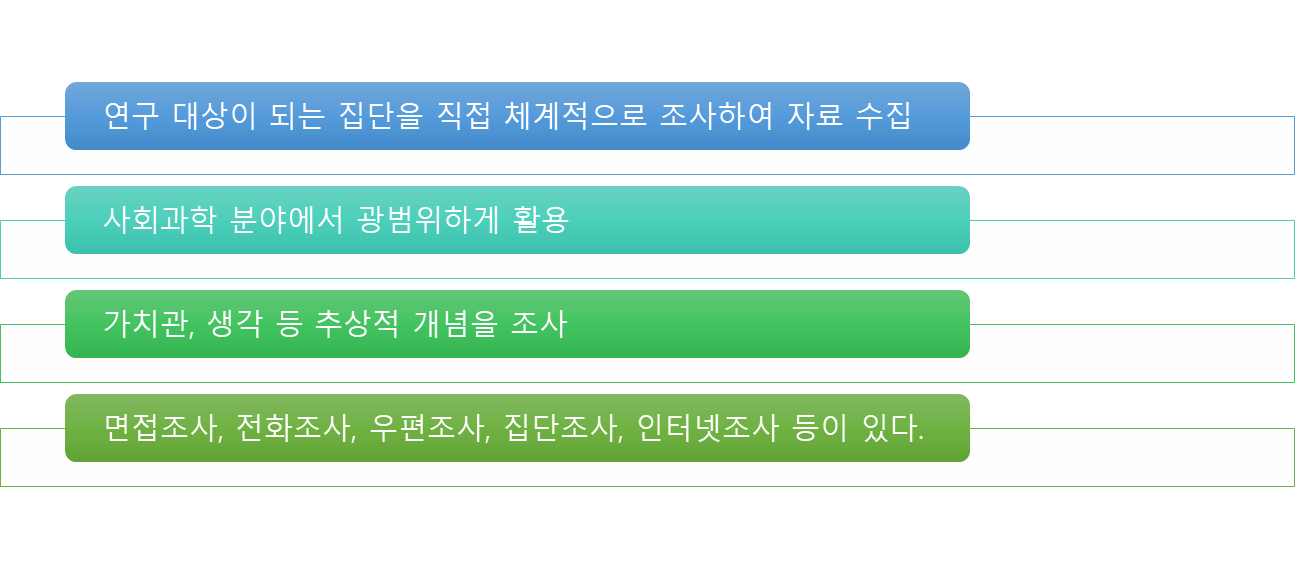
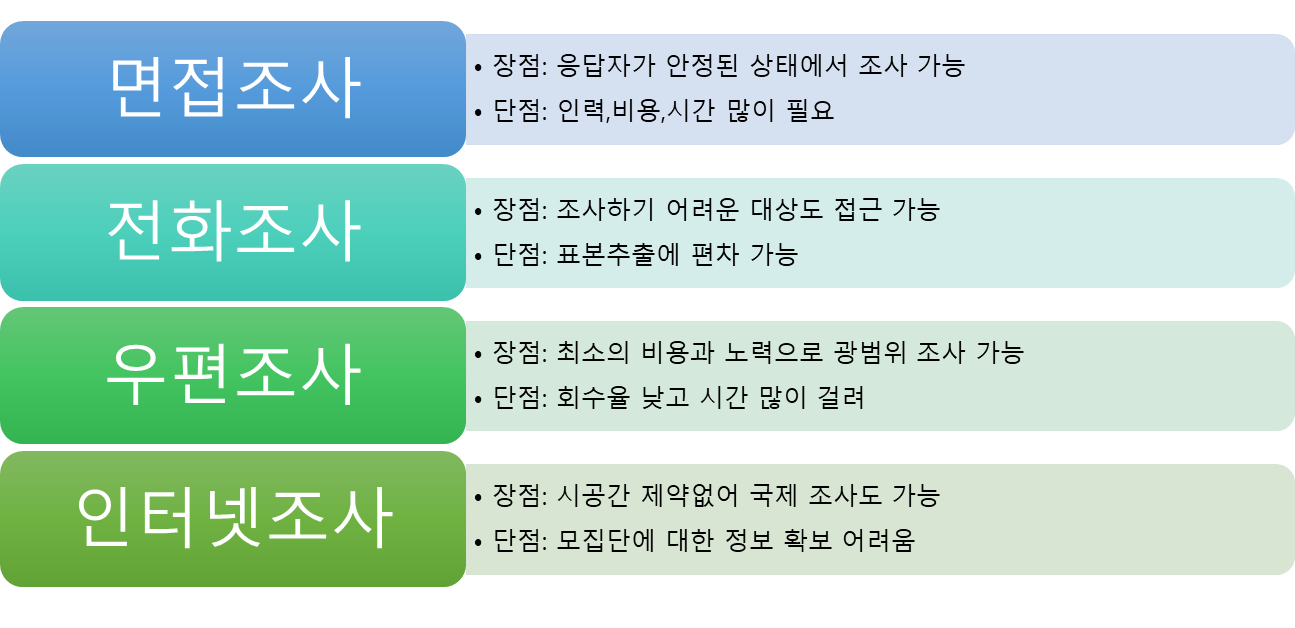
조사방법의 장단점

📌통계적 연구 방법 - 내용분석

---

통계학의 왜곡 사례

표본추출의 오류

• 1936년 미국 대통령 선거 여론 조사
• 현직 대통령 루즈벨트(민주당) vs 랜든(공화당)
• 리터러리다이제스트(Literary Digest)사
  • 구독자 명부, 전화번호부, 자동차등록부에서 1,000만명 추출
  • 230만명 응답
  • 57%가 랜든이 이길 것으로 예측
  • BUT 루즈벨트가 62%로 당선
• 이 결과는 역사에 길이 남을 잘못된 여론조사의 사례
• 문제점
  • 표본이 모집단을 대표하지 못함
  • 당시 잡지구독자, 전화·자동차 보유자는 부유층에 속함

---

📌4. 표본추출법 - 확률표본추출법

표본추출법 - 📌단순임의추출법

표본추출법 - 📌층화추출법

표본추출법 - 📌집락추출법

표본추출법 - 📌계통추출법

---

📌비확률표본추출법

• 보행자 조사법

  • 길가는 보행자를 대상으로 조사
  • 가장 쉬운 방법이지만 결과를 일반화하기는 어려움

• 판단추출법

  • 전문가 집단의 면접 조사 방법
  • 연구 내용을 잘 알고 있는 전문가를 주요 응답자로 선정

• 눈덩이 추출법

  • 소수의 적절한 응답자 조사
  • 응답자들의 추천으로 새로운 응답자 모집

• 할당추출법

  • 모집단의 구성 비율이 표본에 반영되도록 할당
  • 각 그룹 별 조사는 조사원의 판단에 따라
  • 층화표본추출법과 유사(확률/비확률)

📌비교

확률표본추출법

표본틀(sample frame)이 있다
랜덤(random) 추출
모수 추정에 편의(bias) 없음
표본 결과 일반화 가능
시간과 경비 많이 소요

비확률표본 추출법

표본틀(sample frame)이 없다
인위적인 표본 추출
편의 존재 가능
일반화 제약
시간, 경비 절약

---

통계학 및 자료의 분류

통계학 및 자료의 분류 - 값의 형태에 따른 분류

---

📌6. 질적 자료의 정리

도수분포표

메타정보

그래프(막대, 원)

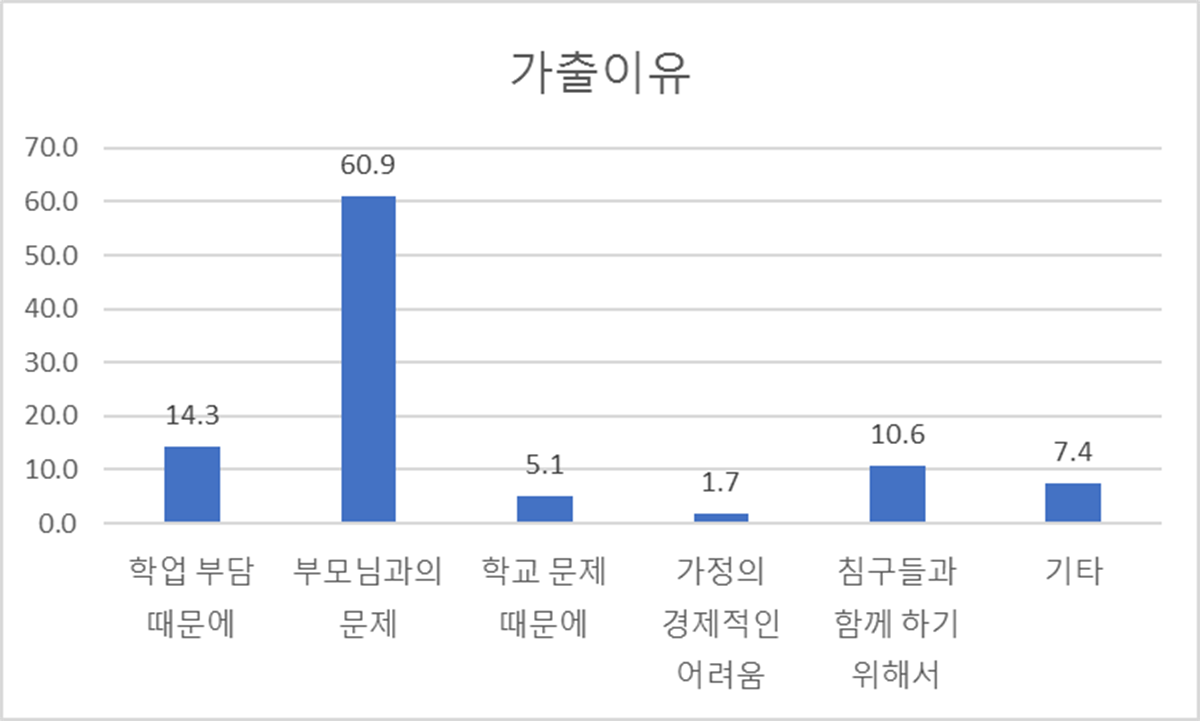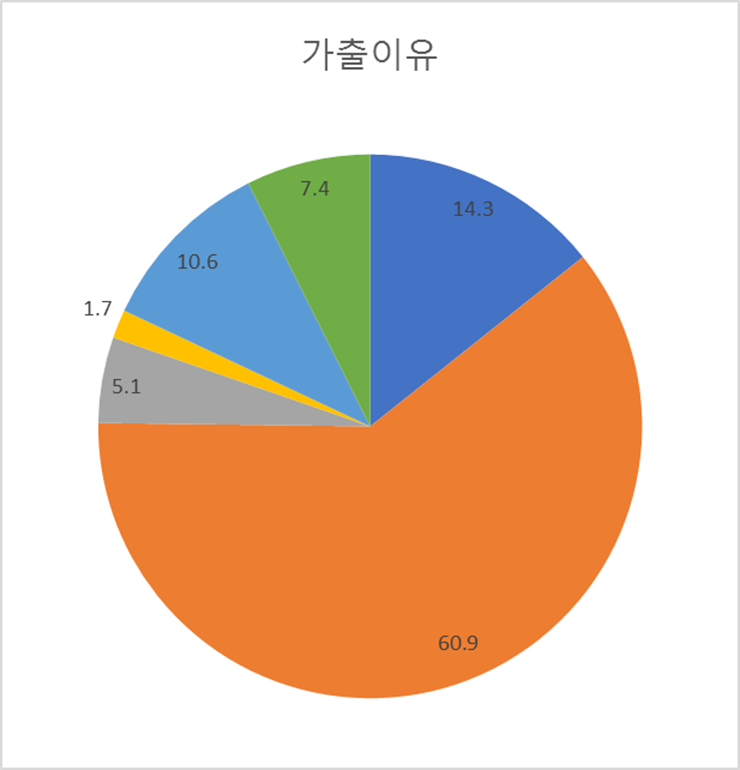누적막대그래프

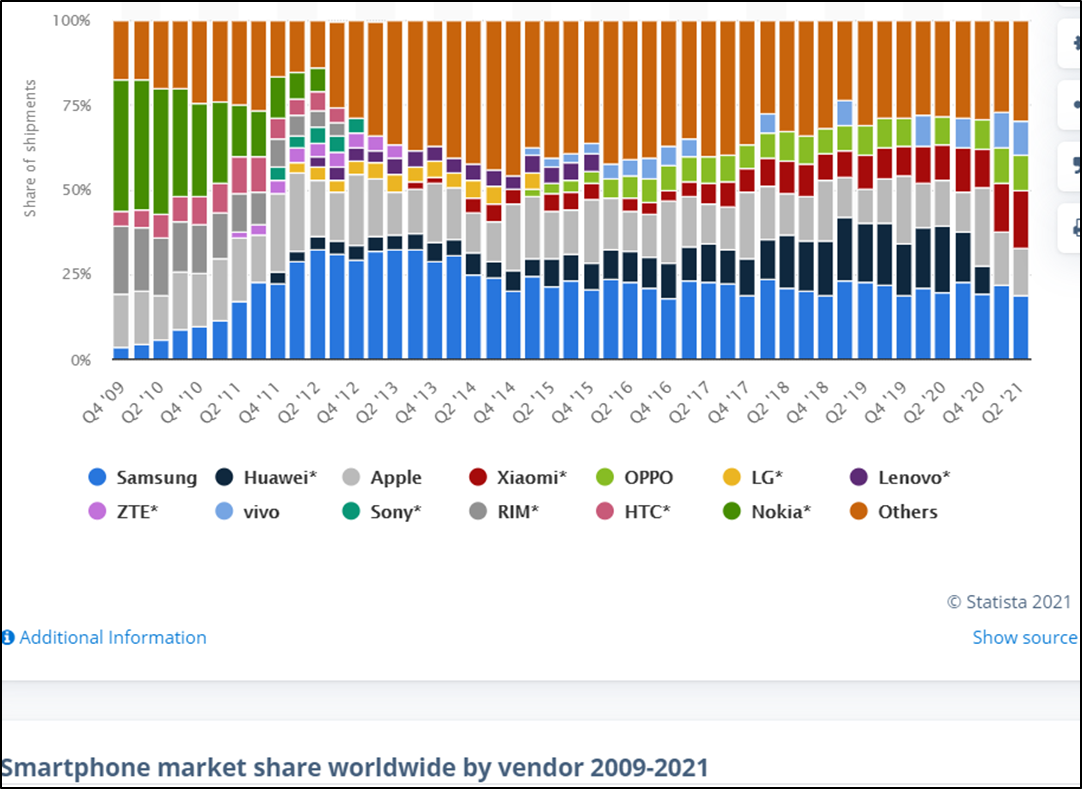
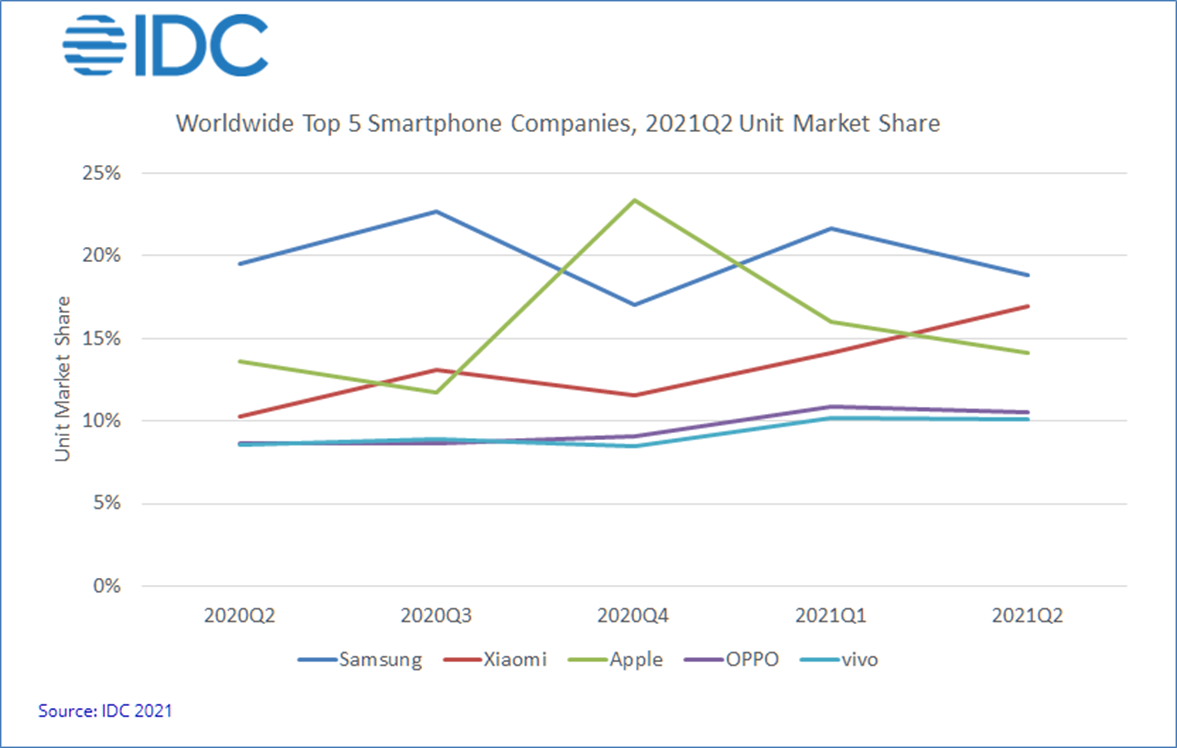
시계열 그래프

---

과제 2

과제 제출 방법
MS word 파일로 작성하여 TLS에 탑재 - 한 파일에 작성
파일이름: 학번-이름-데이터과학-과제2.docx
제출기한: 9월 20일(금) 20:00까지

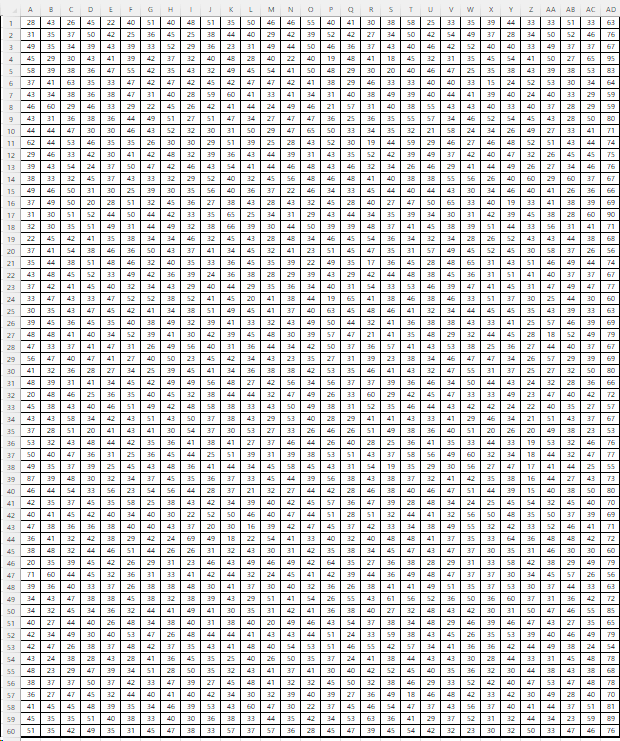
2-1 그림에 1800개의 자료가 있다. 이 자료의 평균을 추정(예측)하는 방법에 대하여 설명하시오. 가능하면 (추정)값도 제시하시오.

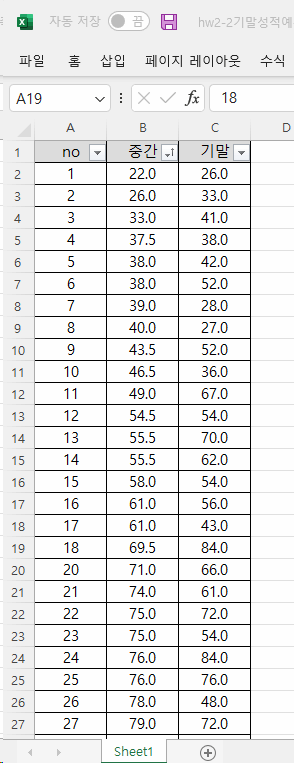
2-2. 다음은 어느 클래스의 중간고사, 기말고사 성적에 대한 자료이다. 중간고사에서 70점을 맞은 학생이 군입대로 기말고사를 치르지 못하였다. 기말고사 점수를 부여한다면 얼마가 적절한지 그 방법에 대하여 설명하시오. 가능하면 적절한 기말고사 성적도 제시하시오.
파일: hw2-2기말성적예측-2022.xlsx

2-1

import random
import math
import statistics

# 모집단에서 표본 추출
def get_samples(population_range, sample_size):
    return [random.randint(population_range[0], population_range[1]) for _ in range(sample_size)]

# 표본 평균 계산
def calculate_sample_mean(samples):
    return statistics.mean(samples)

# 표본 표준편차 계산
def calculate_sample_std(samples):
    return statistics.stdev(samples)

# 신뢰구간 계산
def calculate_confidence_interval(sample_mean, sample_std, sample_size, confidence_level=0.95):
    # 자유도가 49일 때의 t-값 (95% 신뢰수준)
    t_value = 2.01
    margin_of_error = t_value * (sample_std / math.sqrt(sample_size))
    return (sample_mean - margin_of_error, sample_mean + margin_of_error)

# 메인 실행 부분
if __name__ == "__main__":
    population_range = (10, 90)  # 모집단의 범위
    sample_size = 50  # 표본 크기

    # 표본 추출
    samples = get_samples(population_range, sample_size)
    print("추출된 표본:")
    print(samples)

    # 표본 평균 계산
    sample_mean = calculate_sample_mean(samples)
    print(f"\n표본 평균: {sample_mean:.2f}")

    # 표본 표준편차 계산
    sample_std = calculate_sample_std(samples)
    print(f"표본 표준편차: {sample_std:.2f}")

    # 95% 신뢰구간 계산
    confidence_interval = calculate_confidence_interval(sample_mean, sample_std, sample_size)
    print(f"95% 신뢰구간: ({confidence_interval[0]:.2f}, {confidence_interval[1]:.2f})")

무작위 표본 추출: 전체 1800개 중 일부(예: 50-100개)를 무작위로 선택한다.

표본 평균 계산: 선택된 표본의 평균을 계산한다.

신뢰구간 설정: 표본 평균을 중심으로 신뢰구간을 설정하여 모집단 평균을 추정한다.

약 6번을 실행한 결과

45~51사이의 평균을 가질것이다.

2-2

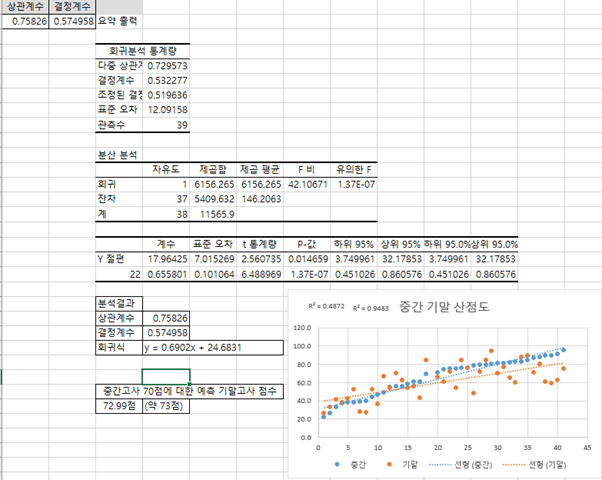
1. 상관계수
   =CORREL(B2:B41,C2:C41) 함수의 결과가 0.75826
   상관계수 0.75826은 중간고사와 기말고사 점수 사이에 강한 양의 상관관계가 있음을 나타냅니다.
2. 결정계수 (R 제곱, R-squared):
   R 제곱 = 0.75826^2 = 0.5749 (약 0.5750 또는 57.50%)입니다.
3. 회귀식: y = 0.6902x + 24.6831 (y: 기말고사 점수, x: 중간고사 점수)

기말고사 예측점수 -> 73점