📌분산과 표준편차

• 편차 = 자료 - 평균

• 분산(𝜎^2): 편차의 제곱의 평균 -> 𝜎^2=1/𝑛 Σ(𝑋−𝑋 ̅ )^2

• 표준편차(𝜎): 분산의 양의 제곱근

🎯 표준편차 특징

• 표준편차를 사용하는 이유: 단위가 같음
  (분산은 자료의 제곱)

• 표준편차가 작을 수록 자료는 평균 주위에 몰려 있음

• 표준편차는 범위와 달리 모든 자료를 이용하기 때문에 주어진 정보 충분히 활용

• 이상점에 의해 영향이 있음

🎯 모표준편차(𝜎)와 표본표준편차

---

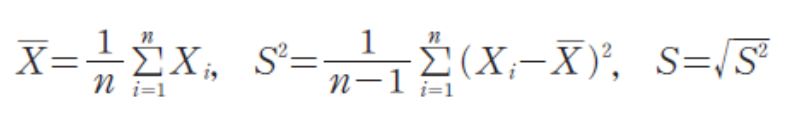
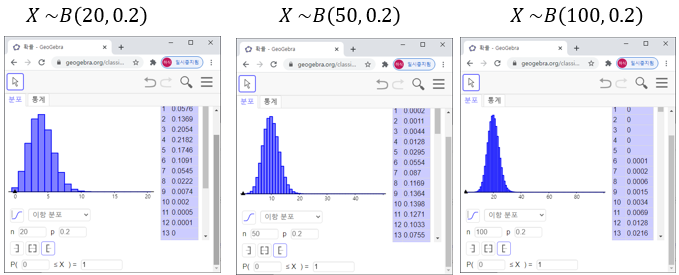
🎯 이항분포 -> 정규분포곡선에 수렴(대칭인 종모양)

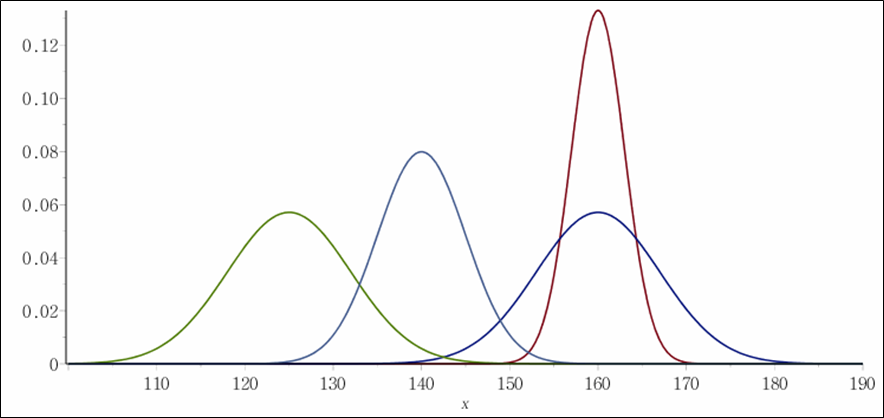
🎯 정규분포 - Normal distribution

평균이 𝜇, 표준편차가 𝜎인 정규분포를𝑋∼𝑁(𝜇, 𝜎^2 )으로 나타낸다.

---

• 자료가 정상적인 분포를 따를 때 자료의 99.73%는 𝜇±3×𝜎 범위 내에 존재한다.

• 모집단의 분포가 𝑁(170, 8^2)일 때이 모집단에서 선택한 1명의 키는 (170−3×8, 170+3×8)=(146, 194)

---

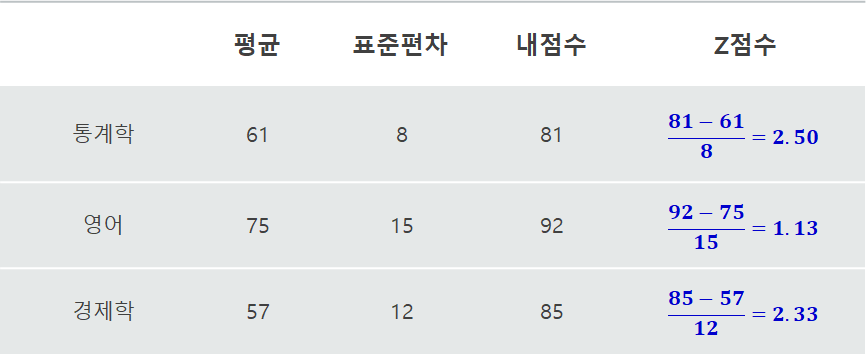
📌자료의 표준화

자료의 표준화 - Z 점수

자료의 표준화 - T 점수

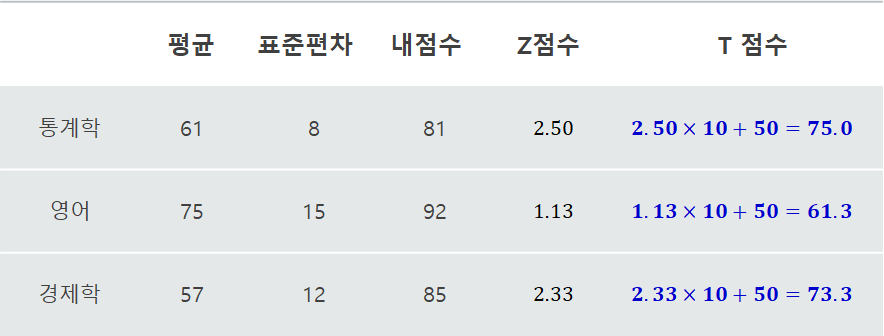📌제 4장 추론통계학

• 추정
  점추정
  구간추정(신뢰구간)
• 검정
  통계적 가설검정
• 통계적 분석 – 이변량의 연관성
  교차분석
  분산분석(Analysis of variance)
  회귀분석(Regression)

🎯확률표본과 통계량

• 확률표본
  모집단으로부터 추출한 표본
  X1, X2, X3, ......, Xn
• 표본평균
  x̄ = 1/nΣX
• 표본분산
  S^2 = 1/n-1 Σ(Xi - x̄ )^2

---

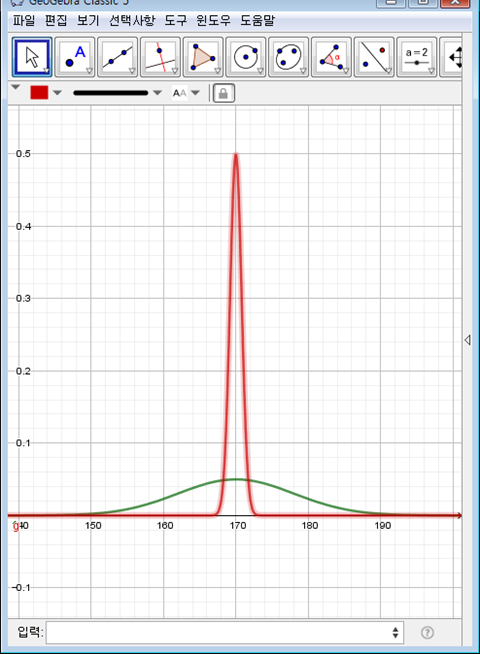
🎯표본평균의 분포

모집단이 평균이 𝜇"이고, " 표준편차가" " σ인 정규분포를 따를 때

𝑋 ̅∼𝑁(𝜇, 𝜎^2/𝑛)

🎯중심극한정리

모평균이 𝜇, 모표준편차가 𝜎일 때, 모집단의 분포에 관계없이 표본의 크기 𝑛이 충분히 클 때 표본평균 𝑋 ̅는 근사적으로 정규분포를 따른다.

• 즉, 𝑋 ̅≈𝑁(𝜇,𝜎^2/𝑛)