A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction
논문 리뷰
시계열 data 예측을 attention을 적용한 논문,
Dual-Stage Attention 개념에 대한 공부
1. 소개
시계열 예측을 수행하기 위해 많은 연구가 있음.
그 중에서도 예측하고자 하는 변수(이하 target series)와 외생 변수(이하 driving series)들을 함께 사용하여 비선형 mapping function을 학습하고자 하는 NARX(Nonlinear Autoregressive Exogenous) 모델에서는 attention 기법을 사용한 RNN 기반의 인코더-디코더 네트워크가 SOTA라고 알려져 있다.
해당 논문에서 SOTA NARX 모델은
RNN 기반의 인코더-디코더 네트워크는 input sequence가 길어질 수록 모델 성능이 하락하는 문제점과, 시계열 예측에 있어 복수의 driving series 변수들 중 target series를 예측하는 데 있어 중요한 변수가 무엇인지 파악할 수 없다는 문제점을 지적하였다.
위의 문제점을 해결하기 위해 해당 논문은 DARNN이라는 Attention 메커니즘을 제안하는데, 이는 RNN 기반 인코더-디코더에 네트워크에 적용함으로써 보다 나은 성능을 얻을 수 있다.
2. 모델
DUAL-STAGE ATTENTION-BASED RNN
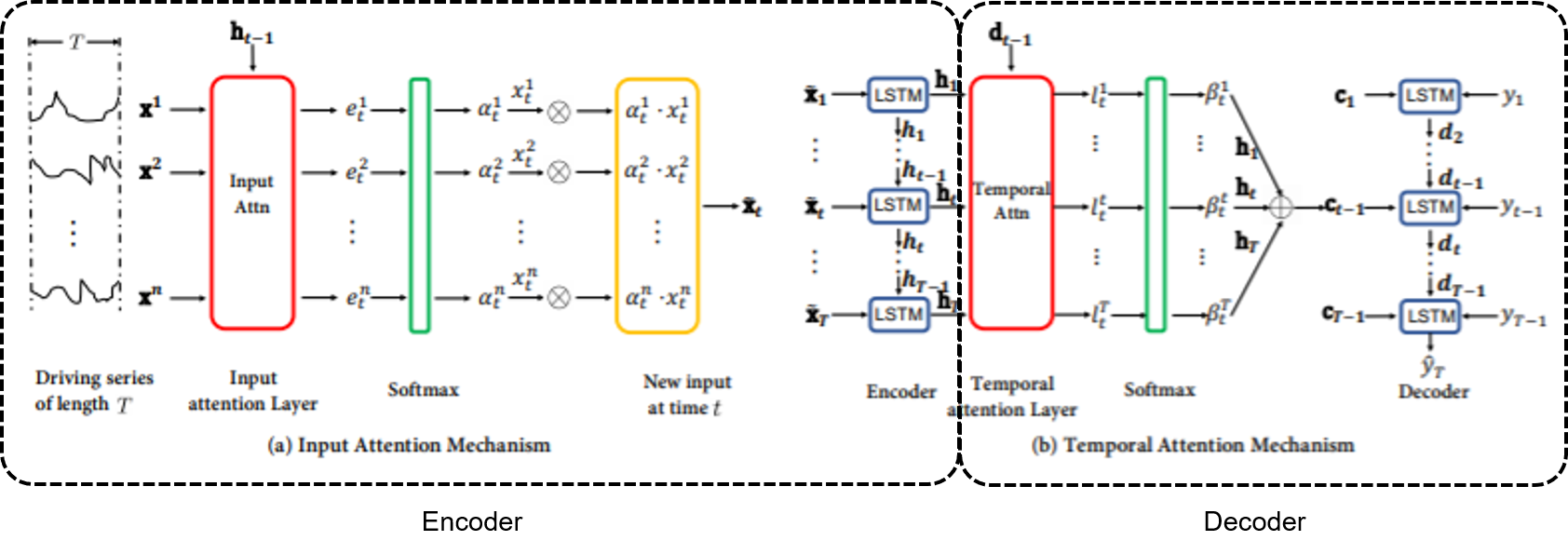
- 순환신경망(여기선 LSTM) network 기반의 encoder - decoder network.
- encoder는 이전 encoder의 은닉 상태를 참고하여 각 시점(timestamp)에서 target series와 연관이 가장 큰 driving seriers를 파악하는 attention 스코어 계산(a)
- decoder는 이전 decoder의 은닉 상태를 참고하여, 전체 시점 중에서 target series와 연관이 가장 큰 encoder와 연관이 가장 큰 은닉상태가 무엇인지 파악한다.(b)
encoder에서 relevant driving series를 선택하기 위해 이루어지는 attention 매커니즘을 Input attention,
decdoer에서 relevant encoder hidden state를 선택하기 위해 이루어지는 attention 매커니즘을 Temporal Attention이라함
- input data : T(timestamp) 동안의 n개의 driving seriers와 n-1개의 target series로 이루어진 텐서
- output data : T(timestamp)에서의 target series
이 모델이 해결해야할 문제는
1. n개의 driving series
2. n-1 target series가 주어졌을 때
3. 그 다음 step에서의 target series가 무엇인지 예측하기
이 문제들을 해결하기 위해서 해당 모델은 2가지 단계의 attention 메커니즘을 적용할 것. 회귀 문제를 해결하기 위해 loss function으로 MSE loss를 활용한다.
Model - Encoder
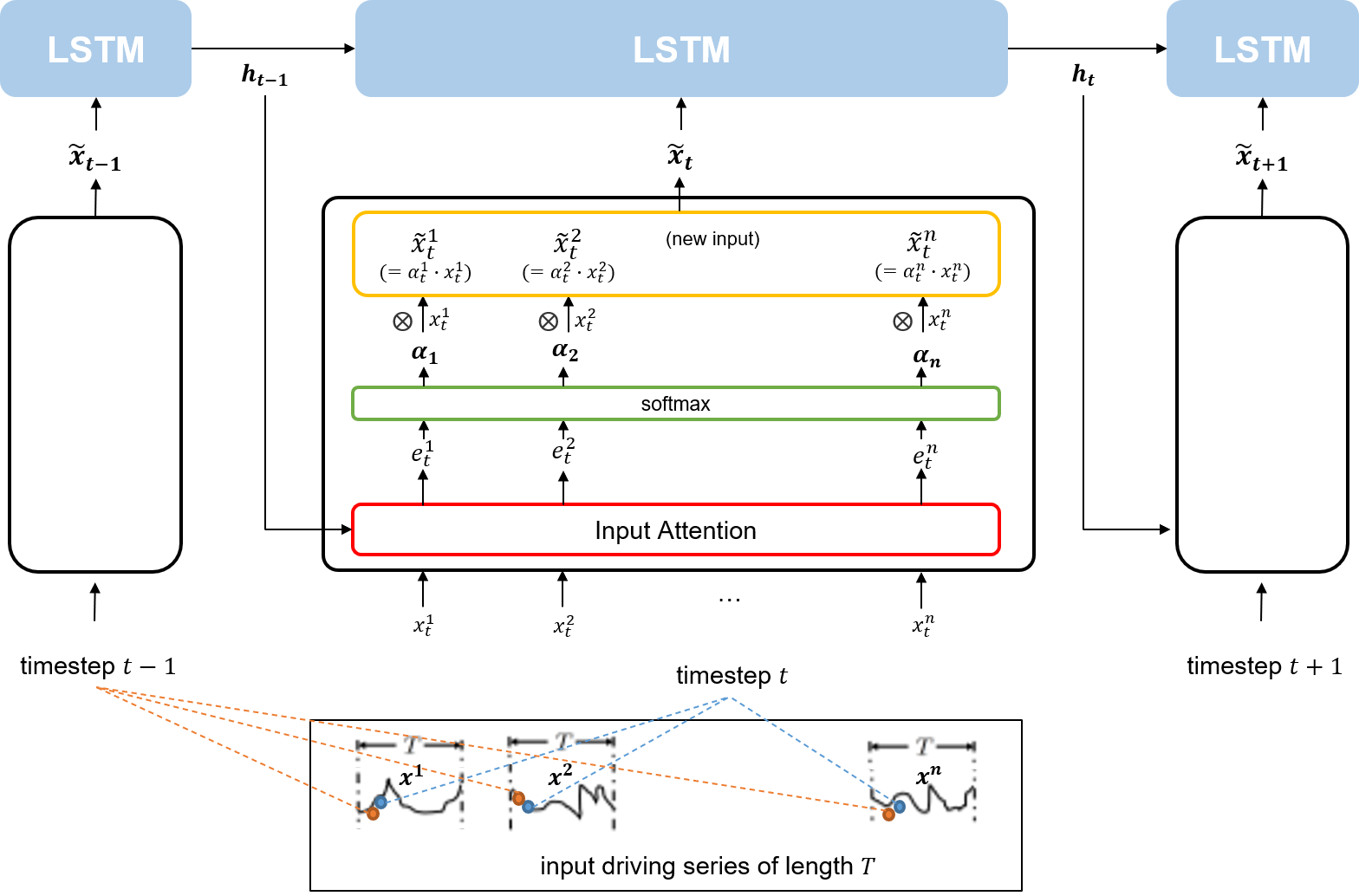
Encoder에는 T만큼의 timestamp 길이를 갖는 n개의 driving series가 input으로 들어가고, 이후 Encoder는 각 timestep에서 n개의 driving series를 대상으로 Input Attention 매커니즘을 적용한 새로은 input vector를 만들어 LSTM셀에 주입.
이 때, 만들어진 새로운 input vector은 이전 LSTM 셀에서의 hidden state를 참고해 attention weight를 적용한 것.
즉, 직전 timestep에서 hidden state와 얼마나 연관성이 높은가가 새로운 input vector에 적용되어 있는 것이다.
Model - Decoder
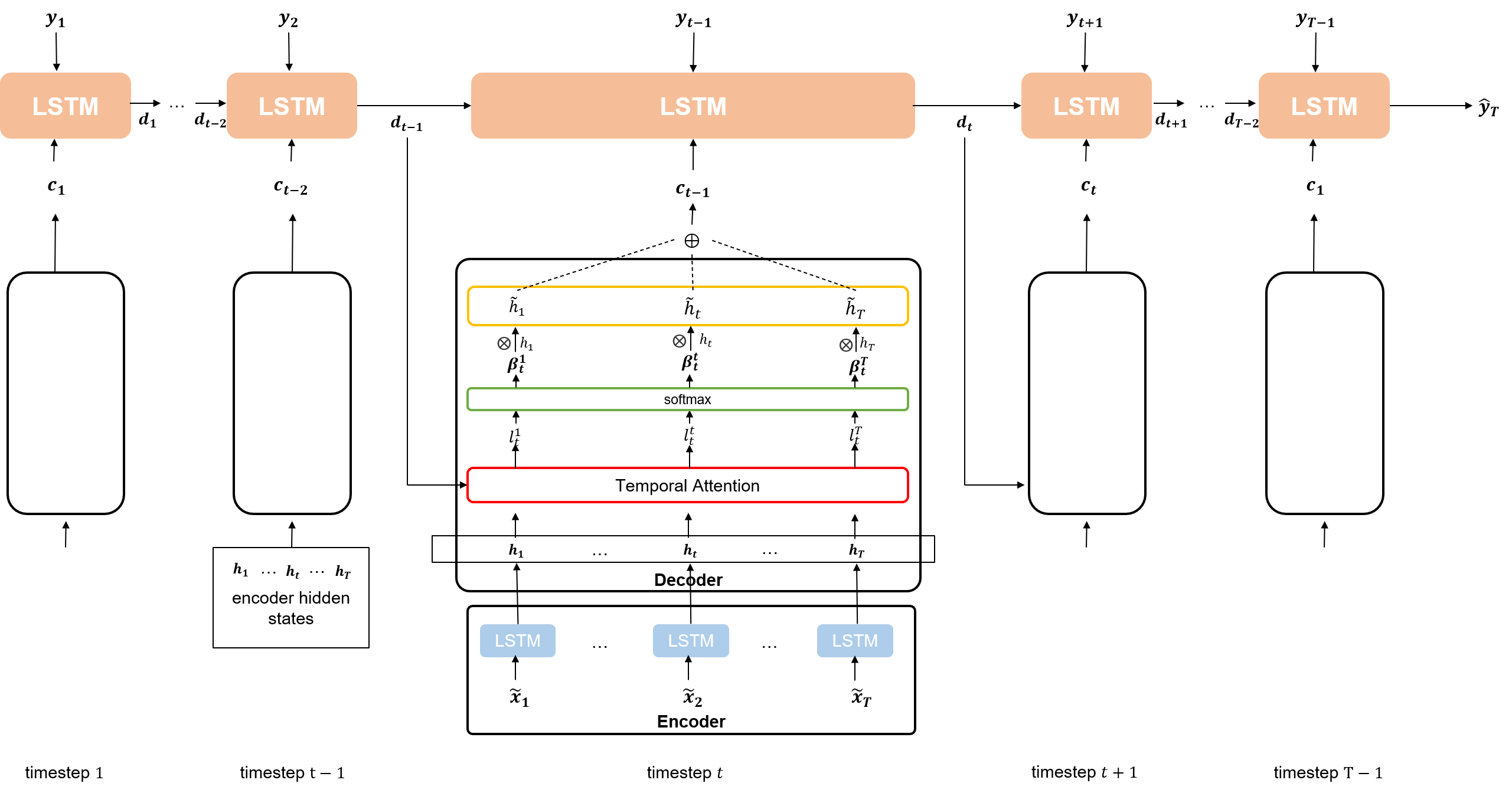
Decoder에는 Encoder의 LSTM에서 나오는 각각의 hidden state에 대해 Temporal Attentin 매커니즘을 적용해 새로운 context vector를 만든다. 그리고 주어진 T-1개의 target series와 context vector를 합하여 LSTM셀에 주입한다. 이 때, 만들어진 새로운 context vector은 이전 Decoder의 LSTM 셀을 참고해 T개의 Encoder hidden state중 어떤 것과 가장 연관성이 높은지를 계산한 attention weight를 적용한 것이다.
즉 요약하면, 직전 timestep에서 Decoder의 hidden state와 연관성이 얼마나 높은지 context vector에 적용되어 있는 것이다.