백준 - 14621번 : 나만 안되는 연애(C++)

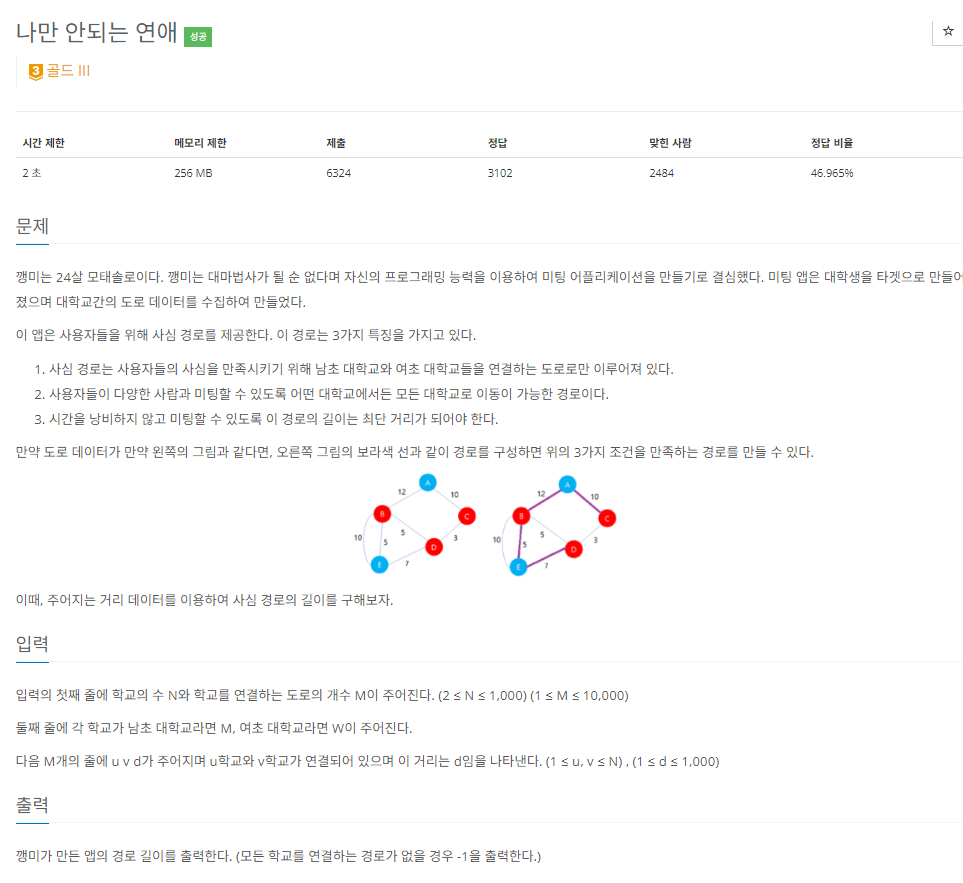
풀이 방법 : 최소 신장 트리

어찌 보자면 전형적인 MST 문제, 입력으로 주어진 경로들 중 남초 대학끼리 잇는 경로와 여초 대학끼리 잇는 경로들을 제외한 경로들을 가지고, 유니온-파인드 알고리즘을 이용하여 최소신장트리를 구성해주면 된다.

최소신장트리를 구성할 수 있는지 없는지는 모든 과정이 끝난 뒤 사용된 경로의 수가 N-1개인지 아닌지 확인하면 된다. 그래프에서 모든 정점을 이을 수 있는 최소 간선의 수는 N-1이기 때문이다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct EdgeInfo
{
    int Src;
    int Dest;
    int Dist;
};

struct cmp
{
    bool operator() (const EdgeInfo& Src, const EdgeInfo& Dest)
    {
        return Src.Dist < Dest.Dist;
    }
};

int Parent[1001] = {};

int FindParent(int Num)
{
    if (Parent[Num] == Num)
        return Parent[Num];

    else
    {
        return FindParent(Parent[Num]);
    }
}

bool IsConnected(int Src, int Dest)
{
    int SrcParent = FindParent(Src);
    int DestParent = FindParent(Dest);

    if (SrcParent == DestParent)
        return true;

    else
        return false;
            
}

void ConnectSchool(int Src, int Dest)
{
    int SrcParent = FindParent(Src);
    int DestParent = FindParent(Dest);

    Parent[DestParent] = SrcParent;

}

int main()
{
    cin.tie(nullptr);
    cout.tie(nullptr);
    ios::sync_with_stdio(false);

    int N, M;
    cin >> N >> M;
    vector<char> vecS(N + 1);
    for (int i = 1; i <= N; ++i)
    {
        Parent[i] = i;
        cin >> vecS[i];
    }

    vector<EdgeInfo> Graph;

    for (int i = 0; i < M; ++i)
    {
        EdgeInfo Info;
        cin >> Info.Src >> Info.Dest >> Info.Dist;
        if (vecS[Info.Src] == vecS[Info.Dest])
            continue;
        
        Graph.push_back(Info);
    }

    sort(Graph.begin(), Graph.end(), cmp());

    int ConnectCnt = 0;
    int MinDist = 0;

    int Size = Graph.size();
    for (int i = 0; i < Size; ++i)
    {
        if (ConnectCnt == N - 1)
            break;

        EdgeInfo Cur = Graph[i];

        if (!IsConnected(Cur.Src, Cur.Dest))
        {
            ConnectSchool(Cur.Src, Cur.Dest);
            MinDist += Cur.Dist;
            ++ConnectCnt;
        }
    }

    if (ConnectCnt == N - 1)
        cout << MinDist;

    else
        cout << -1;
}