백준 - 20529번 : 가장 가까운 세 사람의 심리적 거리 (C++)

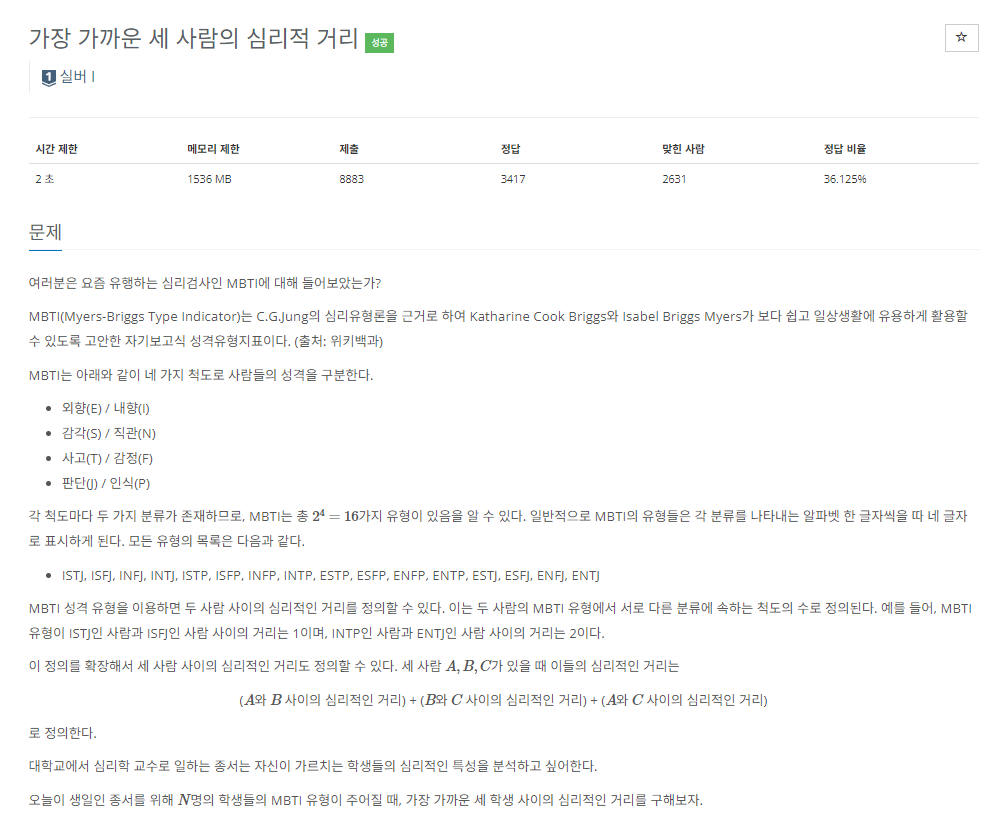
풀이 방법 : 브루트포스 , 비둘기 집 원리

완전탐색의 냄새가 나긴 하지만 입력값 N의 최댓값이 100000이므로 모든 경우를 O(n^3)의 방법으로 탐색하면 무조건 시간 초과가 날 것이다.

여기서 비둘기집 원리를 사용해야 하는데 MBTI에서 가능한 모든 경우의 수는 16개이다.
따라서 만약 17명의 사람이 모이게 된다면 MBTI가 같은 사람이 적어도 두 명은 존재한다는 뜻이 될 것이다.

이와 비슷하게 만약 33명(= 16 * 2 + 1)이 모이게 된다면 MBTI가 같은 사람이 적어도 세 명은 존재하게 될 것이다. 따라서 33명 이상일 경우에는 계산을 할 필요도 없이 가장 가까운 세 사람의 심리적 거리는 무조건 0이 될 것이다.

따라서 이 문제는 테스트 케이스에서 주어지는 N이 32이하일 경우에만 완전 탐색으로 처리해주고 그를 초과하는 경우에는 무조건 0을 출력해주면 된다.

#include <iostream>
#include <vector>

using namespace std;

int CheckDist(const string& A, const string& B)
{
	int Dist = 0;

	for (int i = 0; i < 4; ++i)
	{
		if (A[i] != B[i])
			++Dist;
	}

	return Dist;
}

int main()
{
	cin.tie(nullptr);
	cout.tie(nullptr);
	ios::sync_with_stdio(false);

	int T;
	cin >> T;

	while (T > 0)
	{
		int N;
		cin >> N;

		vector<string> vecString;

		for (int i = 0; i < N; ++i)
		{
			string MBTI;
			cin >> MBTI;

			vecString.push_back(MBTI);
		}

		if (N > 16 * 2)
		{
			cout << 0 << '\n';
			--T;
			continue;
		}

		int MinDist = 16;

		for (int i = 0; i < N; ++i)
		{
			for (int j = 0; j < N; ++j)
			{
				if (i == j)
					continue;

				for (int k = 0; k < N; ++k)
				{
					if (i == k || j == k)
						continue;

					int TmpDist = 0;

					TmpDist += CheckDist(vecString[i], vecString[j]);
					TmpDist += CheckDist(vecString[j], vecString[k]);
					TmpDist += CheckDist(vecString[i], vecString[k]);

					MinDist = min(TmpDist, MinDist);
				}
			}
		}

		cout << MinDist << '\n';
		--T;
	}

}