백준 - 2568번 : 전깃줄 - 2 (C++)

풀이 방법 : LIS, 이분 탐색

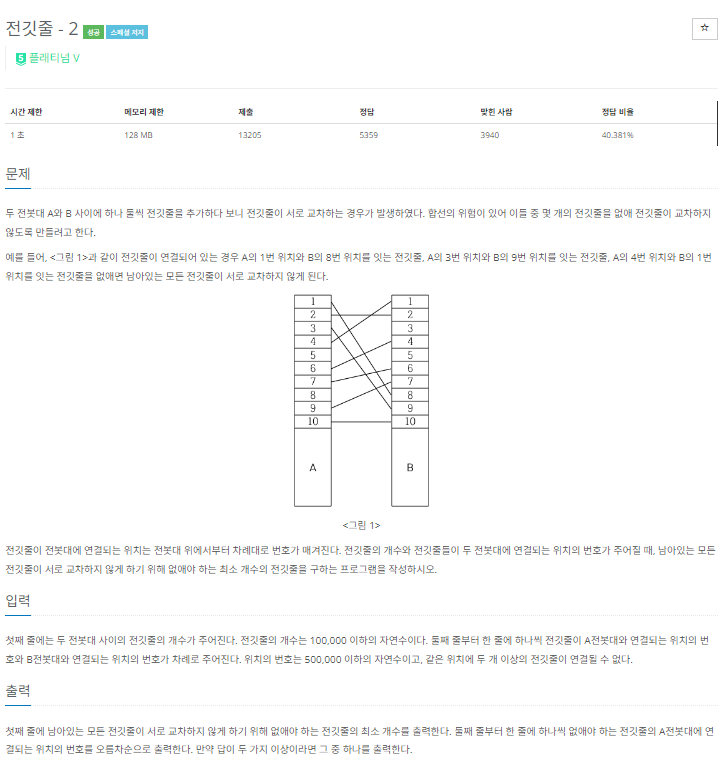
전깃줄이 어떨 때 교차가 되는지 살펴보면

왼쪽 1에서 출발한 전깃줄이 오른쪽 3에 연결되어있고, 2에서 출발한 전깃줄이 오른쪽 2에 연결된다면 그 전깃줄은 교차될 것이다. 이를 계속 생각해보면

왼쪽 숫자가 낮은 녀석의 도착지점이 왼쪽 숫자가 더 높은 전깃줄의 도착지점보다 더 높으면 교차가 된다고 생각할 수 있다.

그렇다면 왼쪽 출발지점의 숫자를 기준으로 오름차순으로 정렬한 뒤 오른쪽 숫자들의 가장 긴 증가하는 부분 수열을 구하고 그들을 제외한 전깃줄들을 오름차순으로 출력하는 것이 문제에서 요구하는 답이 된다는 것을 알 수 있다.

입력받는 전깃줄의 개수의 최대가 10만이므로 O(N^2)의 LIS 알고리즘을 사용하면 당연히 안될 것이므로 이분탐색을 이용한 O(N log N)방법을 사용해야할 것이다.

또한 어떤 요소가 부분 수열에 포함되는지를 확인할 수 있어야 하므로 부분 수열을 갱신할 때마다 삽입가능한 인덱스를 저장해주고 그를 역추적해서 부분 수열에 포함되는지 여부를 확인해줘야한다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;


int main()
{
	cin.tie(nullptr);
	cout.tie(nullptr);
	ios::sync_with_stdio(false);

	int N;
	cin >> N;

	vector<pair<int, int>> vecLine(N);

	for (int i = 0; i < N; ++i)
	{
		cin >> vecLine[i].first >> vecLine[i].second;
	}

	sort(vecLine.begin(), vecLine.end());

	vector<int> vecNum;
	vecNum.push_back(vecLine[0].second);

	vector<int> vecIdx;
	vecIdx.push_back(0);

	for (int i = 1; i < N; ++i)
	{
		int Size = vecNum.size();
		if (vecNum[Size - 1] < vecLine[i].second)
		{
			vecNum.push_back(vecLine[i].second);
			vecIdx.push_back(Size);
		}

		else
		{
			int Left = 0;
			int Right = Size - 1;

			while (Left < Right)
			{
				int Mid = (Left + Right) / 2;

				if (vecNum[Mid] < vecLine[i].second)
				{
					++Left;
				}

				else
				{
					--Right;
				}
			}

			int Mid = (Left + Right) / 2;
			vecNum[Mid] = vecLine[i].second;
			vecIdx.push_back(Left);
		}
	}

	int Size = vecNum.size();
	cout << N - (Size) << '\n';
	
	int CurIdx = vecNum.size() - 1;
	vector<int> vecAnswer;
	for (int i = vecIdx.size() - 1; i >= 0; --i)
	{
		if (CurIdx == vecIdx[i])
		{
			--CurIdx;
		}

		else
		{
			vecAnswer.push_back(vecLine[i].first);
		}
	}

	int AnsSize = vecAnswer.size();
	for (int i = AnsSize - 1; i >= 0; --i)
	{
		cout << vecAnswer[i] << '\n';
	}

}