백준 - 4485번 : 녹색 옷 입은 애가 젤다지? (C++)

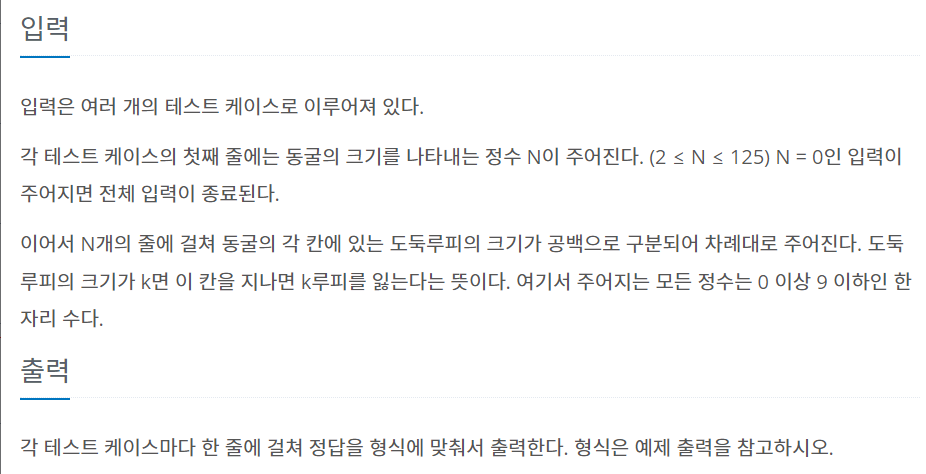
풀이 방법 : 다익스트라

처음엔 그냥 단순 다익스트라 알고리즘으로 해결하려 하였으나 만약 다른 루트에서 이미 지난 적이 있다고 하더라도, 즉 최소 이동 횟수가 아닌 루트가 최소 비용일 수 있는 경우를 고려하기 위해 DP테이블을 추가하여 해당 위치에서의 최소비용을 저장하였다.

큐를 이용한 단순 BFS로도 통과하긴 하지만 당연하게도 우선순위 큐를 사용하여 탐색을 하는 것이 현저하게 빠르다.

정답 코드 C++ , 다익스트라 풀이

#include <iostream>
#include <queue>

using namespace std;

int DirX[4] = { 0,0,1,-1 };
int DirY[4] = { 1,-1,0,0 };

struct Pos
{
	int X = 0;
	int Y = 0;
	int Cost = 0;
};

struct cmp
{
	bool operator() (const Pos& A, const Pos& B)
	{
		return A.Cost > B.Cost;
	}
};

int main()
{
	int Map[126][126] = {};
	int DP[126][126] = {};

	int CaseNum = 1;

	while (true)
	{
		int N;
		cin >> N;
		
		if (N == 0)
			break;

		for (int i = 0; i < N; ++i)
		{
			for (int j = 0; j < N; ++j)
			{
				int Rupee;
				cin >> Rupee;

				Map[i][j] = Rupee;
				DP[i][j] = -1;
			}
		}

		priority_queue<Pos, vector<Pos>, cmp> pqPos;
		Pos Start;
		Start.Cost = Map[0][0];
		DP[0][0] = Map[0][0];
		pqPos.push(Start);

		while (!pqPos.empty())
		{
			Pos CurrentPos = pqPos.top();
			pqPos.pop();

			if (CurrentPos.X == N - 1 && CurrentPos.Y == N - 1)
				break;

			for (int i = 0; i < 4; ++i)
			{
				Pos NextPos = CurrentPos;
				NextPos.X += DirX[i];
				NextPos.Y += DirY[i];

				if (NextPos.X < 0 || NextPos.X >= N
					|| NextPos.Y < 0 || NextPos.Y >= N)
					continue;

				NextPos.Cost += Map[NextPos.Y][NextPos.X];

				if (DP[NextPos.Y][NextPos.X] == -1)
					DP[NextPos.Y][NextPos.X] = NextPos.Cost;

				else
				{
					if (DP[NextPos.Y][NextPos.X] <= NextPos.Cost)
						continue;

					else
						DP[NextPos.Y][NextPos.X] = NextPos.Cost;
				}

				pqPos.push(NextPos);
			}

		}

		cout << "Problem " << CaseNum << ": " << DP[N-1][N-1] << '\n';
		++CaseNum;
	}


}

위의 것이 DP + BFS 풀이 제출 정보
아래가 다익스트라 풀이 제출 정보