[BOJ] #1914. 하노이탑 (Python)

mingguriguri·2022년 11월 5일

python recursion 백준 알고리즘

Python으로 공부하는 Algorithm

목록 보기

5/10

#1914. 하노이탑

링크: https://www.acmicpc.net/problem/1914
유형: 스택/큐, 재귀함수
작성일시: 2022년 11월 5일 오후 4:58

🧐문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

원판의 개수 N (1≤N≤100)
3

출력

옮긴 횟수 K
(N이 20이하인 경우, 두번째줄부터 수행과정 출력(N이 20보다 큰 경우에는 과정은 출력할 필요가 없다.)
7
1 3
1 2
3 2
1 3
2 1
2 3
1 3

🙄과정 (아이디어)

1. 막대를 옮기는 과정

1번막대에 있는 원판을 3번 막대에 옮겨야 한다.

1개의 원판일 때는 당연히 한 번만 옮기면 된다.
n개일 때는 어떻게 될까?

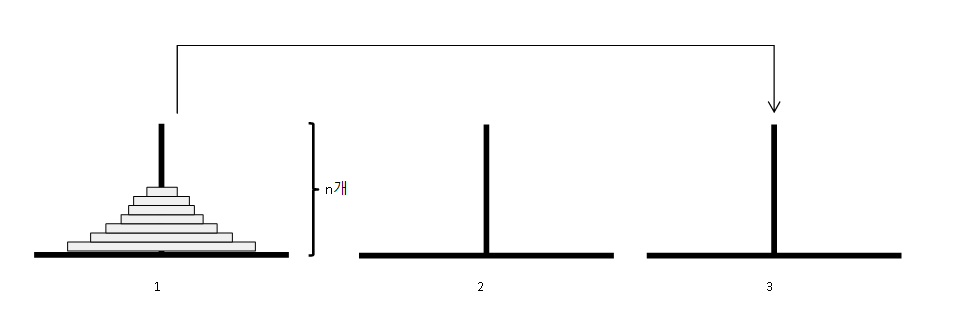
총 3단계로 나뉜다! (옮겨진 원판: 노란색)

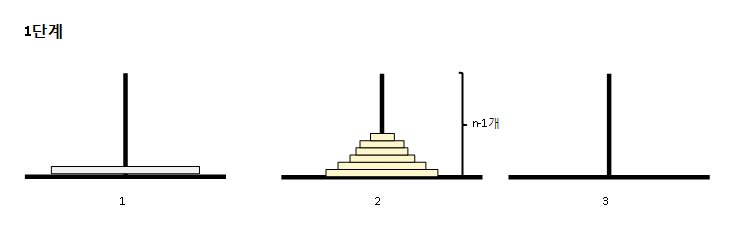
📌 1단계
n-1개의 원판을 1번막대에서 2번막대로 옮긴다.

그런데 여기서 의문점이 발생한다.

저렇게 옮기는 경우가 최소인것일까?
어떻게 옮기는 것일까?

1번 질문의 경우, 하노이탑을 잘 알고 계시다면 잘 이해할 수 있는 부분이지만 그게 아니라면 아래 영상을 2분 54초부터 보면 된다.

https://www.youtube.com/watch?v=fffbT41IuB4

2번 질문 : 재귀 알고리즘을 사용하면 쉽게 해결할 수 있다! 따라서 이 문제는 재귀함수를 이용하여 푸는 문제라고 볼 수 있다.

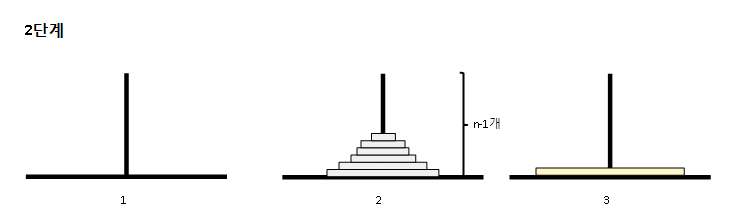
📌 2단계
남은 1개(마지막) 원판을 1번 막대에서 3번 막대로 옮긴다.

📌 3단계
다시 n-1개의 원판을 2번 막대에서 3번 막대로 옮긴다.

이 1, 2, 3단계가 핵심 아이디어이다!

그림 및 내용 출처 : https://study-all-night.tistory.com/6

2. 이동횟수

여기서 끝이 아니다!

이동횟수를 구하는 과정도 한번 살펴보자.

count를 사용해도 되는데 뒤에서 안 되는 이유를 자세히 살펴보겠다. 지금은 나열을 해보며 규칙성을 먼저 찾아보자

N이 원판개수일 때, 이동횟수

N = 1 → 1
N = 2 → 3
N = 3 → 7
N = 4 → 15
N = 5 → 31

1열로 나열해보면 1, 3, 7, 15, 31…이 된다.

이를 통해 $2^{n-1}+1$ 임을 확인할 수 있다. 이 식은 이동횟수를 출력할 때 활용하면 된다.

💡결과(풀이)

편한 이해를 위해 다른 분의 코드(다른코드#1)를 먼저 소개하고자 한다.

(위의 과정 설명부분의 아이디어를 참고한 블로그의 풀이이다.)

이후 내 코드를 소개해 어떤 점이 실패했는지 분석하고, 내 코드 방식과 유사한 다른 분의 코드(다른코드#2)도 참고로 가져왔다. 차이점이 있다면 재귀함수에서 호출하는 파라미터 개수가 다르다는 것이다.

✔다른 코드 #1

출처 : https://study-all-night.tistory.com/6

아래 코드는 하노이탑 그림과 함께 이해가 잘 되도록 아이디어 설명을 해주신 study-all-night님의 코드이다.

코드 설명은 study-all-night님의 설명에 일부 추가했다.

def hanoi_tower(n, start, end) :
    if n == 1 :
        print(start, end)
        return

    hanoi_tower(n-1, start, 6-start-end) # 1단계
    print(start, end) # 2단계
    hanoi_tower(n-1, 6-start-end, end) # 3단계

n = int(input())
print(2**n-1)
hanoi_tower(n, 1, 3)

세부적으로 코드를 보자.

함수선언

# 재귀함수 선언
def hanoi_tower(n, start, end)
# n : 원판 개수
# start, end : n개의 원판을 ' 몇 번 막대에서 몇 번 막대로 옮길거야'의 데이터를 담은 변수

함수 내용 #1. 재귀호출

    hanoi_tower(n-1, start, 6-start-end) # 1단계
    print(start, end) # 2단계
    hanoi_tower(n-1, 6-start-end, end) # 3단계

📌1단계

start막대(1번 막대)에 있는 n개의 원판 중 n-1개의 원판을 end막대(3번 막대)가 아닌 2번 막대로 옮긴다.

이때 start와 end는 번호를 알지만 나머지 막대의 번호를 알지 못한다.

⇒ 하지만 start, end막대와, 중간 막대를 다 합치면 6이 된다!(1+2+3)

따라서 2번 막대로 옮기는 식은 6-start-end 이다.

📌2단계

그림처럼 start막대에서 end막대로 옮겨주면 된다.

📌3단계

1단계와 같은 메커니즘으로 작동한다. 2번 막대에 있던 n-1개의 원판을 end막대(3번 막대)로 옮겨준다.

또한 이때, n-1을 해주어 원판의 개수도 줄여줘야 한다.

함수내용 #2. 종료조건

    if n == 1 :
        print(start, end)
        return

재귀함수의 경우 종료조건이 꼭 있어야 한다. 종료조건이 있지 않다면, 무한으로 빠질 가능성이 있기 때문이다.

원판(n)이 마지막 1개 남았을 때, 1번막대에서 3번막대로 옮기면서 종료가 되고, 이는 모든 경우가 다 동일하게 1→3이기 때문에 print문으로 출력하고 return 해준다.

메인

n = int(input())
print(2**n-1) #이동횟수
hanoi_tower(n, 1, 3)

메인함수 부분은 입력부분, 이동횟수 출력, hanoi_tower함수를 호출해 과정 출력한다.

코드 보완

이 코드는 정말 잘 짰지만! 그래도 추가하면 좋을 점을 얘기해보자면,

❗ 문제 조건에서 n이 20개 이하일 경우는 과정을 출력하고, 20개 초과가 되면 과정을 출력하지 않는다고 했는데, 이 부분은 고려하지 않은 것 같다!

따라서 이 부분을 추가하여 보완한 코드는 다음과 같다.

def hanoi_tower(n, start, end) :
    if n == 1 :
        print(start, end)
        return
     
    hanoi_tower(n-1, start, 6-start-end) # 1단계
    print(start, end) # 2단계
    hanoi_tower(n-1, 6-start-end, end) # 3단계

n = int(input())
print(2**n-1)
#여기 if부분
if n <= 20 :
    hanoi_tower(n, 1, 3)

✔내 코드

나는 풀다가 내 코드에 막혀서 내가 recrusive되어서 마지막에 엄청 헷갈렸다. 그래서 코드를 제대로 보지 못했던 것 같다.

따라서 다른 사람의 아이디어와 풀이과정을 통해 다시 이해하는 과정을 거쳤다. (그래서 위 코드와 아래 코드 첨부)

우선 내가 한 풀이는 다음과 같다.

N = int(input())
count = 0 #옮긴 횟수 K
def hanoi(one, two, three, N):
  global count
  if N == 1:
    print(one, three)
    return

  if N < 20:
    count += 1
    print(one, three)
    hanoi(two, one, three, N-1)
    hanoi(one, three, two, N-1)

print(count)
hanoi(1,2,3,N) #하노이함수 호출

하지만 다음과 같은 에러가 났다.

File "<ipython-input-18-7d2b3049cc22>", line 8
    hanoi(one, three, two, N-1)
                               ^
TabError: inconsistent use of tabs and spaces in indentation

코드 실패 원인분석

내가 짜놓고도 이해할 수 없는 코드

내 풀이지만 중간에 친구의 힌트를 듣고 내 풀이와 맞지 않게 마구잡이로 코드를 집어넣게 되었다. 결과적으로 코드를 풀다가 자꾸 미로로 빠지게 되었다…
이동횟수를 위해 count변수를 사용했지만, 사실상 정답이 될 수가 없다. 출력화면 첫줄에 이동횟수가 나와야지만, count를 사용한다면 마지막줄에 출력해야 한다.

⇒ 그래서 다른 사람들이 이 공식을 사용한 것 같다.
이런 공식은 미리 알고 있으면 좋겠지만, 직접 나열해보고 규칙을 찾아가는 식으로 해도 풀 수 있다.

내 코드를 어떻게 보완할 수 있을까? 하다가 유사한 코드를 발견하였다. 아래에서 소개하겠다.

✔다른 코드 #2

출처 : https://justicehui.github.io/ps/2019/05/06/BOJ1914/

def f(n, a, b, c):
  if(n == 1):
    print(a, c, sep = " ")
  else:
    f(n-1, a, c, b) #1단계
    f(1, a, b, c) #2단계
    f(n-1, b, a, c) #3단계

n = int(input()) #입력
print(2**n-1) #이동횟수 출력
if(n <= 20): #함수 조건
  f(n, 1, 2, 3) #함수 호출

코드에 대한 자세한 분석은 위에서 했기 때문에 생략하겠다!

✔내 코드 보완

위의 다른 분들의 코드(다른코드#1, 다른코드#2)를 통해 내 코드를 다시 보완해보았다.

#하노이 함수
def hanoi(one, three, N):
    if N == 1:
        print(one,three)
        return
   
    hanoi(one, 6-one-three, N-1) #1단계 (1->2)
    print(one, three) #2단계 (마지막원반 1->3)
    hanoi(6-one-three, three, N-1) #3단계 (2->3)

#메인
N = int(input())
print(2**n-1)
if N <= 20:
    hanoi(1,3,N)

근데 이렇게 하니까 런타임에러가 났다. 에러는 NameError

그래서 정말 찐 최종 코드

#하노이 함수
def hanoi_f(one, three, n):
    if n == 1:
        print(one,three)
        return

    hanoi_f(one, 6-one-three, n-1) #1단계 (1->2)
    print(one, three) #2단계 (마지막원반 1->3)
    hanoi_f(6-one-three, three, n-1) #3단계 (2->3)

#메인
n = int(input())
print(2**n-1)
if n <= 20:
    hanoi_f(1,3,n)