O(N²) 정렬 알고리즘 속도 비교 : 버블, 선택, 삽입

미키오·2024년 8월 14일

0. 들어가며

코딩테스트나 사이드 프로젝트와 같이 프로그래밍을 하다 보면, 데이터를 효율적으로 정리하고 처리하는 것이 중요함을 점점 뼈저리게 느끼게 된다.
특히 알고리즘을 공부하면서 프로그래머스나 코드트리에 답변을 저장 후 제출하면 시간 초과와 같은 문제를 종종 마주하게 된다. ~~인터프리터 언어탓~~ 이러한 문제를 마주할 때마다 시간 복잡도에 대한 기본적인 이해가 부족함을 깨닫게 된다.

또한 어떤 상황에서 어떤 정렬 방법이 유리하거나 불리한지 파악하는 것이 실전에서도 중요하다. 이번 글에서는 JavaScript를 사용하여 공통적으로 O(N²)의 시간 복잡도를 가지는 거품 정렬(Bubble Sort), 선택 정렬(Selection Sort), 삽입 정렬(Insertion Sort)을 직접 구현하고, 다양한 테스트 케이스를 통해 실험을 진행해 보았다. 이를 통해 각 알고리즘의 수행 시간이 왜 다르게 나오며, 특정 상황에서 어떤 알고리즘이 더 유리한지에 대해 탐구해 보겠다.

1. 거품정렬 Bubble Sort

거품 정렬은 기본적인 아이디어부터가 매우 간단하다.

첫번째 값과 두번째 값을 비교하고, 이어서 두번째 값과 세번째 값을 비교하고,
세번째 값과 네번째 값을 비교하고 … n-1번째와 n번째 값을 비교하며 이 과정에서
순서가 맞지 않은 값은 서로 교환해준다.
이런 절차를 정렬이 될 때까지 반복한다.

여기에선 37을 제외하고 동일한 교환 과정을 반복하면 된다.

function bubbleSort(arr) {
    let n = arr.length;
    let swapped;
    do {
        swapped = false;
        for (let i = 0; i < n - 1; i++) {
            if (arr[i] > arr[i + 1]) {
                let temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
                swapped = true;
            }
        }
        n--;
    } while (swapped);
    return arr;
}

하지만 교환 여부를 확인하기 위해 전체 값을 한 바퀴 돌아야하므로 상당히 비효율적이고 성능도 다른 알고리즘에 비해 떨어진다.

최악의 경우, 각 원소가 정렬될 최종 위치에 도달하기 전까지 반복적으로 비교 및 교환이 일어나야 하므로, 시간 복잡도는 N(N-1)/2 비교와 교환으로 O(N²)이 된다.

2. 선택정렬 Selection Sort

가장 일상적인 방법이라 평가받는 알고리즘이다.

우선 선택 정렬에서는 전체 값 중에서 가장 작은 값을 찾아야 한다.

그 후 해당 값을 가장 맨 앞에 배치한다. (arr[0]) 기존에 맨앞에 있던 숫자는 최솟값이 있었던 자리로 옮겨준다.

다음 차수에서는 첫번째 값을 제외하고 가장 작은 값을 찾아 두번째에 배치한다. (arr[1])

두번째, 세번째, … n-1번째 값을 제외하고 가장 작은 값을 찾아 정해진 위치에 배치하는 것을 반복한다.

function selectionSort(arr) {
	let n = arr.length;
	for (let i = 0; i < n-1; i++) {
    let min = i;
    for (let j = i+1; j < n; j++) {
        if (arr[j] < arr[min]) {
            min = j
        }
    }
    let tmp = arr[i]
    arr[i] = arr[min]
    arr[min] = tmp
	}
	return arr;
}

선택 정렬의 경우 반드시 n-1, n-2, … ,2,1 번의 비교 연산을 수행해야 한다. 즉, n * (n-1)/2 번의 연산을 필요로 한다. 이는 중간에 정렬된 상태라면 종료될 수 있는 거품 정렬과는 구분된다.

그러므로 시간복잡도는 O(N²)이 된다.

3. 삽입정렬 Insertion Sort

삽입 정렬은 앞에서부터 순차적으로 보면서 상단에 있는 모든 원소가 정렬이 되어있다는 가정 하에 현재 원소의 위치를 삽입하는 정렬이다.

즉, 원소가 1개인 경우부터, 2번째 원소, 3번째 원소, ... n번째 원소까지 진행하며 앞의 원소들을 전부 오름차순을 유지하며 진행하는 방법이다.

예를 들어, 다음 사진과 같이 3번째 원소까지 정렬이 진행되었을 경우([1,11,14]), 4번째 원소를 진행해본다고 가정을 해보자. 이때 삽입 정렬은, 앞 원소들은 (1~3번째까지) 정렬이 되어있는 상황이고, 이제 숫자 7을 적절한 위치에 넣어서 4개의 원소가 모두 오름차순 정렬이 되도록 만들려고 한다.

가장 먼저 현재 위치에 있던 7을 앞에 있는 원소 (여기서는 14) 와 비교하여 현재 위치의 7이 더 작다면 두 원소의 위치를 바꿔준다.

swipe가 일어난 후에도 앞에 원소(여기서는 11)과 비교 했을때 앞에 있는 원소가 더 크다면 두 원소의 위치를 또다시 바꿔준다.

앞에 있는 원소가 더 커지지 않는 경우에 도달한다면, 멈춘다.

function insertionSort(arr) {
	let n = arr.length;
	for (let i = 1; i < n; i++) {
    let key = arr[i];
    j = i - 1;
    while (j >= 0 && arr[j] > key) {
        arr[j+1] = arr[j]
        arr[j] = key;
        j--;
    }
    arr[j+1] = key;
	}
	return arr;
}

삽입 정렬의 경우, n개의 원소에 대해 값 삽입을 수행할때 2번째 원소의 경우엔 최대 1개의 원소를 이동, 3번째 원소의 경우엔 최대 2개의 원소를 이동 … n번째 원소까지 삽입하는 경우엔 최대 n-1개의 원소가 이동해야 하므로 결과적으로 최대 n(n-1)/2개의 원소가 이동해야 한다.

따라서 이 역시 버블, 선택과 동일하게 O(N²)의 시간 복잡도가 나온다.

정렬 속도 비교

앞서 살펴본 거품, 선택, 삽입 정렬 알고리즘 시간복잡도는 O(N^2)라는 공통점이 있지만, 동작되는 원리를 살펴보면 실제 소요되는 시간은 많이 다르다는 것을 예상할 수 있다.

따라서 해당 실험은 거품 정렬(Bubble Sort), 선택 정렬(Selection Sort), 그리고 삽입 정렬(Insertion Sort)의 성능을 비교하여 각 알고리즘의 시간 복잡도 O(N^2) 가 실제로 다양한 데이터 배열 상태에서 어떻게 다르게 작동하는지를 평가하기 위함이다.

실험 환경

플랫폼: Visual Studio Code (VSCode)
실행 환경: Node.js
측정 도구: console.time과 console.timeEnd를 사용하여 각 정렬 알고리즘이 배열을 정렬하는 데 소요된 시간을 밀리초 단위로 측정했다.
- console.time(label): 특정 코드 실행 시간 측정을 시작한다. label은 해당 타이머의 이름을 지정한다.
- console.timeEnd(label): console.time으로 시작된 타이머를 멈추고, 시작점부터 종료점까지의 시간을 콘솔에 출력한다. 출력된 시간은 label과 함께 나타나므로, 여러 타이머를 구분할 수 있다.

실험 조건 및 데이터

실험에 사용된 입력 데이터는 다음과 같다:

이미 정렬된 배열: [1, 2, 3, 4, 5, 6, 7]
역순으로 정렬된 배열: [7, 6, 5, 4, 3, 2, 1]
요소가 전부 같은 배열: [1, 1, 1, 1, 1, 1, 1, 1]
랜덤 배열: [23, 15, 38, 94, 62, 123, 243, 234, 112]

실험 절차

각 정렬 알고리즘에 대해 위의 네 가지 유형의 배열을 입력으로 제공하고, 각각에 대해 정렬을 수행할 때의 시작 시간과 종료 시간을 측정하여 정렬 소요 시간을 기록하다. 이를 통해 각 정렬 방식의 효율성을 평가하고, 특정 상황에서의 장단점을 분석하였다.

거품 정렬

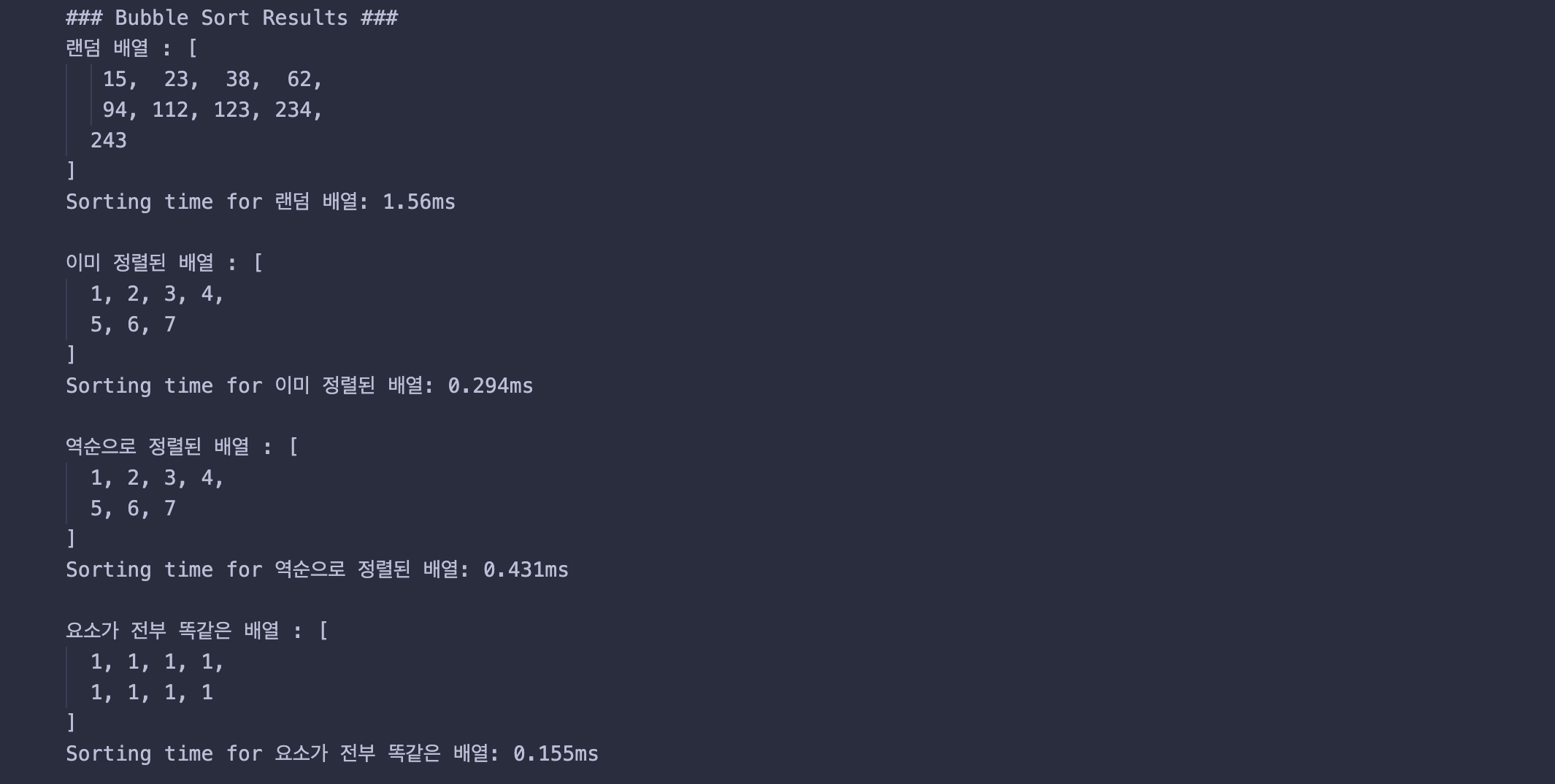
랜덤 배열: 실행 시간 1.56ms. 배열의 무작위 정렬 상태에서는 많은 비교와 교환 작업이 필요하므로 시간이 많이 소요된다.
이미 정렬된 배열: 실행 시간 0.294ms. 배열이 이미 정렬되어 있으면, 거의 어떠한 교환도 일어나지 않으므로 처리 시간이 크게 줄어든다.
역순으로 정렬된 배열: 실행 시간 0.431ms. 역순 배열에서는 최악의 경우가 발생하여 많은 교환이 필요하지만, 여전히 빠른 처리가 가능하다.
요소가 전부 같은 배열: 실행 시간 0.155ms. 모든 요소가 동일하면 교환이 필요 없으므로 가장 빠르다.

성능에 영향을 미치는 요소:

비교 횟수:
- 거품 정렬은 매 반복마다 인접한 원소들을 전체적으로 비교하기 때문에 비교 횟수가 많다. 이는 특히 배열이 무작위로 섞여 있을 때 더욱 두드러진다. 모든 원소가 최악의 위치에 있을 경우(예: 역순), 모든 가능한 위치 교환이 이루어져야 하기 때문이다.
교환 횟수:
- 교환은 물리적으로 두 원소의 위치를 바꾸는 것을 포함하기 때문에 시간 소모적이다. 무작위 배열에서는 거의 모든 비교가 교환으로 이어질 수 있다.

왜 정렬된 배열에서는 빠른가?

정렬된 배열에서 거품 정렬은 다른 배열에 비해 매우 빠르게 작동한다. 이는 배열을 한 번 스캔하는 동안 어떤 교환도 일어나지 않기 때문이다. 거품 정렬 알고리즘은 교환이 한 번도 일어나지 않으면 정렬이 완료되었다고 판단하고 조기 종료할 수 있기 때문에, 이미 정렬된 배열에서는 최적의 경우 O(N)의 시간 복잡도를 가진다.

왜 요소가 전부 같은 배열에서는 빠른가?

요소가 전부 같은 배열 역시 정렬된 배열과 유사한 이유로 빠르게 처리된다. 모든 원소가 같기 때문에 교환이 필요 없다. 따라서 거품 정렬은 첫 번째 스캔에서 아무런 교환이 이루어지지 않아 바로 정렬이 완료된 것으로 인식하고 처리를 종료한다.

선택 정렬

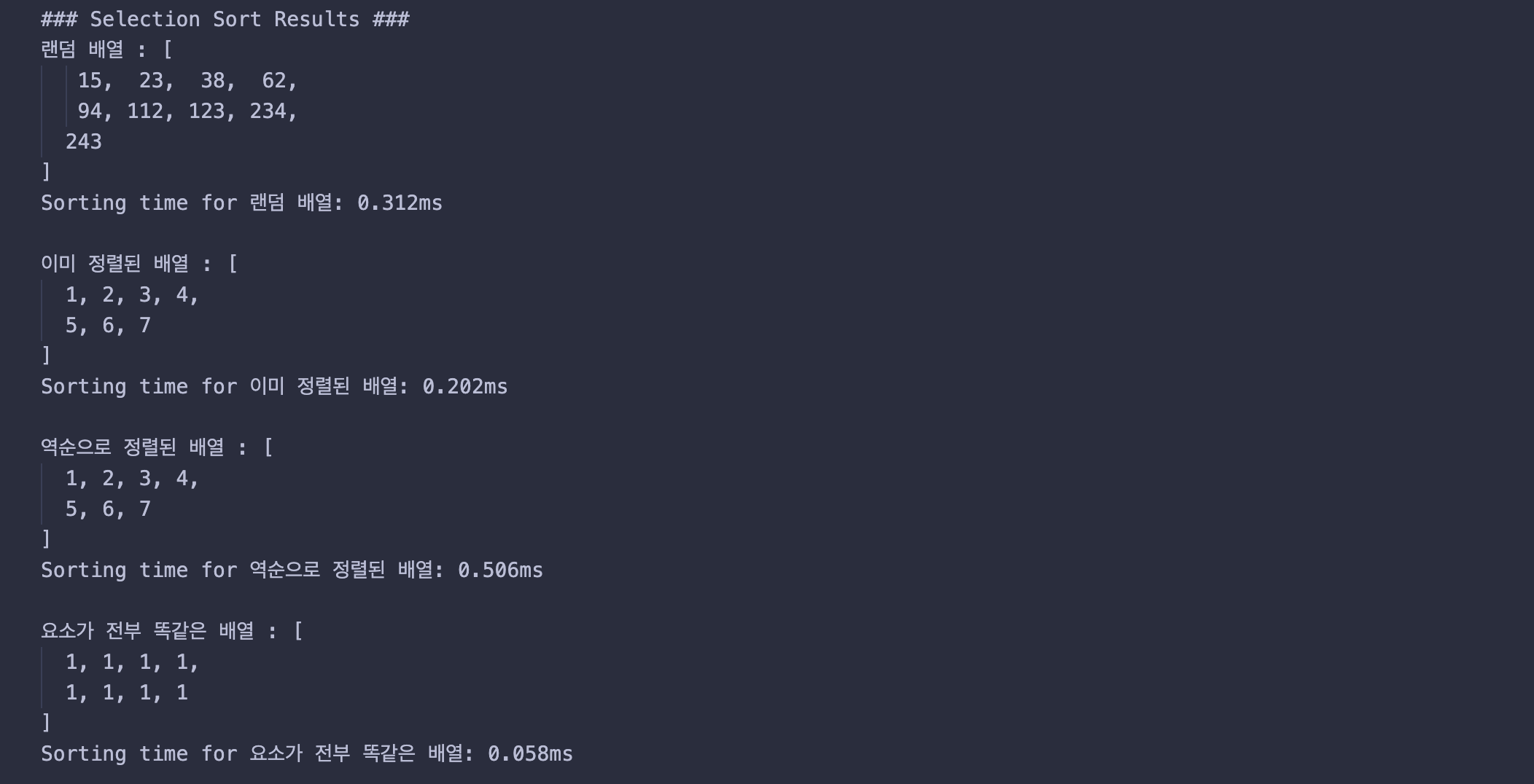
선택 정렬은 매 단계에서 전체 배열을 순회하여 현재 위치에 들어갈 최소 값을 찾고, 그 값을 현재 위치로 이동시키는 방식으로 작동한다. 이러한 특징 때문에, 배열의 초기 상태와는 상대적으로 독립적인 성능을 보였다.

랜덤 배열: 실행 시간 0.312ms. 배열 상태와 무관하게 일정한 비교 횟수가 필요.
이미 정렬된 배열: 실행 시간 0.202ms. 최소 검색이 간단하므로 약간 더 빠르다.
역순으로 정렬된 배열: 실행 시간 0.506ms. 각 단계에서 최소값을 찾기 위한 비교가 상대적으로 많이 필요.
요소가 전부 같은 배열: 실행 시간 0.058ms. 모든 값이 같기 때문에 비교는 역시나 빠르고 간단하다.

성능에 영향을 미치는 요소

비교 횟수:
- 선택 정렬은 배열의 각 위치에 대해 나머지 부분과 비교를 수행하여 최소값을 찾는다. 따라서 N−1,N−2,…,1번의 비교를 수행하므로 총 비교 횟수는 2N(N−1)로, 입력 배열의 상태에 상관없이 일정하다.
교환 횟수:
- 선택 정렬은 최소값을 찾은 후에만 위치를 교환하기 때문에 교환 횟수는 N−1번으로 고정되어 있다. 다시말해, 이는 배열의 상태에 관계없이 일정한 수의 교환이 이루어진다는 것을 의미한다.

왜 랜덤 배열과 역순 배열에서 성능 차이가 나는가?

랜덤 배열: 선택 정렬은 비교가 고르게 분포되어 있으므로 랜덤 배열에서도 일정한 성능을 유지한다.
역순 배열: 각 단계에서 최소값을 찾기 위한 비교는 동일하나, 배열의 상태에 따른 성능 영향은 미미하며, 주로 최악의 경우라고 할 수 있는 역순 배열에서도 다른 알고리즘에 비해 안정적인 성능을 보여준다.

삽입 정렬 (Insertion Sort)

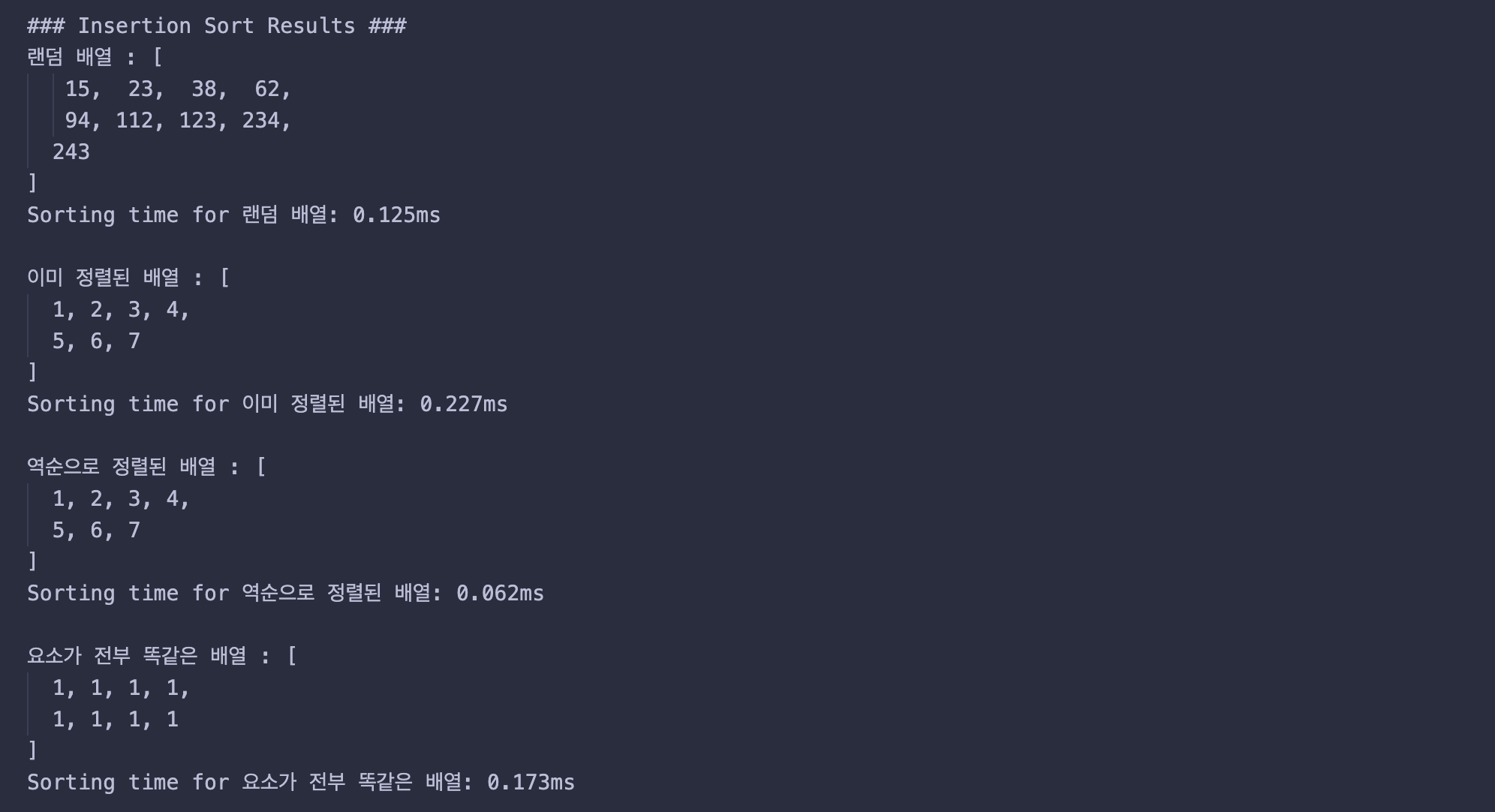
삽입 정렬은 각 반복에서 원소를 적절한 위치에 삽입하는 방식으로 정렬을 진행한다. 실험 결과는 다음과 같다:

랜덤 배열: 실행 시간 0.125ms. 중간 수준의 비교와 교환 작업이 필요하다.
이미 정렬된 배열: 실행 시간 0.227ms. 원소가 이미 적절한 위치에 있어 빠른 처리가 가능하다.
역순으로 정렬된 배열: 실행 시간 0.062ms. 각 원소가 최소값이 되어 삽입 위치를 찾는 것이 간단하다.
요소가 전부 같은 배열: 실행 시간 0.173ms. 비교가 적고 간단하여 빠른 정렬이 가능하다.

성능에 영향을 미치는 요소

비교 횟수:
- 각 원소는 이전의 모든 원소와 비교될 수 있으므로 최악의 경우 비교 횟수는 N(N-1)/2이다. 이는 배열이 역순으로 정렬되어 있을 때 발생한다.
교환 횟수:
- 각 비교에서 원소가 이전 위치보다 작다면, 원소는 삽입될 위치까지 이동해야 하므로 이동(교환) 횟수는 비교 횟수와 거의 동일할 수 있다.

왜 역순 배열에서는 성능이 나빠지는가?

역순 배열: 각 원소가 최소값이 되어 배열의 맨 앞까지 이동해야 하므로 많은 이동이 필요하다. 삽입 정렬은 이미 부분적으로 정렬된 배열에서는 매우 빠르게 작동하지만, 역순 배열에서는 각 원소가 매번 맨 앞으로 이동해야 하므로 많은 연산이 필요하다.

왜 이미 정렬된 배열에서는 빠른가?

이미 정렬된 배열: 이미 정렬된 배열에서는 각 원소가 이미 적절한 위치에 있기 때문에 추가적인 이동이 거의 또는 전혀 필요하지 않다. 이로 인해 삽입 정렬은 정렬된 배열에서 매우 빠르게 작동하며, 이 경우 시간 복잡도는 O(N)으로 최적화된다.

결론

통상적으로 거품 정렬이 셋 중에서는 가장 느리지만 정렬된 배열의 경우, sorted의 값이 계속 true이기 때문에(swipe를 할 필요 x) 시간이 엄청 빨라진다.

선택 정렬의 경우에는 배열의 상태와 상관 없이, 1번째로 작은 원소를 찾고, 2번째로 작은 원소를 찾고, 3번째로 작은 원소를 찾고, … 하는 과정을 거치기 때문에 배열이 중구난방이던 정렬된 상태던 동일한, 일관적인 시간을 보여준다.

삽입 정렬의 경우에는 셋 중에서는 가장 빠르나, 값이 역순으로 정렬되어 있는 경우 성능이 많이 떨어진다는 단점이 있다는 것을 알 수 있었다.

그러나 앞 배열에 값을 삽입하는 삽입 정렬의 특성상 이미 정렬된 배열에 추가적으로 값을 몇개 추가하여 정렬하는 경우에는 좋은 성능을 보여준다.

단순히 원리와 시간복잡도만 달달 외우는 것보다 직접 코드를 구현해보고 왜 그런지 테스트 케이스를 넣어보며 실험을 해보니 더 좋았다.

참고 : sortTest 구현 전체 코드

function bubbleSort(arr) {
  let n = arr.length;
  let swapped;
  do {
    swapped = false;
    for (let i = 0; i < n - 1; i++) {
      if (arr[i] > arr[i + 1]) {
        let temp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = temp;
        swapped = true;
      }
    }
    n--;
  } while (swapped);
  return arr;
}

function selectionSort(arr) {
  let n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    let min = i;
    for (let j = i + 1; j < n; j++) {
      if (arr[j] < arr[min]) {
        min = j;
      }
    }
    let tmp = arr[i];
    arr[i] = arr[min];
    arr[min] = tmp;
  }
  return arr;
}

function insertionSort(arr) {
  let n = arr.length;
  for (let i = 1; i < n; i++) {
    let key = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      arr[j] = key;
      j--;
    }
    arr[j + 1] = key;
  }
  return arr;
}

function testSorting(sortFunction, arr, description) {
  console.time(`Sorting time for ${description}`);
  console.log(description, ":", sortFunction([...arr])); // 배열을 복사하여 원본 데이터 유지
  console.timeEnd(`Sorting time for ${description}`);
}

const arr = [23, 15, 38, 94, 62, 123, 243, 234, 112];
const arr1 = [1, 2, 3, 4, 5, 6, 7];
const arr2 = [7, 6, 5, 4, 3, 2, 1];
const arr3 = [1, 1, 1, 1, 1, 1, 1, 1];

console.log("### Bubble Sort Results ###");
testSorting(bubbleSort, arr, "랜덤 배열");
console.log();
testSorting(bubbleSort, arr1, "이미 정렬된 배열");
console.log();
testSorting(bubbleSort, arr2, "역순으로 정렬된 배열");
console.log();
testSorting(bubbleSort, arr3, "요소가 전부 똑같은 배열");
console.log();

console.log("\n### Selection Sort Results ###");
testSorting(selectionSort, arr, "랜덤 배열");
console.log();
testSorting(selectionSort, arr1, "이미 정렬된 배열");
console.log();
testSorting(selectionSort, arr2, "역순으로 정렬된 배열");
console.log();
testSorting(selectionSort, arr3, "요소가 전부 똑같은 배열");
console.log();

console.log("\n### Insertion Sort Results ###");
testSorting(insertionSort, arr, "랜덤 배열");
console.log();
testSorting(insertionSort, arr1, "이미 정렬된 배열");
console.log();
testSorting(insertionSort, arr2, "역순으로 정렬된 배열");
console.log();
testSorting(insertionSort, arr3, "요소가 전부 똑같은 배열");
console.log();

📚Bibliography

geek for geeks bubble sort, insertion sort, select sort
https://www.geeksforgeeks.org/bubble-sort-algorithms-by-using-javascript/
mdn console.time https://developer.mozilla.org/ko/docs/Web/API/console/time_static
코드트리 알고리즘 입문
https://www.codetree.ai/curriculums/2

미키오

교육 전공 개발자 💻

이전 포스트

데이터베이스 용어정리

다음 포스트

O(N²) 정렬 알고리즘 속도 비교 : 버블, 선택, 삽입

0. 들어가며

1. 거품정렬 Bubble Sort

2. 선택정렬 Selection Sort

3. 삽입정렬 Insertion Sort

정렬 속도 비교

실험 환경

실험 조건 및 데이터

실험 절차

거품 정렬

성능에 영향을 미치는 요소:

왜 정렬된 배열에서는 빠른가?

왜 요소가 전부 같은 배열에서는 빠른가?

선택 정렬

성능에 영향을 미치는 요소

왜 랜덤 배열과 역순 배열에서 성능 차이가 나는가?

삽입 정렬 (Insertion Sort)

성능에 영향을 미치는 요소

왜 역순 배열에서는 성능이 나빠지는가?

왜 이미 정렬된 배열에서는 빠른가?

결론

참고 : sortTest 구현 전체 코드

📚Bibliography

데이터베이스 용어정리

웹 페이지가 로드되기까지 : www.google.com의 여정

0개의 댓글