푸리에 급수를 유도해보자

milkbottle·2024년 5월 22일
0

푸리에 급수란

영상처리, 신호와 시스템 등 공학에서 가장 중요한 것은 푸리에 급수와 푸리에 변환이다.

많이 어려워서 이해를 하기 위해 글로 표현해서 공부해보기로 했다.

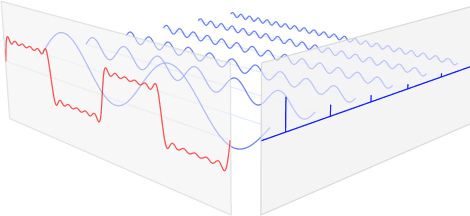
먼저 결과부터 말하자면, 빨간색의 복잡한 신호가 있다고 가정하자.

이 세상의 모든 복잡한 신호(빨간색)는 간단한 신호(파란색)의 합으로 나타낼 수 있다.

참고로 간단한 신호라 함은 코사인 함수이다.

왜 사인함수는 아니냐하면, 사인함수를 평행이동 시키면 코사인함수이기 때문이다.


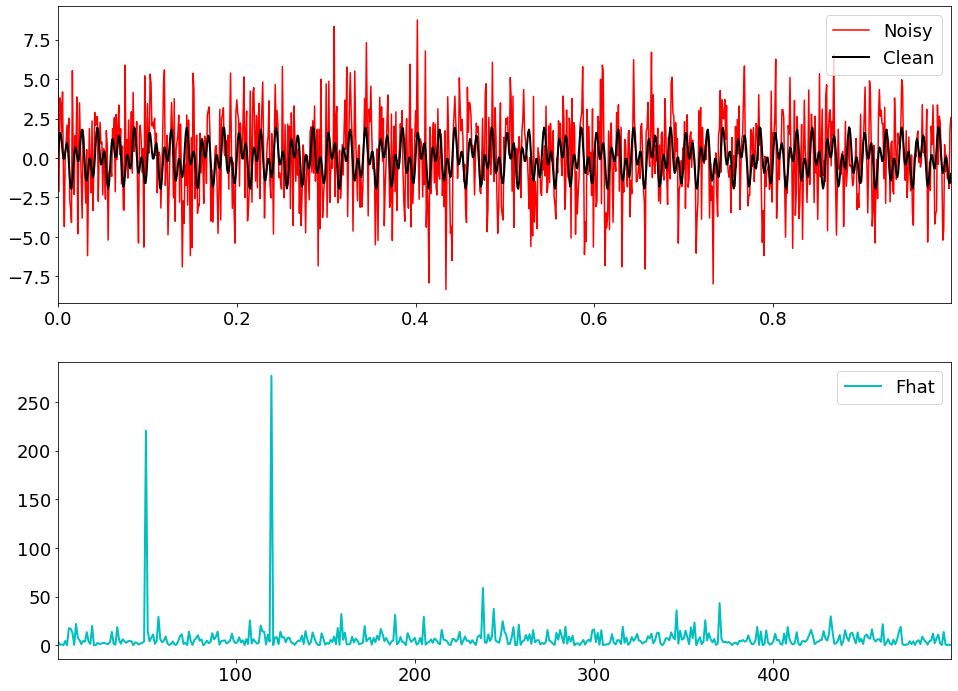
또한 빨간색의 노이즈와 검은색의 원본노이즈가 있다고 하자.

이를 푸리에 변환을 통해 청록색의 그래프로 나타낼 수 있다.

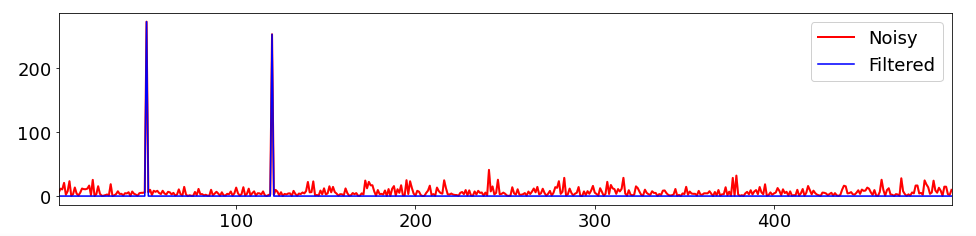
이를 구분해 잔잔바리의 노이즈를 제거하고 기존의 깔끔한 원본 신호를 가져올 수도 있다.

이래서 푸리에 변환은 노이즈 제거에 중요하다.

그래서 영상처리나 음원처리 등 각종 프로세싱 과정에서 많이 쓰인다.

푸리에 급수 유도

간단한 신호들의 합

특정 시간 tt초일 때, 복잡한 신호 f(t)f(t)에 관한 식을 삼각함수들의 합으로 표현할 수 있다.

f(t)=a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )f(t) = a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)

단순한 신호들은 정수배의 주기로 이루어져있다.

그리고 신호는 y절편처럼 편차가 존재하기 때문에 상수 a0a_0도 식에 존재한다.

이를 무한대로 활용하면 f(t)=a0+∑n=1∞(ancos⁡nωt+bnsin⁡nωt)f(t) = a_0 + \sum_{n=1}^{\infin}(a_n\cos n\omega t+b_n\sin n\omega t)이다.

여기서 a0a_0~a∞a_\infin과 b1b_1~b∞b_\infin계수들만 알면 주기함수의 합으로 신호를 표현할 수 있는 것이다.

사전에 알아야할 식

∫0Tsin⁡nωtdt=0\int_{0}^{T}\sin n\omega tdt=0

∫0Tcos⁡nωtdt=0\int_{0}^{T}\cos n\omega tdt=0

∫0Tsin⁡nωtcos⁡mωtdt=0\int_{0}^{T}\sin n\omega t \cos m\omega tdt=0

∫0Tsin⁡nωtsin⁡mωtdt=0\int_{0}^{T}\sin n\omega t \sin m\omega tdt=0

∫0Tcos⁡nωtcos⁡mωtdt=0\int_{0}^{T}\cos n\omega t \cos m\omega tdt=0

∫0Tcos⁡2nωtdt=T2\int_{0}^{T}\cos^2 n\omega tdt=\frac{T}{2}

∫0Tsin⁡2nωtdt=T2\int_{0}^{T}\sin^2 n\omega tdt=\frac{T}{2}

이 식은 직접 계산해봐도 알 수 있다.

a0a_0구하기

f(t)=a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )f(t) = a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)

위 식을 적분하면 다음과 같다. 적분은 0부터 주기TT까지 시간축으로 진행한다.

∫0Tf(t)dt=∫0T[a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )]dt=∫0Ta0dt+a1∫0Tcos⁡ωtdt+a2∫0Tcos⁡2ωtdt+⋯+b1∫0Tsin⁡ωtdt+b2∫0Tsin⁡2ωtdt+…\int_{0}^{T}f(t)dt = \int_{0}^{T}[a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)]dt \\=\int_{0}^{T}a_0dt+a_1\int_{0}^{T}\cos \omega tdt+a_2\int_{0}^{T}\cos 2\omega tdt + \dots + b_1\int_{0}^{T}\sin \omega tdt+b_2\int_{0}^{T}\sin 2\omega tdt+\dots

여기서 ∫0Tsin⁡nωtdt=0\int_{0}^{T}\sin n\omega tdt=0, ∫0Tcos⁡nωtdt=0\int_{0}^{T}\cos n\omega tdt=0이기 때문에, ∫0Ta0dt\int_{0}^{T}a_0dt만 살아남는다.

즉, ∫0Tf(t)dt=∫0Ta0dt=Ta0\int_{0}^{T}f(t)dt=\int_{0}^{T}a_0dt=Ta_0이므로 a0=1T∫0Tf(t)dta_0=\frac{1}{T}\int_{0}^{T}f(t)dt

a1a_1~a∞a_\infin구하기

f(t)=a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )f(t) = a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)

이번엔 양변에 cos⁡nωt\cos n\omega t를 곱한 후 적분한다.

∫0Tf(t)cos⁡nωtdt=∫0T[a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )]cos⁡nωtdt=∫0Ta0cos⁡nωtdt+a1∫0Tcos⁡ωtcos⁡nωtdt+a2∫0Tcos⁡2ωtcos⁡nωtdt+⋯+b1∫0Tsin⁡ωtcos⁡nωtdt+b2∫0Tsin⁡2ωtcos⁡nωtdt+…\int_{0}^{T}f(t)\cos n\omega tdt = \int_{0}^{T}[a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)]\cos n\omega tdt\\=\int_{0}^{T}a_0\cos n\omega tdt+a_1\int_{0}^{T}\cos \omega t\cos n\omega tdt+a_2\int_{0}^{T}\cos 2\omega t\cos n\omega tdt + \dots + b_1\int_{0}^{T}\sin \omega t\cos n\omega tdt+b_2\int_{0}^{T}\sin 2\omega t\cos n\omega tdt+\dots

여기서 ∫0Tsin⁡mωcos⁡nωtdt=0\int_{0}^{T}\sin m\omega \cos n\omega tdt=0, ∫0Tcos⁡mωcos⁡nωtdt=0\int_{0}^{T}\cos m\omega \cos n\omega tdt=0, ∫0Tcos⁡nωtdt=0\int_{0}^{T} \cos n\omega tdt=0이기 때문에, ∫0Tancos⁡2nωtdt\int_{0}^{T}a_n\cos^2 n\omega tdt만 살아남는다.

즉,∫0Tf(t)cos⁡nωtdt=∫0Tancos⁡2nωtdt=an∫0Tcos⁡2nωtdt=T2an\int_{0}^{T}f(t)\cos n\omega tdt=\int_{0}^{T}a_n\cos^2 n\omega tdt=a_n\int_{0}^{T}\cos^2 n\omega tdt=\frac{T}{2}a_n이므로, an=2T∫0Tf(t)cos⁡nωtdta_n=\frac{2}{T}\int_{0}^{T}f(t)\cos n\omega tdt

b1b_1~b∞b_\infin구하기

f(t)=a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )f(t) = a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)

이번엔 양변에 sin⁡nωt\sin n\omega t를 곱한 후 적분한다.

∫0Tf(t)cos⁡nωtdt=∫0T[a0+(a1cos⁡ωt+a2cos⁡2ωt+⋯+ancos⁡nωt+… )+(b1sin⁡ωt+b2sin⁡2ωt+⋯+bnsin⁡nωt+⋯ )]sin⁡nωtdt=∫0Ta0sin⁡nωtdt+a1∫0Tcos⁡ωtsin⁡nωtdt+a2∫0Tcos⁡2ωtsin⁡nωtdt+⋯+b1∫0Tsin⁡ωtsin⁡nωtdt+b2∫0Tsin⁡2ωtsin⁡nωtdt+…\int_{0}^{T}f(t)\cos n\omega tdt = \int_{0}^{T}[a_0 + (a_1\cos\omega t+a_2\cos2\omega t+\dots+a_n\cos n\omega t+\dots)\\ + (b_1\sin\omega t+b_2\sin2\omega t+\dots+b_n\sin n\omega t+\cdots)]\sin n\omega tdt\\=\int_{0}^{T}a_0\sin n\omega tdt+a_1\int_{0}^{T}\cos \omega t\sin n\omega tdt+a_2\int_{0}^{T}\cos 2\omega t\sin n\omega tdt + \dots + b_1\int_{0}^{T}\sin \omega t\sin n\omega tdt+b_2\int_{0}^{T}\sin 2\omega t\sin n\omega tdt+\dots

여기서 ∫0Tsin⁡mωsin⁡nωtdt=0\int_{0}^{T}\sin m\omega \sin n\omega tdt=0, ∫0Tcos⁡mωsin⁡nωtdt=0\int_{0}^{T}\cos m\omega \sin n\omega tdt=0, ∫0Tsin⁡nωtdt=0\int_{0}^{T} \sin n\omega tdt=0이기 때문에, ∫0Tbnsin⁡2nωtdt\int_{0}^{T}b_n\sin^2 n\omega tdt만 살아남는다.

즉,∫0Tf(t)sin⁡nωtdt=∫0Tbnsin⁡2nωtdt=bn∫0Tsin⁡2nωtdt=T2bn\int_{0}^{T}f(t)\sin n\omega tdt=\int_{0}^{T}b_n\sin^2 n\omega tdt=b_n\int_{0}^{T}\sin^2 n\omega tdt=\frac{T}{2}b_n이므로, bn=2T∫0Tf(t)sin⁡nωtdtb_n=\frac{2}{T}\int_{0}^{T}f(t)\sin n\omega tdt

정리 후 결과 대입

정리하자면 다음과 같다.
a0=1T∫0Tf(t)dta_0=\frac{1}{T}\int_{0}^{T}f(t)dt

an=2T∫0Tf(t)cos⁡nωtdta_n=\frac{2}{T}\int_{0}^{T}f(t)\cos n\omega tdt

bn=2T∫0Tf(t)sin⁡nωtdtb_n=\frac{2}{T}\int_{0}^{T}f(t)\sin n\omega tdt

이를 f(t)=a0+∑n=1∞(ancos⁡nωt+bnsin⁡nωt)f(t) = a_0 + \sum_{n=1}^{\infin}(a_n\cos n\omega t+b_n\sin n\omega t) 이식에 대입하면 다음과 같다.

f(t)=1T∫0Tf(t)dt+∑n=1∞((2T∫0Tf(t)cos⁡nωtdt)cos⁡nωt+(2T∫0Tf(t)sin⁡nωtdt)sin⁡nωt)f(t) = \frac{1}{T}\int_{0}^{T}f(t)dt + \sum_{n=1}^{\infin}((\frac{2}{T}\int_{0}^{T}f(t)\cos n\omega tdt)\cos n\omega t+(\frac{2}{T}\int_{0}^{T}f(t)\sin n\omega tdt)\sin n\omega t)

ω=2πn\omega = 2\pi n으로 각속도로 나타낼 수 있기에 이를 대입하면 다음과 같다.

f(t)=1T∫0Tf(t)dt+∑n=1∞((2T∫0Tf(t)cos⁡2πnωtdt)cos⁡2πnωt+(2T∫0Tf(t)sin⁡2πnωtdt)sin⁡2πnωt)f(t) = \frac{1}{T}\int_{0}^{T}f(t)dt + \sum_{n=1}^{\infin}((\frac{2}{T}\int_{0}^{T}f(t)\cos 2\pi n\omega tdt)\cos 2\pi n\omega t+(\frac{2}{T}\int_{0}^{T}f(t)\sin 2\pi n\omega tdt)\sin 2\pi n\omega t)

오일러 공식

오일러는 가우스가 구상한 실수와 허수축이 있는 복소평면에서 공식을 하나 찾았다.

eiπ=−1e^{i\pi} = -1 세상에서 가장 멋진 수식이다.

그 이유를 알아보자.

유도


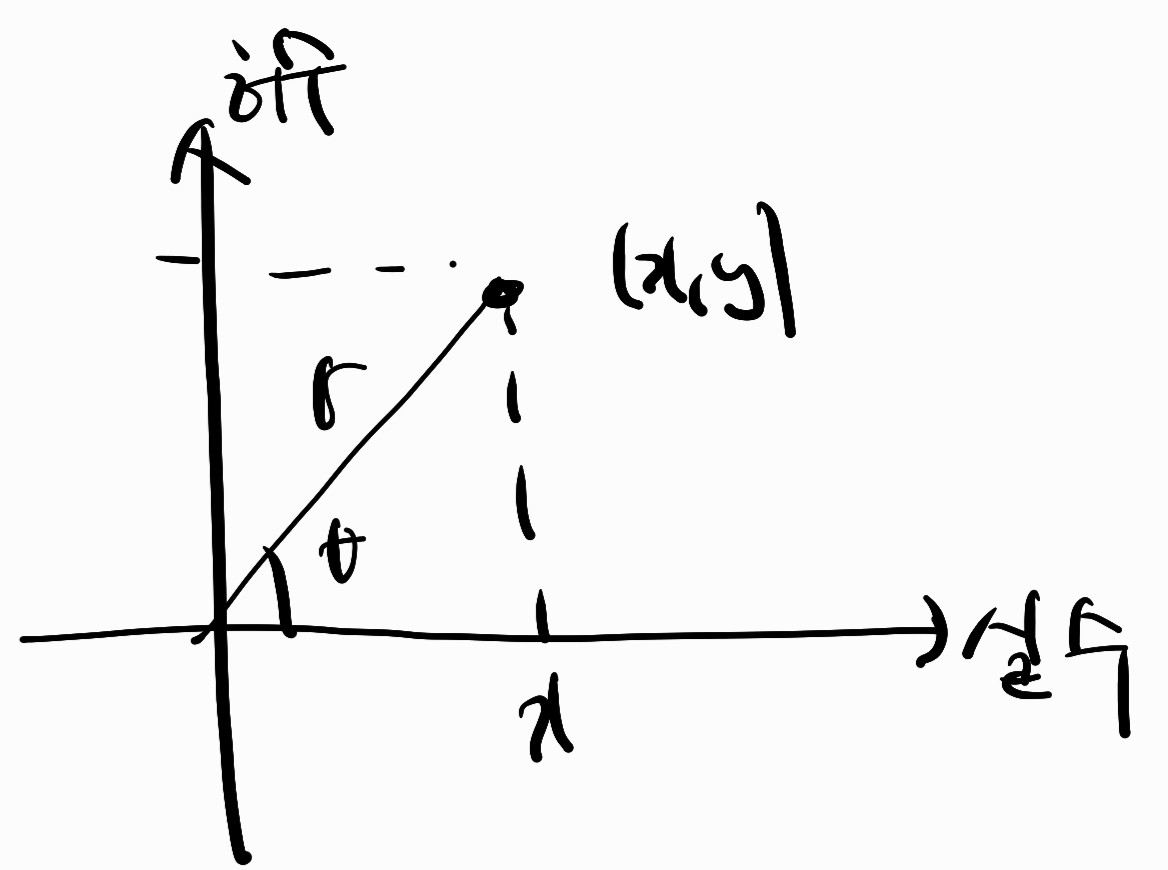
복소평면의 (x,y)(x, y)에 점이 있다고 하자.

원점과 점까지의 거리는 rr이라고 하면, x=rcos⁡θ,y=rsin⁡θx=r\cos\theta, y=r\sin\theta로 나타낼 수 있다.

그리고 복소평면의 점은 복소수로 나타낼 수 있다.

x+iy=rcos⁡θ+irsin⁡θx + iy = r\cos\theta+ir\sin\theta 이를 AA라고 둔다.

이 점은 원점과 r=1r=1이라고 가정한다. 그래서 A=cos⁡θ+isin⁡θA=\cos\theta+i\sin\theta이다.

양변에 θ\theta로 미분하면 dAdθ=icos⁡θ−sin⁡θ=i(isin⁡θ+cos⁡θ)=iA\frac{dA}{d\theta}=i\cos\theta-\sin\theta=i(i\sin\theta+\cos\theta)=iA이다.

양변에 dθA\frac{d\theta}{A}를 곱해주면 dAA=idθ\frac{dA}{A}=id\theta이다.

서로 적분을 진행하면 lnA=iθlnA=i\theta이므로 A=eiθA=e^{i\theta}이다.

즉, cos⁡θ+isin⁡θ=eiθ\cos\theta+i\sin\theta=e^{i\theta}가 된다.

삼각함수와 오일러 공식

cos⁡θ+isin⁡θ=eiθ\cos\theta+i\sin\theta=e^{i\theta} 에서 θ\theta자리에 −θ-\theta를 넣어보자.

cos⁡−θ+isin⁡−θ=e−iθ\cos-\theta+i\sin-\theta=e^{-i\theta} 가 된다.

주기 함수의 성질로 인해 cos⁡θ−isin⁡θ=e−iθ\cos\theta-i\sin\theta=e^{-i\theta} 이렇게 유도된다.

cos⁡θ+isin⁡θ=eiθ\cos\theta+i\sin\theta=e^{i\theta}식과 유도된 식을 합치고 빼고를 하면

cos⁡θ=eiθ+e−iθ2\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}, sin⁡θ=eiθ−e−iθ2i\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}을 유도할 수 있다.

오일러 공식을 푸리에 급수에 대입

오일러 공식을 약간 변환한 cos⁡nωt=einωt+e−inωt2\cos n\omega t=\frac{e^{in\omega t}+e^{-in\omega t}}{2}, sin⁡nωt=einωt−e−inωt2i\sin n\omega t=\frac{e^{in\omega t}-e^{-in\omega t}}{2i}을 대입해보자.

f(t)=a0+∑n=1∞(ancos⁡nωt+bnsin⁡nωt)=a0+∑n=1∞(an(einωt+e−inωt2)+bn(einωt−e−inωt2i))f(t) = a_0 + \sum_{n=1}^{\infin}(a_n\cos n\omega t+b_n\sin n\omega t)\\=a_0+\sum_{n=1}^{\infin}(a_n(\frac{e^{in\omega t}+e^{-in\omega t}}{2})+b_n(\frac{e^{in\omega t}-e^{-in\omega t}}{2i}))

여기서 einωte^{in\omega t}와 e−inωte^{-in\omega t}를 따로 묶어서 다시 전개한다.

f(t)=a0+∑n=1∞(an(einωt+e−inωt2)+bn(einωt−e−inωt2i))=a0+∑n=1∞(an−bni2(einωt)−an+bni2(e−inωt))f(t)=a_0+\sum_{n=1}^{\infin}(a_n(\frac{e^{in\omega t}+e^{-in\omega t}}{2})+b_n(\frac{e^{in\omega t}-e^{-in\omega t}}{2i}))\\=a_0+\sum_{n=1}^{\infin}(\frac{a_n-b_ni}{2}(e^{in\omega t})-\frac{a_n+b_ni}{2}(e^{-in\omega t}))

그리고 시그마의 범위를 00~∞\infin이 아닌 −∞-\infin~∞\infin으로 확장시키기 위해, e−inωte^{-in\omega t}부분이 있는 곳을 nn자리에 −n-n을 대입해준다.

f(t)=a0+∑n=1∞(an−bni2(einωt)−an+bni2(e−inωt))=a0+∑n=1∞(an−bni2einωt)+∑n=−1−∞(a−n−b−ni2einωt)f(t)=a_0+\sum_{n=1}^{\infin}(\frac{a_n-b_ni}{2}(e^{in\omega t})-\frac{a_n+b_ni}{2}(e^{-in\omega t}))\\=a_0+\sum_{n=1}^{\infin}(\frac{a_n-b_ni}{2}e^{in\omega t})+\sum_{n=-1}^{-\infin}(\frac{a_{-n}-b_{-n}i}{2}e^{in\omega t})

여기에 아까 푸리에 급수 정리 파트에서 구한 3가지 요소를 대입한다.
a0=1T∫0Tf(t)dta_0=\frac{1}{T}\int_{0}^{T}f(t)dt

an=2T∫0Tf(t)cos⁡nωtdta_n=\frac{2}{T}\int_{0}^{T}f(t)\cos n\omega tdt

bn=2T∫0Tf(t)sin⁡nωtdtb_n=\frac{2}{T}\int_{0}^{T}f(t)\sin n\omega tdt

참고로 이식도 cos⁡nωt=einωt+e−inωt2\cos n\omega t=\frac{e^{in\omega t}+e^{-in\omega t}}{2}, sin⁡nωt=einωt−e−inωt2i\sin n\omega t=\frac{e^{in\omega t}-e^{-in\omega t}}{2i}를 대입해서

a0=1T∫0Tf(t)dta_0=\frac{1}{T}\int_{0}^{T}f(t)dt

an=2T∫0Tf(t)(einωt+e−inωt2)dt=1T∫0Tf(t)(einωt+e−inωt)dta_n=\frac{2}{T}\int_{0}^{T}f(t)(\frac{e^{in\omega t}+e^{-in\omega t}}{2})dt=\frac{1}{T}\int_{0}^{T}f(t)(e^{in\omega t}+e^{-in\omega t})dt

bn=1T∫0Tf(t)(einωt−e−inωti)dtb_n=\frac{1}{T}\int_{0}^{T}f(t)(\frac{e^{in\omega t}-e^{-in\omega t}}{i})dt 로 바꿔주고 대입해주면..

f(t)=∑−∞∞(∫0Tf(t)(e−inωt)dt)einωtf(t)=\sum_{-\infin}^{\infin}(\int_0^Tf(t)(e^{-in\omega t})dt)e^{in\omega t}으로 유도된다.

결론

f(t)=∑−∞∞(∫0Tf(t)(e−inωt)dt)einωtf(t)=\sum_{-\infin}^{\infin}(\int_0^Tf(t)(e^{-in\omega t})dt)e^{in\omega t}

profile
milkbottle
이전 포스트

API의 결과에 따라 다른 결과를 보여주고 싶어!

다음 포스트

모달창을 만들어보자

0개의 댓글