푸리에 변환

이전에 푸리에 급수를 유도한 적이 있다.

푸리에와 관련된 것들은 여러 신호가 섞여있는 신호를 진동수 레벨로 변환해서 찾는 기술이다.

성질

연속적(continuous)

시간을 연속적으로 0초부터 10초사이가 있다고 하자.

그 사이 모든 실수의 영역 0.0000....1 .. 이런수는 없지만 엄청 작은 단위의 숫자를 대입해도 값이 나오는 것을 연속적이라고 한다.

이러한 값들 모두를 함수로 나타내는 것을 연속적이라고 하며, CT(Continuous Time)이라고 한다.

이산적(discrete)

시간을 0초부터 10초사이에 0, 1, 2, 3, ... 딱딱 정수로 나누어 샘플링 한 경우를 이산적이라고 하며, DT(Discrete Time) 이라고 한다.

주기성(periodic)

신호는 주기성일 수도 있고 비주기성일 수도 있다.

주기성 신호는 sin파, cos파같은 신호들을 뜻한다. 누가봐도 주기가 드러나는 신호이다.

이런 신호들은 푸리에 급수(FS: Fourier Series)를 통해 진동수를 찾을 수 있다.

비주기성(aperiodic)

비주기성은 주기가 무한대라고 볼 수 있다.

푸리에 변환(FT: Fourier Transform)을 비주기성일 때 사용한다.

정리

총 4가지의 패턴이 나온다.

1. 연속적 주기적 = Contious Time + Fourier Series = CTFS
2. 이산적 주기적 = Discrete Time + Fourier Series = DTFS
3. 연속적 비주기적 = Contious Time + Fourier Transform = CTFT
4. 이산적 비주기적 = Discrete Time + Fourier Transform = DTFT

라고 표현한다.

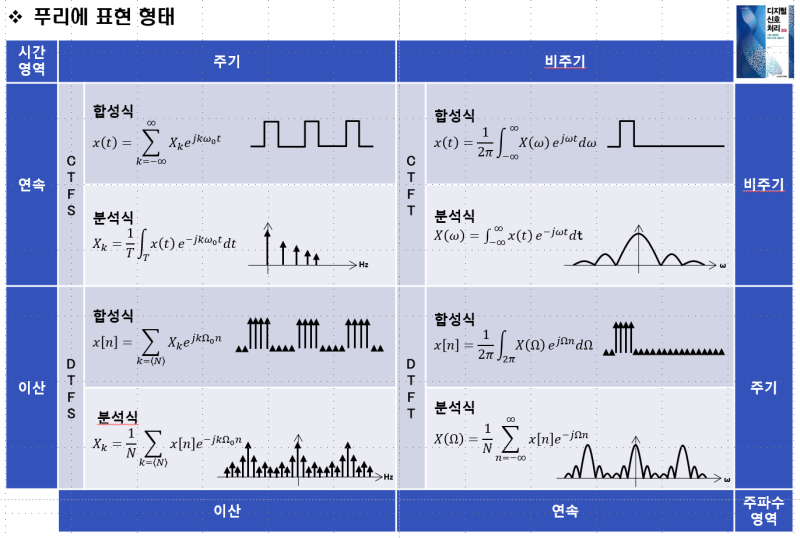
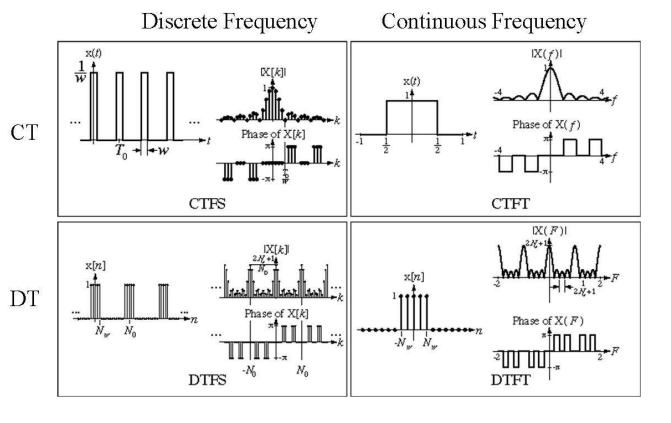
이들을 이미지로 표현하면 다음과같다.

CTFS

연속적이고 주기적인 신호를 변환하면 진동수레벨은 이산적이고 비주기적이다.

DTFS

이산적이고 주기적인 신호를 변환하면 진동수레벨은 이산적이고 주기적이다.

CTFT

연속적이고 비주기적인 신호를 변환하면 진동수레벨은 연속적이고 비주기적이다.

DTFT

이산적적이고 비주기적인 신호를 변환하면 진동수레벨은 연속적이고 주기적이다.

진동수레벨의 샘플링

한단계 더 나아가 진동수레벨로 변환한 그래프를 이산적으로 샘플링할 수 있다.

위의 4가지 공식 중에서 진동수레벨에서 샘플링을 하려면 연속적인 공식이 있다.

바로 CTFT와 DTFT이다. 이 둘은 진동수레벨에서는 연속적이다.

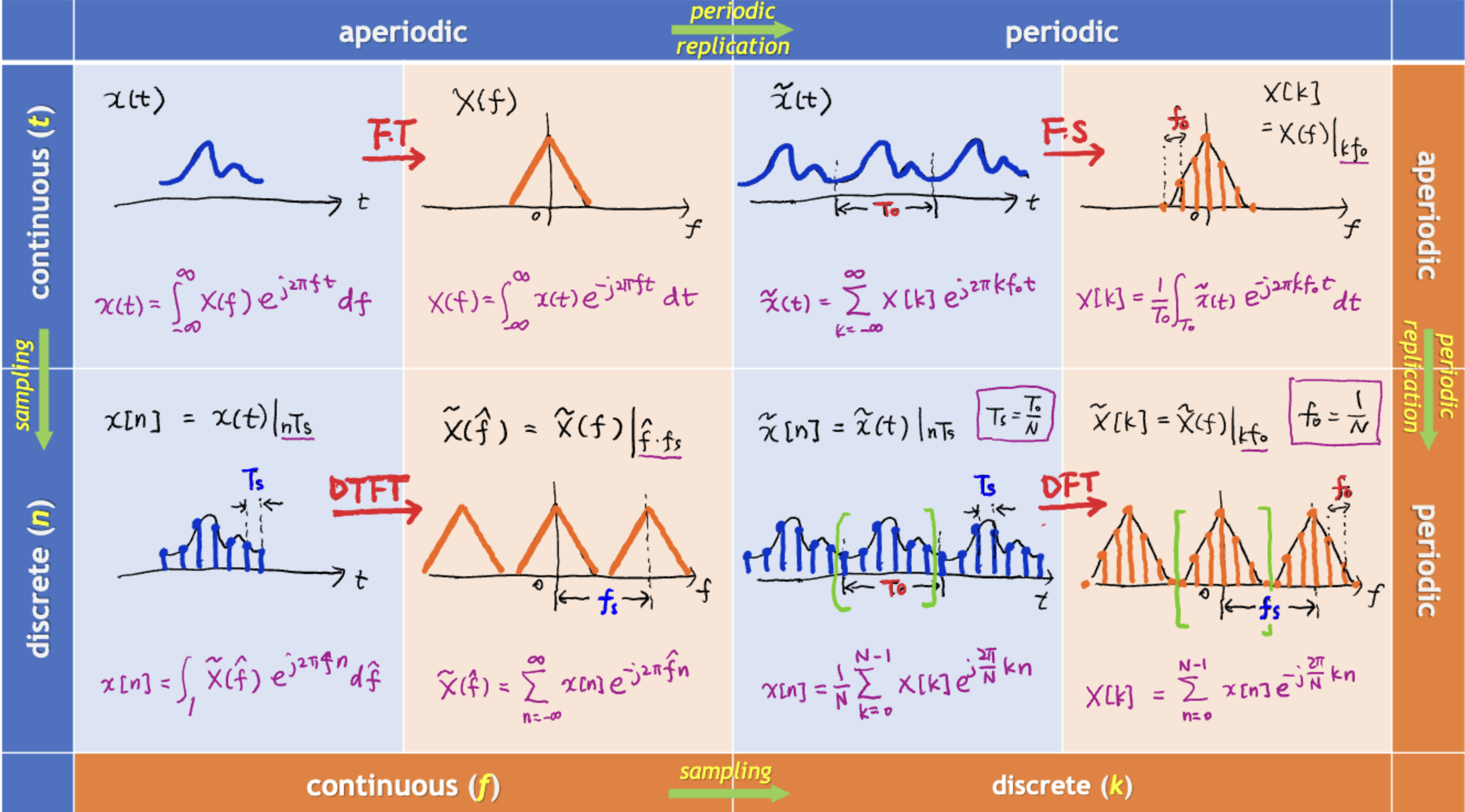
DFS

CTFT를 통해 변환한 진동수레벨의 그래프를 진동수를 기준으로 샘플링한 것을 의미한다.

진동수는 $f_0$ 기준으로 샘플링하였다.

DFT

DTFT를 통해 변환한 진동수레벨의 그래프를 진동수 기준으로 샘플링한 것을 의미한다.

똑같이 $f_0$ 기준으로 샘플링하였다.

헷갈리는 부분 정리

CTFS vs DFS 그리고 DTFS vs DFT

두 그래프는 비슷해 보이지만, CTFS는 진동수레벨의 결과가 이산적일 뿐 각 진동수 사이의 간격은 일정하지 않을 수 있다.

f=1일때 5, f=2일때 Nan, f=3일때 3, f=4일때 1 이런식으로 제멋대로 값이 분포한다.

하지만 DFS는 CTFT로 변환한 진동수레벨의 그래프를 진동수 기준으로 샘플링 한 것이다.

$f_0=1$이라면, f=1일때 5, f=2일때 0, f=3일때 3, .. .이런식으로 진동수가 1이 차이날때마다 모든값이 매핑되는 것이다.

마찬가지로, DTFS vs DFT도 같은 설명을 통해 이해가 될 것이다.

DTFT vs DFT vs FFT

• DTFT: 신호를 이산적으로 샘플링하고, 이 신호가 비주기적이어서 푸리에 변환을 한 것
• DFT: DTFT한 결과로 나온 연속적인 진동수그래프를 진동수로 샘플링 한 것
• FFT: Fast Fourier Transform으로 DFT를 많이 쓰는데 이를 빠르게 해준 기술