Introduction

• 이미지 데이터는 색을 포함하는 2차원의 픽셀 격자로 표현된다. 따라서 하나의 픽셀은 하나의 튜플(벡터)로 표현된다
• 픽셀의 공간적인 정보를 고려하지 않고, 이미지를 flatten하여 처리하는 기존의 MLP로서는 해석능력의 한계를 갖게 되는 것이다
• 이러한 이유로 CNN, Convolutional Neural Network는 고안되어 설계되었다. 그 결과 CNN는 컴퓨터 비전 분야에서 압도적인 지위를 갖고 있다
• CNN는 MLP에 비해 적은 파라미터를 활용하기 때문에, 계산에있어 더 경제적이다.
  - 그 결과 CNN는 1차원-시퀀스 데이터인 오디오,텍스트,시계열분석등 기존 RNN이 활용되는 영역에서도 응용되고 있다.
  - CNN는 그래프-구조의 데이터와의 응용을 통하여 추천시스템에 활용되고 있기도 하다
  

CNN과 불변량

• 예시: 윌리를 찾아라
  - CNN을 어떻게 설계할 것인가는 '윌리를 찾아라' 라는 게임에서부터 영감을 받을 수 있다
  - 수많은 인중들로부터, 조금은 어색한 위치에 있는 윌리를 찾는 이 게임은 윌리가 독특한 복장을 하고 있음에도, 수많은 방해요소들 때문에 의외로 찾기 어렵다는 점이 있다.
  - 여기서 주는 통찰은 윌리를 찾기 위해선 윌리가 어디에 위치해 있는가와 관련없이 그 복장에만 집중해야 한다는 점이다. 이것을 수학적 용어로 표현하면 spatial invariance 라고 한다
  1. Translation invariance: 윌리가 어떤 곳에 위치해 있건 상관없다는 것은, 윌리의 이미지를 인식하는데 얼마나 평행이동translation는 고려하지 않음을 의미한다(회전없이, 물체를 가로-세로-높이 임의의 방향으로 이동시키는 운동. 다만 이미지 인식에서 물체가 얼마나 회전했는가와 상관없이 동일하게 인식되어야 할 것이므로, 물체의 강체 운동 rigid motion(변형이 발생되지 않은 물체의 운동)에 물체 인식이 영향을 받지 않아야 한다로 조건이 확장되야 할 것이다)
  2. localty principle: 물체를 인식하는데엔 관찰하는 영역 외에 영역들의 정보가 고려되어선 안된다.

불변량을 고려한 CNN 설계

• 조건
  - 2차원 이미지 입력값을 $\boldsymbol{X}$ , 은닉층의 표현값을 $\boldsymbol{H}$ 라고 하자
  - 2차 텐서 $\boldsymbol{U}$ 를 편향값으로, 4차텐서 $\boldsymbol{W}$ 를 가중치 텐서라고 하자.
  그렇다면 tensor contraction에 의해
• 정의
  - 위치 $i,j$ 에 대한 은닉층의 표현값은
  - $[\boldsymbol{H}]_{i,j}=[\boldsymbol{U}]_{i,j}+\displaystyle\sum_{k}^{}{\displaystyle\sum_{l}^{}{[\boldsymbol{W}]_{i,j,k,l}[\boldsymbol{X}]_{k,l}}}$
  - $=[\boldsymbol{U}]_{i,j}+\displaystyle\sum_{a}^{}{\displaystyle\sum_{b}^{}{[\boldsymbol{V}]_{i,j,a,b}[\boldsymbol{X}]_{i+a,j+b}}}$
  - $\boldsymbol{W}$ 로부터 $\boldsymbol{V}$ 로 바뀐것은 단순히 리인덱싱 $k=i+a,l=j+b$ 으로 바꾸는 겉모습만 바꾸는 것에 지나지 않는다. 다만 이렇게 하는 것은 수학의 convolution 정의와 유사성을 보여주는데 있다
• Tranlsation Invariance 적용
  - 이미지가 얼마나 평행이동했는지 고려하지 않는다는 것은 가중치 텐서 $\boldsymbol{V}$ 와 편향 $\boldsymbol{U}$가 입력값의 위치정보 $i,j$ 에 의존하지 않음을 의미한다 따라서
  - $[\boldsymbol{H}]_{i,j}=u+ \displaystyle\sum_{a}^{}{\displaystyle\sum_{b}^{}{[\boldsymbol{V}]_{a,b}[\boldsymbol{X}]_{i+a,j+b}}}$
• Locality 적용
  - 우리는 이미지를 인식하는데 이미지의 전체 영역이 아닌 국소영역만 살펴볼 것이다. 이는 연산에 참여하는 가중치 텐서 $\boldsymbol{V}$ 와 입력값 $\boldsymbol{X}$ 가 일부만 참여한다는 의미로, 따라서
  - $[\boldsymbol{H}]_{i,j}=u+\displaystyle\sum_{a=-\Delta}^{\Delta}{\displaystyle\sum_{b=-\Delta}^{\Delta}{[\boldsymbol{V}]_{a,b}[\boldsymbol{X}]}_{i+a,j+b}}$
• 결과
  - Translation Invariance를 활용하여 입력값의 위치정보를 고려하지 않음으로써 $\displaystyle\frac{1}{10 ^{3} \times 10 ^{3}}$ 곱만큼으로 파라미터수를 줄일 수 있었고, Locality를 활용하여 $\displaystyle\frac{\Delta ^{2}}{10 ^{3}\times 10 ^{3}}$ 곱만큼으로 파라미터수를 줄일 수 있게 되었다.
  - 이런 연산의 성질덕분에 일반적으로 $\Delta$는 10이하로 잡는다

수학에서의 합성곱Convolution 정의

• 상세한 정의는 [[2.Convolution]]
• 수학에서 합성곱 $f,g:\mathbb{R} ^{d} \to \mathbb{R}$ 는 다음과 같이 정의된다
  - $(f *g)(\boldsymbol{x})=\displaystyle\int_{}^{}{f(\boldsymbol{z})g(\boldsymbol{x}-\boldsymbol{z})d \boldsymbol{z }}$
  - $(f*g)(i)=\displaystyle\sum_{a}^{}{f(a)g(i-a)d \boldsymbol{z}}$
• 2차원 텐서에 대하여는 다음과 같이 행렬곱이 정의될 수 있다
  - $(f*g)(i,j)=\displaystyle\sum_{a}^{}{\displaystyle\sum_{b}^{}{f(a,b)}g(i-a,j-b)}$
• 이는 제법 $[\boldsymbol{H}]_{i,j}=u+\displaystyle\sum_{a=-\Delta}^{\Delta}{\displaystyle\sum_{b=-\Delta}^{\Delta}{[\boldsymbol{V}]_{a,b}[\boldsymbol{X}]}_{i+a,j+b}}$ 과 유사한 형태를 띈다.
• CNN에서 말하는 Convolution은 엄격히 말하면 Convolution보단 cross-correlation이란 연산의 정의에 부합한다

채널

• 다시 윌리의 예제로 돌아가자
  - 은닉층에선 '윌리스러움'을 측정할 수 있게 될지도 모른다
• 이미지를 $1024 \times 1024$ 개의 픽셀로 이루어져 있고, 색이 빨강,초록,파랑으로 이루어져있다고 하자
  - 이 경우 입력층 텐서와 은닉층 텐서 모두 3차원이 되고, 가중치만이 2차텐서로 존재할 것이다
  - 이렇게 회면 은닉층은 각 픽셀 위치에 대한 정보보단, 측정 특징에 대한 정보를 담는 것이 좋을것이다.
• 채널을 고려한 CNN의 연산은 다음과 같다
  - $[\boldsymbol{H}]_{i,j,d}=\displaystyle\sum_{a=-\Delta}^{\Delta}{\displaystyle\sum_{b=-\Delta}^{\Delta}{\displaystyle\sum_{c}^{}{[\boldsymbol{V}]_{a,b,c,d}[\boldsymbol{X}]_{i+a,j+b,c}}}}$
  - 여기서$c$는 input channel, $d$ 는 output channel 의 크기이다. 이식은 CNN에 대한 일반적인 정의가 된다

CNN의 여러 연산들과 용어

Block

• 하나의 레이어, 여러개의 레이어, 모델 전체를 이를 수 있는말
• 소프트웨어의 관점에선, 블록은 하나의 클래스이다.
  - 블록의 서브클래스로서 반드시 forward 메소드가 존재하여 입력값을 출력값을 변환함과 동시에 파라미터를 저장할 수 있어야 한다
  - 블록의 서브클래스로서 반드시 backward 메소드가 존재하여, gradient를 계산할 수 있어야 한다. 다만 대부분의 라이브러리들은 autograd package를 제공하기 때문에, backward는 따로 정의할 필요가 없을 수 있다

Receptive Field

• 다음 층에 영향을 미치는 이전층의 입력뉴런 공간 크기
• Dialated Convolution의 경우 픽셀이 서로 간격을 갖고 띄엄띄엄 존재하는데, 이때 모서리 끝 사이의 길이로 Receptive Field의 크기를 측정한다

feature map

• 입력으로부터 커널을 사용하여 합성곱 연산을 통해 나온 결과

Activation map

• 앞서 나온 Feature map에 활성함수를 적용하여 나온 결과
• Hidden Layer 연산의 최종결과물이다

convolution시 고려되는 요소

• 합성곱시 다음과 같은 과정을 거친다
  1. 입력값이 되는 레이어에 지정된 Padding 크기 만큼 상하좌우로 0인 원소로 체워 텐서의 크기를 키운다
  2. 입력 텐서에서 Kernel Size와 동일한 크기의 국소 영역(윈도우)를 정하고, Kernel과 element-wise 곱셈을 시행하고, 다 더한다. 그 결과를 새로운 출력 텐서의 한 원소값으로 정한다
  3. 2번이 끝났을때, 지정된 Stride 값 만큼 입력텐서의 국소영역을 이동시킨다
  - 해당 연산의 결과로 출력텐서는 $o _{h}=Floor(\displaystyle\frac{i _{h}+2p _{h}-k _{h}}{s _{h}}+1)$ , $o _{w}=Floor(\displaystyle\frac{i _{w}+2p _{w}-k _{w}}{s _{w}}+1)$ 의 크기를 갖는다
• Kernel Size
  - Kernel Size는 Convolution 연산을 통해 출력텐서의 크기를 제어할 수 있고, 픽셀 하나가 아닌 지정된 크기만큼의 영역 정보를 종합하여 특징을 축출할 수 있게 한다.
• Padding
  - Padding은 출력텐서의 크기를 제어하는 또다른 방법이다. 지정된 Padding 크기 만큼 상하좌우로 0인 원소로 체운다
  - CNN는 주로 1,3,5,7등의 홀수를 활용한다
• Stride
  - 필터가 이동하는 간격을 의미한다
  - 컴퓨터 연산의 효율성을 위하여 주로 사용한다

CNN의 Computational Cost

• 조건
  - $c _{l-1}$ : 이전층의 채널수
  - $c _{l}$ : 현재층의 채널수
  - $m _{l-1}$ : 이전 피처맵 크기
  - $m _{l}$ : 현재 피처맵 크기
  - $k$ : 필터 크기
• 파라미터 수
  - $k \times k \times c _{l-1} \times c _{l}+c _{l}$
  - 가중치의 수로 학습 이후 메모리에 저장되는 값이다
  - 이때 두번째 $c _{l}$ 는 bias 파라미터 갯수이다
• $[\boldsymbol{Y}]_{i,j,l}=\displaystyle\sum_{\alpha}^{}{\displaystyle\sum_{\beta}^{}{}}\displaystyle\sum_{k}^{}{}[\boldsymbol{K}]_{\alpha,\beta,k,l}[\boldsymbol{X}]_{i+\alpha,j+\beta,k}$
  - 텐서 ${Y}$ 을 계산하는데 필요한 연산량 $k \cdot k \cdot c _{l} \cdot c _{l-1} \cdot m _{l-1}$

Multiple Input Channels /Output Channels

• 현재까지는 입력 데이터의 채널수에 맞춰, 커널또한 동일한 채널수를 갖도록 설계하였다
  - 그러나 신경망이 깊어질수록 채널 차원수를 높이는 방법으로 설계할 수 있다.
  - 이는 각 채널마다 대응되는 피쳐를 캐치해내는 것으로 작동할 것이라 볼 수 있다
• $1 \times 1$ Convolutional Layer
  -
  - $k _{h}= k _{w}=1$ 인 이 커널은 기존 레이어가 갖는 채널수 $c _{i}$ 를 채널수 $c _{o}$ 로 변환해줄 때 사용되는 레이어이다
  - 그 결과 기존 레이어의 높이와 폭 길이는 보존된다는 특징을 갖고 있다

Pooling

• Convolution을 거쳐 나온 텐서의 크기를 resizing하여 새로운 텐서를 얻는 방법이다.
  - 이 연산에선 채널수가 변화하지 않는다
• 신경망이 깊어질수록 receptive field의 영역은 더 넓게 민감하게 된다. 이는 convolution 커널이 더 넓은 영역을 커버하게 됨으로써 발생하는 일이다 그 결과
  - 필요한 파라미터의 수가 줄어들게 되고 이는 과적합을 줄이는데 도움이 된다
  - 또한 지역적 이동에 노이즈를 줌으로써 일반화 성능이 향상된다
• Pooling layer의 특징
  - 학습시킬 파라미터가 존재하지 않는다
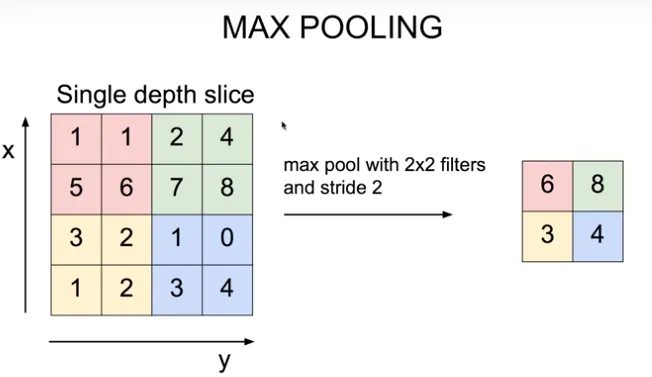
  - 윈도우 내 가장 큰 숫자를 찾는 Maximum Pooling과 윈도우 내 숫자들을 평균내는 Average Pooling 둘로 나뉜다. (Maximum Pooling은 인지신경과학에서 연구된 결과에서 영감을 얻었다고 한다)
  - 연산결과 $o _{h} =Floor\left(\displaystyle\frac{i _{h}-k _{h}}{s _{h}}+1\right)$ , $o _{w} =Floor\left(\displaystyle\frac{i _{w}-k _{w}}{s _{w}}+1\right)$ 의 크기를 갖는다
• 예
  -

기초 CNN 구현하기

Convolution(Cross-Correlation) 함수

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """Compute 2D cross-correlation."""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

CNN 레이어 클래스

• __init__ : 가중치 weight 와 편향 bias 를 저장한다
• forward : 합성곱 corr2d 를 수행한다

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

Padding과 Stride를 고려한 CNN 레이어 클래스

• torch.nn.LazyConv2d 에서 제공한다
  - kernel_size : convolution kernel의 크기를 정한다
  - stride : stride 크기를 정한다
  - padding : padding 크기를 정한다

1x1 Convolution 함수

• $[\boldsymbol{K}\boldsymbol{X}]_{ijl}=[\boldsymbol{K}]_{lk}[\boldsymbol{X}]_{kij}$

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    """각 채널의 2차텐서를 1차텐서로 flatten하게 만든다"""
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # Matrix multiplication in the fully connected layer
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y1
"""result)
tensor([[[ 0.5369, -2.3193, -1.6800],
         [-0.5350,  1.6553,  1.1178],
         [ 3.4678,  2.4251,  2.4274]],

        [[ 2.5284, -1.1243, -2.6959],
         [-1.3012,  1.7203,  2.1077],
         [ 1.5489,  1.1090,  3.6274]]])
"""

풀링 함수

• torch.nn.MaxPool2d 에서 제공함

import torch
from torch import nn
from d2l import torch as d2l

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y