🔒 문제
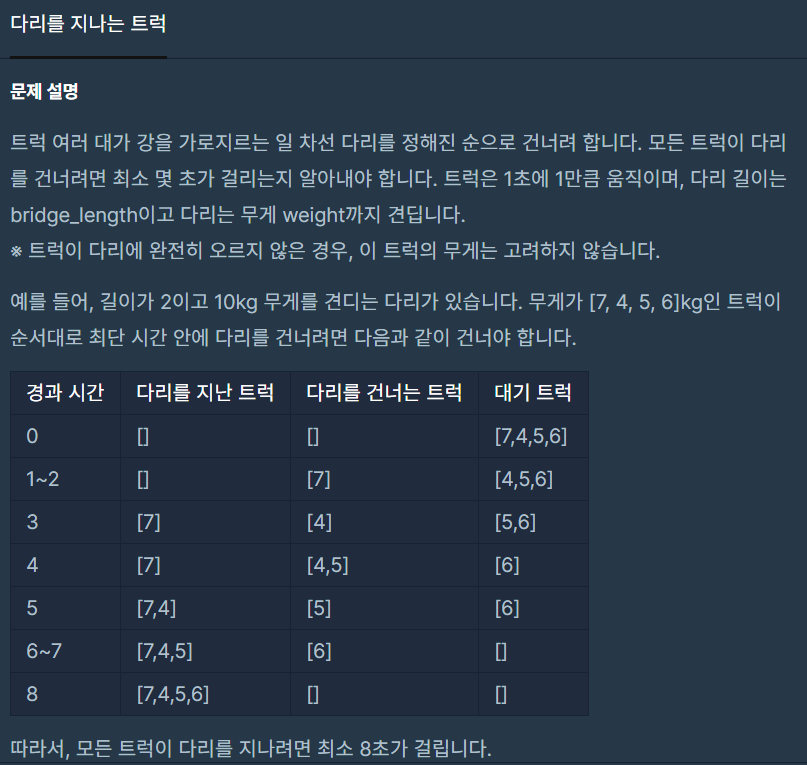
모든 트럭이 다리를 지나는데 걸리는 소요시간을 return 하시오
😵💫 실수
풀이 1에서 forEach
(1) 케이스를 다리위로 트럭을 올림 (2) 이동시킴으로 했는데
둘중 하나만 실행하기 때문에
이동시키고 다시 올리는 과정이 빠지게됨.
풀이 2에서 트럭을 다리 위에 올릴 때까지 Collections.rotate 를 할 필요는 없음
=> 마지막 원소 삭제하고 첫원소 추가시켜주면 rotate 한 효과와 같음.
💭 생각의 흐름
현재 다리 위의 무게를 keep 한다.
(1) 무게가 허용하는 선 내에서 모든 트럭 탑재 (moveCount++)
(2) 올라간 트럭들중 맨 뒤 (제일 다리 끝에 가까운 트럭)의 위치를 구하고 다리길이 - 위치 - 1 == 남은 거리 (남은 moveCount) ,, 남은 거리만큼 모든 트럭 이동
(3) (0)~(2) 모든 트럭을 올릴 때 까지 반복
🚨 반복을 탈출하는 시점은 맨 마지막 트럭을 다리 위로 올리자 마자이다!
(4) 현재까지 이동거리 + 다리 길이 == 총 소요시간
😂 풀이 (오답)
import java.util.*
class TrucksOnBridge {
fun solution(bridge_length: Int, weight: Int, truck_weights: IntArray): Int {
var moveCount = 0
var currentWeightOnBridge = 0
// ArrayList vs LinkedList 선정 근거
// arrayList 는 참조, 맨 뒤 append 자주할 때, 특히 맨 앞자리에 삽입은 지옥임 == O(N)
// LinkedList, Queue 는 맨 앞과 뒤 추가 삭제에 비용이 들지 않음 O(1). (대신 index 참조가 오래걸림 == O(N))
val bridgeLinkedList = LinkedList<Int>(List<Int>(bridge_length){0}) // 0으로 초기화
// 1. 이동시 다음 번 순서가 다리에 곧바로 오를 수 있는지 무게 검사 (제한 무게 vs 현재 다리 위 무게 + 다음놈 무게)
truck_weights.forEach {
// 올려 태우는 경우 먼저 1칸씩 이동시키고 올려태움, 맨 마지막 자리가 0인경우 (다리 끝에 도착한 경우) 삭제시킴.
if (weight >= currentWeightOnBridge + it) {
moveCount++
with (bridgeLinkedList) {
Collections.rotate(this, 1)
this.removeFirst()
this.addFirst(it)
currentWeightOnBridge += it
}
} else {
// 무게 제한으로 그냥 이동시키는 경우 다리의 맨 선두주자를 일단 도착시켜야함.
// 맨 선두주자 도착시까지 이동거리 == 다리 길이 - 현재 위치 인덱스
with (bridgeLinkedList) {
val lastIndex = this.indexOfLast { weight-> weight != 0 }
// 모두 0인 경우 그냥 도로위가 빈 상태, 로직 특성상 도로위에는 항상 트럭이 있음. (선 삭제 후이동이 아닌 선 이동 후 삭제이기 때문에)
val needMoveCount = this.size - lastIndex - 1
Collections.rotate(this, needMoveCount) // 선두주자가 다리 끝에 도착 하여 마지막 자리로 이동.
// 다리 끝에 도착하여 이동된 트럭 무게 미리 계산
currentWeightOnBridge -= this.last
this.removeLast()
this.addLast(0)
moveCount += needMoveCount
}
}
}
// 위 forEach 분기가 끝나는 시점엔 맨 마지막 트럭이 다리위에 올려져 있는 상태이다.
// 따라서 길이만큼 이동이 필요하다.
return moveCount + bridge_length
}
}
fun main() {
// val answer = TrucksOnBridge().solution(2, 10, intArrayOf(7, 4, 5, 6))
// val answer = TrucksOnBridge().solution(100, 100, IntArray(10){10})
// val answer = TrucksOnBridge().solution(100, 100, intArrayOf(10))
val answer = TrucksOnBridge().solution(5, 5, intArrayOf(2,2,2,2,1,1,1,1,1))
println(answer)
}😂 풀이2 (오답)
import java.util.*
class Solution2 {
fun solution(bridge_length: Int, weight: Int, truck_weights: IntArray): Int {
var moveCount = 0
val bridgeLinkedList = LinkedList<Int>(List<Int>(bridge_length){0})
var index = 0
var currentWeightOnBridge = 0
while (index < truck_weights.size) {
// 다리 위에 트럭 넣기 with 이동
while(index < truck_weights.size && weight >= currentWeightOnBridge + truck_weights[index]) {
with(truck_weights) {
currentWeightOnBridge += this[index]
bridgeLinkedList.addFirst(this[index])
// Collections.rotate(bridgeLinkedList, 1)
bridgeLinkedList.pollLast()
// bridgeLinkedList.pollFirst()
index++
moveCount++
}
}
// 이동하기 to 다리 끝자리 until 다음 트럭 추가 무게 확보까지
if (index < truck_weights.size && weight < currentWeightOnBridge + truck_weights[index]) {
with(bridgeLinkedList) {
// 최선두 트럭 위치 구하기
val lastTruckIndex = this.indexOfLast { weight-> weight != 0 }
val distance = this.size - lastTruckIndex - 1
Collections.rotate(this, distance)
moveCount += distance
currentWeightOnBridge -= this.pollLast()
this.add(0)
}
}
}
// 다 넣었으면 이제 분기..
val lastTruckIndex = bridgeLinkedList.indexOfFirst { it != 0 }
if(lastTruckIndex == -1) println("세상에@@")
return moveCount + (bridgeLinkedList.size - lastTruckIndex)
}
}🔑 풀이3 (정답)
class Solution3 {
fun solution(bridge_length: Int, weight: Int, truck_weights: IntArray): Int {
var moveCount = 0
val bridgeLinkedList = LinkedList<Int>(List<Int>(bridge_length){0})
var index = 0
var currentWeightOnBridge = 0
while (index < truck_weights.size) {
// 다리 위에 트럭 넣기 with 이동
while(index < truck_weights.size && weight >= currentWeightOnBridge + truck_weights[index]) {
with(truck_weights) {
currentWeightOnBridge += this[index]
bridgeLinkedList.addFirst(this[index])
// rotate 방식이 아니기 때문에 마지막 원소가 0이 아닐 수 있음 , 이 경우 무게 제외
currentWeightOnBridge -= bridgeLinkedList.pollLast() // 0일 경우 알아서 영향 X
index++
moveCount++
}
}
// 이동하기 to 다리 끝자리 until 다음 트럭 추가 무게 확보까지
if (index < truck_weights.size && weight < currentWeightOnBridge + truck_weights[index]) {
with(bridgeLinkedList) {
// 최선두 트럭 위치 구하기
val lastTruckIndex = this.indexOfLast { weight-> weight != 0 }
val distance = this.size - lastTruckIndex - 1
Collections.rotate(this, distance)
// 최선두 트럭 다리 맨 끝으로 이동할 때까지 모든 트럭 같이 이동
moveCount += distance
currentWeightOnBridge -= this.pollLast()
this.addLast(0)
}
}
}
// 다 넣은 시점에 마지막 트럭은 다리 시작점에 있음. -> 길이만큼 추가
return moveCount + bridge_length
}
}
🔨 풀이4
⭐ 기존 풀이와 차이점
'roate' 없이 모든 루프의 케이스를 둘로 분기한다.
적재하면서 한칸 이동 vs 오로지 이동
이동이지만 뒤로 한칸 옮기는 행위이기 때문에 첫 칸을 추가하고
한 사이클 마다 맨 뒷칸은 무게를 반영하며 삭제한다 (pollLast())
⚠️ 풀이3보다 코드는 짧더라도 좋은 풀이는 아니다.
다리 길이 10,000 무게가 10, 000일때 트럭당 무게가 10000에 10000개면 10,000 * 10,000 == 1억번 이동한다.
=> Worst case - Time Complexity : O(N^2)
import java.util.*
class Solution {
fun solution(bridge_length: Int, weight: Int, truck_weights: IntArray): Int {
var index = 0
var currentWeightOnBridge = 0
var moveCount = 0
val bridgeQueue = LinkedList<Int>(List<Int>(bridge_length){0})
while (index < truck_weights.size) {
moveCount++
currentWeightOnBridge -= bridgeQueue.pollLast()
// 적재시에도 이동횟수 + 1 (시간 흐름)
if (weight >= currentWeightOnBridge + truck_weights[index]) {
bridgeQueue.addFirst(truck_weights[index])
currentWeightOnBridge += truck_weights[index++]
} else {
// 오로지 이동만
bridgeQueue.addFirst(0)
}
}
return moveCount + bridge_length
}
}
이놈도 저번 문제와 마찬가지로 테스트 케이스가 극단적인 케이스가 안나와서 그렇지..
