
Graph 개념
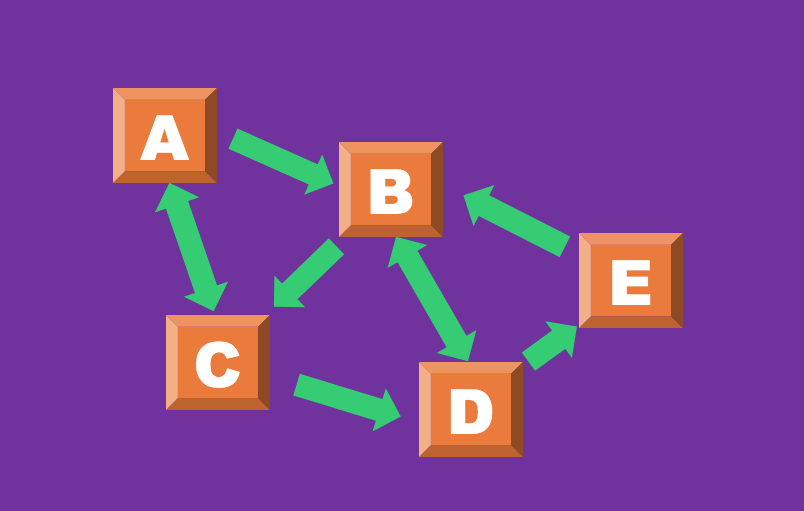
위의 사진은 그래프를 시각적으로 표현한 예시이다.
Graph란?🤔 🤔
여러 정점들이 간선들로 연결되어 묶여있는 자료구조이다.
그래프 복잡한 연결 구조망의 형태는 네트워크 망의 모델이다.
정점 Vertex: A, B, C, D, E
간선 Edge: 각 Vertex들의 연결점이다.
여기서 정점들 간의 간선들이 양방향과 단방향으로 나눠져 있는 특징을 볼 수있다.
이를 무향 그래프(양방향) 와 방향 그래프(단반향) 로 구분된다.
무향 그래프와 방향 그래프
(위의 사진을 예로 정리해서 진행하겠다.)
A 정점의 간선: A -> B || A <-> C
B 정점의 간선: B -> C || B <-> D
C 정점의 간선: C -> D || C <-> A
D 정점의 간선: D -> E || D <-> B
E 정점의 간선: E -> B
Graph 용어 정리
- 정점(vertex): 그래프 상의 위치를 갖고 있는 하나의 점 (vertex는 node와 뜻이 같음)
- 간선(edge): 각 위치를 갖고 있는 정점 간의 관계. 즉, 정점을 연결하는 선
- 인접 정점(adjacent vertex): 간선을 통해 직접 연결된 정점
- 정점의 차수(degree): 무향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (input)
- 진출 차수(out-degree): 방향 그래프에서 외부로 향하는 간선의 수 (output)
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
- 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
Graph 표현 방식
그래프를 표현하는 것에 두가지 방법이 있다.
인접 행렬(Adjacency Matrix)
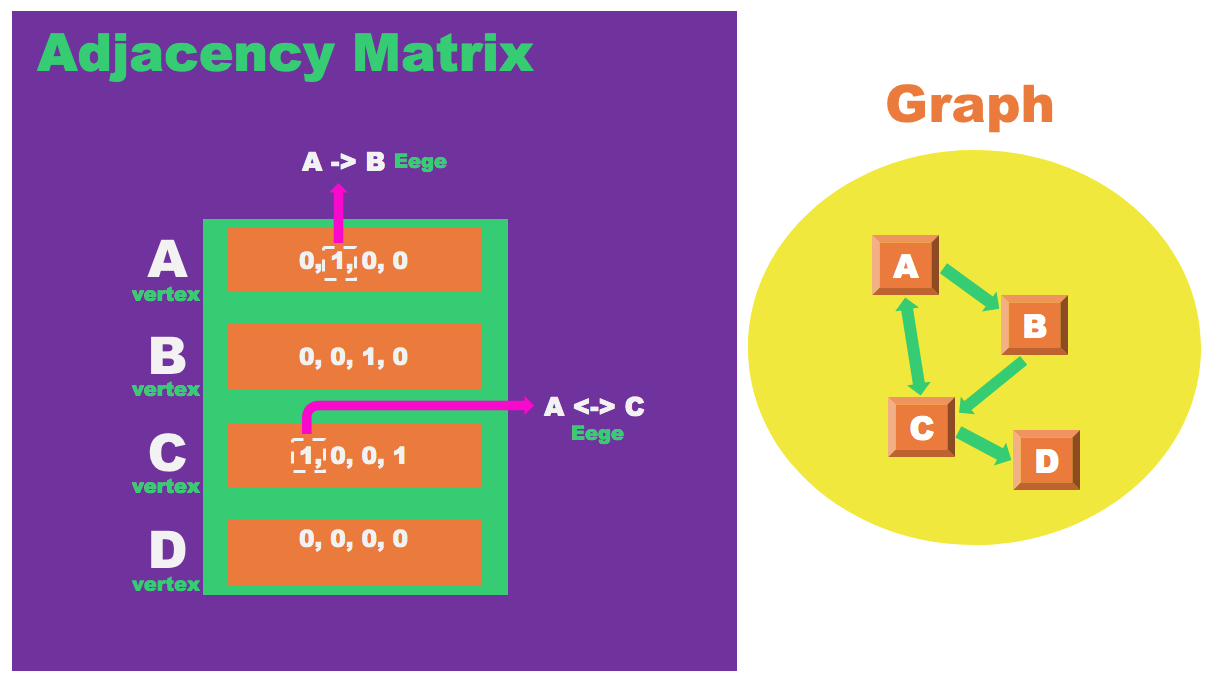
for(생성된 인접 행렬 매트릭스) {
if(해당 간선이 방향 그래프) {
matrix[i][j] = 1
} else 해당 간선이 무방향 그래프 {
matrix[i][j] = 1
matrix[j][i] = 1
}
}
많은 간선이 연결되어 있는 밀집 그래프(Dense Graph) 및 가장 빠른 경로(shortest path )에서
자주 응용한다.
-
장점
두 정점 간의 간선의 존재를 확인할 경우 1 혹은 0인지 확인만 하면 되므로 0(1) 상수 시간 복잡도에 유리하다. -
단점
인접 리스트와 달리 인접한 노드를 찾기 위해 모든 노드 간선을 순회해야 한다.
인접 리스트(Adjacency List)
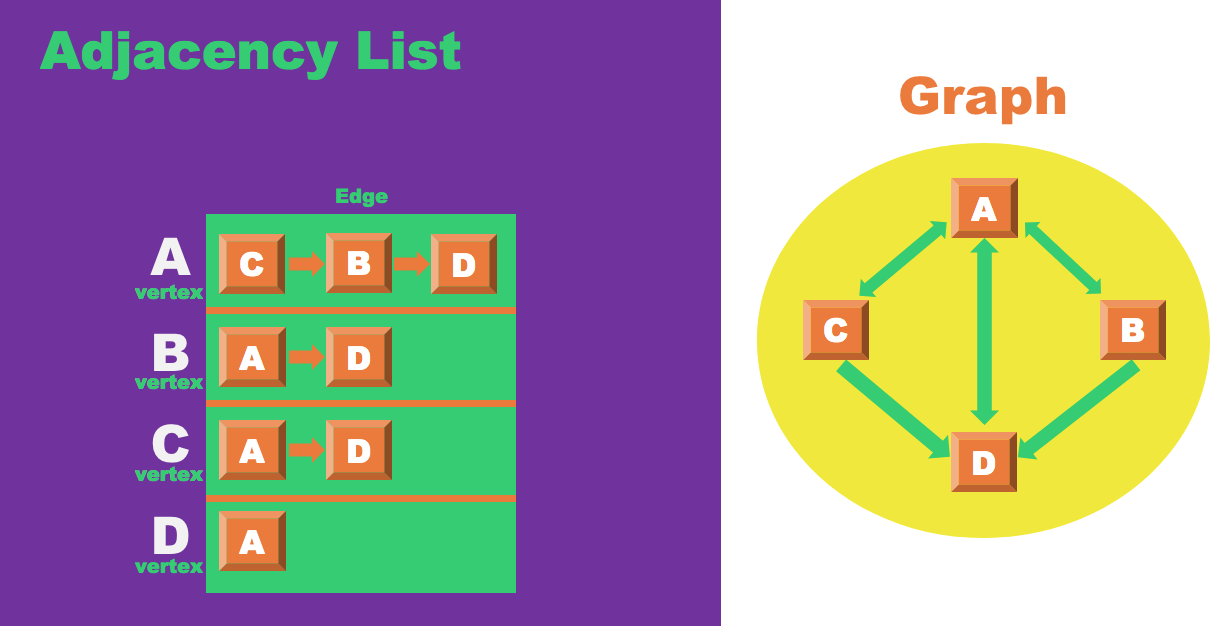
{ 0: [], 1: [], 2: [], ... 5: []}
for(생성된 obj 객체) {
객체에 배열 리스트 공간 넣기
obj[i] = []
}
0: [1]
1: [0]
2: [3]
3: [2]
4: [5]
for (간선을 통해 인접 리스트 추가하기) {
obj[edges[i][0]].push(edges[i][1]);
obj[edges[i][1]].push(edges[i][0]);
}
메모리를 효율적 사용이 필요할 경우 인접 리스트를 사용한다.
-
장점
원하는 노드에 인접한 노드들을 쉽게 찾을 수 있다. ex) 0: [1, 2, 3] 0번 노드에 1~3번 노드 간선이 존재 -
단점
노드 간의 연결 여부를 확인할 경우, 리스트를 순회하여 찾고자하는 노드 간선을 찾아야 하는데 이는 시간 복잡도가 따른다.
BFS, DFS
그래프 탐색은 하나의 정점을 통해 연결된 모든 정점들을 한 번씩 모두 방문하는 것이
목적으로 맞춰진 자료구조 철학이며 모든 정점들을 탐색하는데 두 가지 방법들이 있다.
지금부터
BFS,DFS에 대해 알아보자BFS(Breadth-First Search)
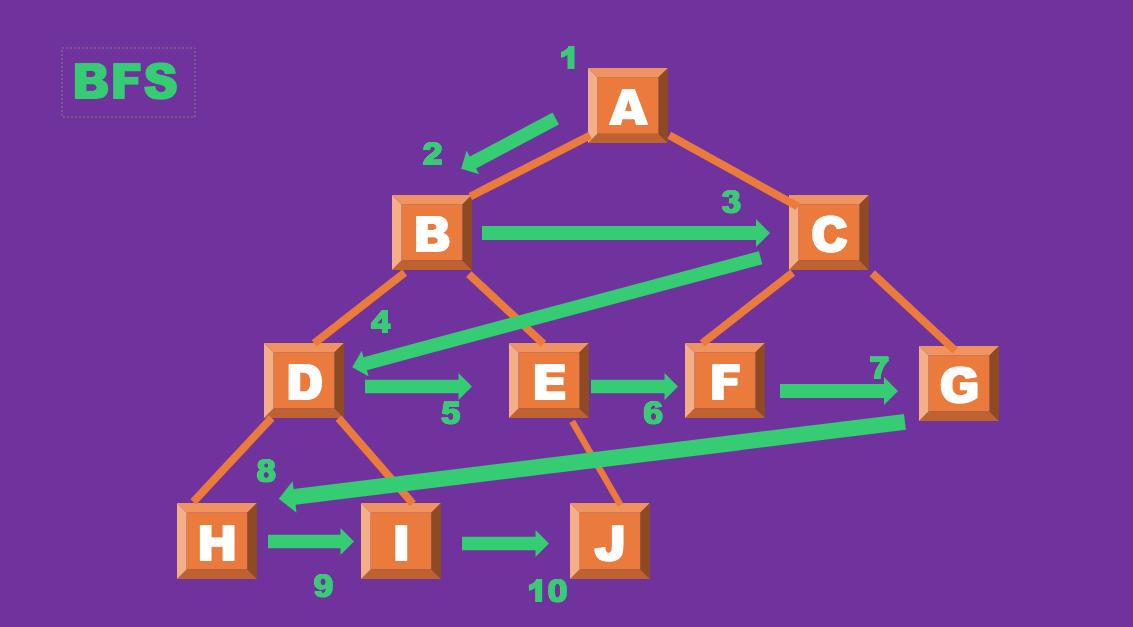
BFS는 너비 우선 탐색이라는 뜻으로 루트 노드에 시작해서 인접한 노드를 각각 먼저 탐색한다. -
사용하는 예: 두 노드 간 최단 경로 및 임의의 지정한 경로를 찾고자 할때 쓰인다.
ex) 수 많은 비행기 경로들 중 경유가 가장 짧은 최단 경로
DFS(Depth-First Search)
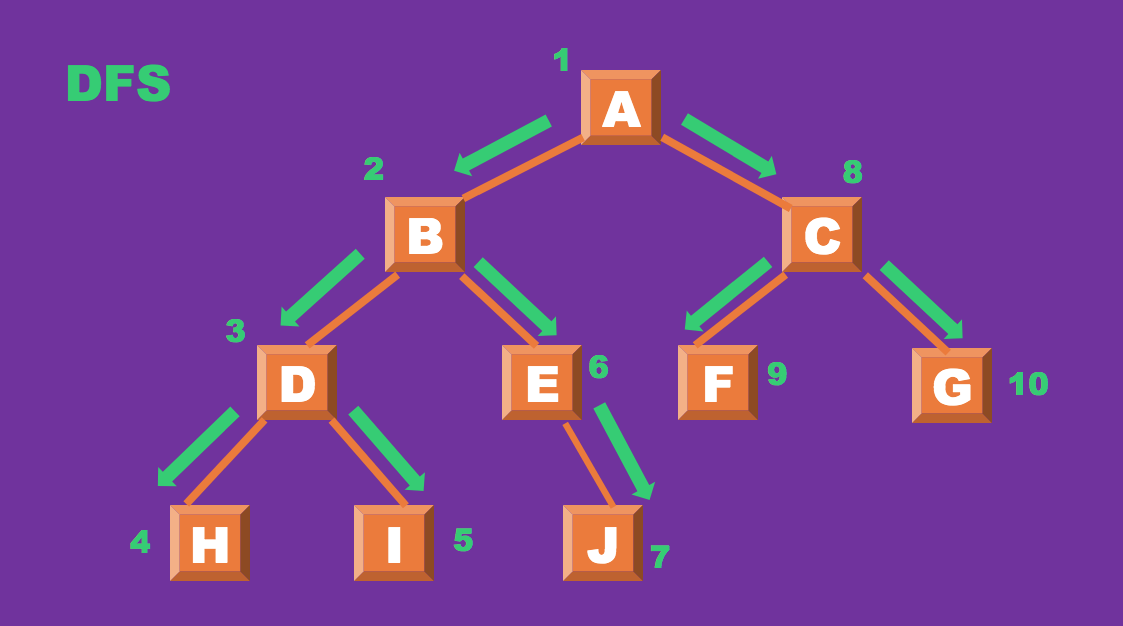
DFS는 깊이 우선 탐색이라는 뜻으로 루트 노드에 시작해서 다음 같은 레벨의 노드로 넘어가기 전
해당 분기를 완벽하게(=깊게) 탐색한다.
-
사용하는 예: 그래프 상의 모든 노드를 방문 하고자 할 경우 쓰인다.
(깊게 탐색하므로 재귀함수가 자주 활용)
ex) 내가 가고자 하는 목적지의 비행기 경로 탐색(경유 구간까지 세세하게 탐색)
