서론
우리FISA에서 15주 동안 코딩테스트 스터디를 했었다.
처음에는 기초 입출력도 잘 못했는데 하다보니 다행히 어느정도 코딩테스트 문제에 익숙해진 것 같다.
스터디에서 집중적으로 풀었던 DFS와 BFS문제에 대해서 정리하면 좋을 것 같아서 정리를 해봤다.
완전 탐색 문제
코딩테스트 문제를 보다보면 완전 탐색 문제 유형을 볼 수 있는데, 말 그대로 전부 탐색을 해보는 문제이다.
그런데 이때 탐색을 하는데 단순하게 반복문만을 사용해 가능한 모든 경우를 중복에 상관없이 탐색하다보면 분명히 시간초과 문제를 맞게 된다. 그래서 사용하게 되는 방식이 DFS와 BFS이다.
이제 이 둘에 대해서 알아보자.
DFS와 BFS
먼저 이 둘의 공통점을 알아보자.
DFS와 BFS는 앞서 언급했듯이 완전탐색 문제를 풀기 위해 사용하기 때문에 다음과 같은 공통점을 가진다.
방문처리
같은(Same) 경우를 중복해 탐색하는 것을 피하기 위해서
해당 위치를 탐색했음을 나타내는 자료구조 (배열, 리스트 등)을 사용한다.
방문 처리 라는 것을 하는데 특정 위치를 방문했을 때 배열이나 리스트 데이터에 현재 위치를 탐색했음을 표시해 주는 것이다.
이로써 방문 처리를 했는지 확인하면 다음에 같은 경우를 한 번 더 탐색해 시간을 낭비하는 일이 없어진다.
이 데이터를 새로 만들 필요 없이 문제에서 주어진 데이터를 가져다 수정해서 사용하기도 한다. (미로 탐색의 maze 배열 등)
같은 경우를 한 번 더 탐색한다는 것이 안 와닿는다면, 갈림길이 나뉘어도 어차피 이후의 경로가 똑같은 외길 경로로 다시 합쳐지는 경우를 생각해보면 된다.
위
_______
/ \
---- ===== 오른쪽
\_______/
아래오른쪽 길로 가기 위해서는 윗 길에서 오는 방법, 아랫길에서 오는 방법이 있다.
만약 먼저 윗길을 통해 오른쪽 길 (====)을 이미 탐색했다면, 이를 기억해 두고 아랫길을 통해왔을 때 오른쪽 길을 더이상 탐색하지 않는다.
그런데 탐색을 하기 위해서는 현재 위치에서 다음에 방문할 곳을 기록해두는 것도 필요하다.
큐(qeue)와 스택(stack)
등산을 해본 경험이 있다면, 산에서 이정표를 본 기억이 있을지도 모른다. 한 번 떠올려보자.
등산을 예로 드는 이유는 (홍대입구역이 도착지면 2호선인지, 5호선인지, 공항철도인지 몇 번 출구인지 등과 달리) 도착지가 단 하나의 지점(정상 봉우리)으로 정해져있어 실제 예로 들기 좋다고 생각되었다.
어떤 산을 등산하는것에 대해, 정상으로 가는 갈림길이 A, B 두 방향으로 나 있어서
등반 경로가 A로 갔을 때 다음 경로, B로 갔을 때 다음 경로로 나뉜다고 하자.

만약 당신이 이 산의 🧙♂️산신령이 되기위해서는 이 산의 정상으로 가는 모든 길을 알아야 해서 A쪽으로 갔을 때와 B쪽으로 갔을 때 모두 올라가봐야 한다고 한다.
(산신령이 되기 싫다고요? 그냥 봐주시죠. 누군가는 되고싶다잖아요.)

A를 먼저 갈지, B를 먼저 갈지는 상관없다. 산속에 존재하는 모든 경로를 보는것이 중요하다.
그래서 둘 중 아무 길인 A길을 선택해 먼저 가보기로 한다.
선택되지 않은 다른 길 B는 A라는 길을 갔을 때의 모든 경로를 확인한 후에 잊지 않고 가보도록 기억🚩해둘 필요가 있다.

그리고 A길로 출발 한 이후에도, 또 갈림길이 a, b로 나뉘고 a를 먼저 가보기로 했다면 b를 기억해 두어야한다.
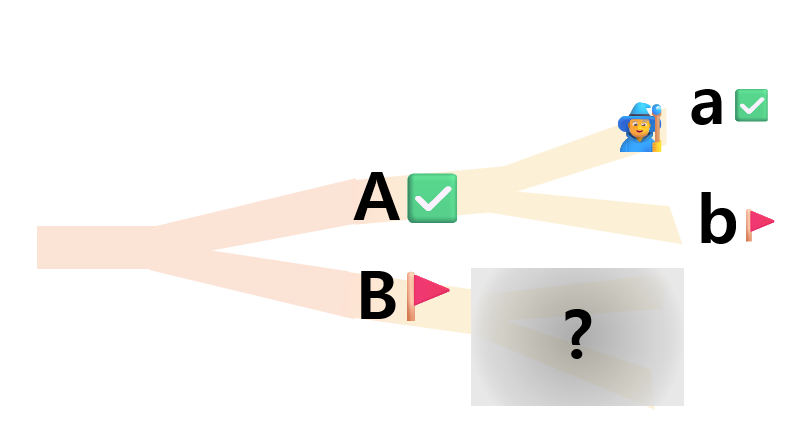
이제 A길로 가고 a길로 가고....를 반복하고 정상에 도착했다면, 당신은...?
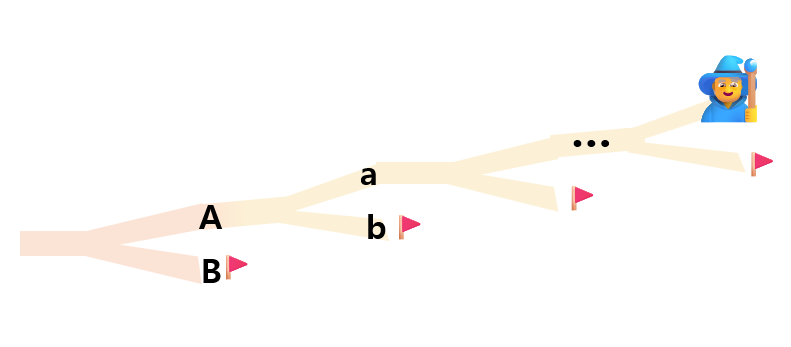
아직 산신령의 자격이 없다.😅
기억해두었던 B길, b길... 또한 모두 확인해봐야 한다.
BFS와 DFS는 이렇게 "방문해야 할 곳🚩"을 각각 '큐'와 '스택' 자료형을 통해 기억한다.
모든 경우를 탐색하기 위해 갈림길이 나타나는 곳까지 다시 산을 처음부터 올라 이동할 필요 없이 큐나 스택에 기억해둔 갈림길로 순간이동하면 모든 길을 빠르게 탐색 할 수 있다.
그런데 큐와 스택은 각각 선입 선출 vs 후입 선출로 빼는 순서가 다르다.
산신령의 등산으로 설명하자면, A,a를 먼저 방문하기로 했을 때 B와 b를 가는 순서는
큐를 사용하면 A로 갔을 때 발견했던 B를 먼저 탐색하고 a로 갔을 때 발견했던 b를 나중에 탐색하고,
스택을 사용하면 a로 갔을 때 발견한 b를 먼저 탐색하고 처음 A로 갔을 때 발견한 B를 나중에 탐색하는 것이다.
이 자료구조의 선택으로 탐색 순서 가 달라지는데, 이게 바로 DFS와 BFS의 차이 가 된다.
DFS
DFS는 깊이 우선 탐색(Depth First Search)로 보통 재귀함수() 를 통해 구현한다.
함수의 호출은 콜 스택을 이용하기 때문이다.
콜 스택이란 ?
콜 스택(call stack)이란 컴퓨터 프로그램에서 현재 실행 중인 서브루틴에 관한 정보를 저장하는 스택 자료구조이다.
라고 위키백과에서 한 마디로 정리했는데, '용어'는 어려우니까 예시를 통해 풀이해보자.
-
어떤 프로그램에서 main() 함수가 호출되어 프로그램이 시작되었다.
-
main()함수에서 어떤 함수func()를 호출했으면,
func()함수에 대한 정보를 콜스택에 추가한다. -
그리고 main()함수에서 호출된
func()함수가puckpuck()함수를 호출했다면
puckpuck() 함수에 대한 정보를 콜스택에 추가한다. -
puckpuck()함수가 할 일을 마치고 값이 반환되면 반환된 값을 어디로 전달하는지는 콜스택의 puckpuck() 정보를 pop한 뒤 콜스택에 남아있는 함수 정보를 확인하면 된다. 그려면 fucn() 함수가 puckpuck() 함수를 호출했다는 것을 알 수 있고, 반환값을 fucn()함수에 전달해줄 수 있게 된다. -
물론 main() 함수도 함수이기 때문에 콜스택에 저장되는데, 콜스택의 main() 함수의 유무가 프로그램 실행의 종료 여부와 같다.
(언어의 종류 및 구현에 따라 동작이 다를 수 있음)
함수의 반환값을 스택에 저장해둔 다른 함수에게 전달해준다는 것이 그 전 예시에 갈림길에서 선택하지 않은 길로 순간이동 해 돌아가는 것과 유사해 보인다!
DFS 코드 구현
이쯤에서 DFS의 미로 탈출 구현 코드를 살펴보자.
가독성을 위해 Python 코드로 작성한다.
# 당신을 위해 위 미로를 준비해 봤어요. 가운데의 복잡한 갈림길이 핵심이죠.
# 맨 아래 2에 오면 도착한 것으로 여길게요.
maze = [[1, 0, 0],
[1, 1, 1],
[1, 1, 0],
[1, 1, 0],
[0, 2, 0]]
# 방문 순서 기록
visit = [[0]*3 for i in range(5)]
flag = False
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
count = 0
def dfs(x, y):
global visit #dfs함수 바깥에서 활용하기 위해 전역변수 사용
global flag
global count
count +=1
visit[y][x] = count
for i in range(4):
nx = x+dx[i]
ny = y+dy[i]
if(nx<0 or ny<0 or nx>2 or ny>4): continue
if(maze[ny][nx] == 2):
count+=1
visit[ny][nx] = count
flag = True
return print(f"축하해요! {count} 번째에 탈출했어요!")
if(visit[ny][nx] == 0 and maze[ny][nx]!=0):
dfs(nx, ny)
if __name__ == "__main__":
flag = False
dfs(0, 0) # 가장 좌측 상단의 1에서부터 미로를 탐색해요.
if flag == False:
print("안축하해요! 당신은 미로에 스며들었어요!")
for i in visit:
print(i)
출력 :
축하해요! 9 번째에 탈출했어요! [1, 0, 0] [2, 7, 8] [3, 6, 0] [4, 5, 0] [0, 9, 0]
미로에서 탐색 가능한 모든 장소를 탐색하고 탈출 경로를 찾았다.
그런데 '9번째'에서야 탈출한 것에 주목해보자.
방문 순서를 나타낸 visit의 출력 결과를 보면 1,2,3,4,5 까지는 잘 가다가..
도착점을 코 앞에 두고 과감한 유턴...! 을 통해 8번째 방문에서 막다른 길을 확인하고 나서야 도착점을 확인한다.
즉, DFS에서는 미로 탈출은 할 수는 있지만, 탈출했을 때 완성된 출발점에서부터 도착점까지의 경로는 이론적으로 가능한 최단 이동 경로임을 보장하지 않는다.
BFS
BFS는 너비 우선 탐색 (Breadth-First Search)로 보통 큐와 반복문을 통해 구현한다.
BFS 코드 구현
from collections import deque
# 당신을 위한 미로를 그대로 가지고 있었어요
maze = [[1, 0, 0],
[1, 1, 1],
[1, 1, 0],
[1, 1, 0],
[0, 2, 0]]
visit = [[0]*3 for i in range(5)]
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
def bfs(start_x, start_y):
queue = deque([(start_x, start_y)])
visit[start_y][start_x] = 1 # 시작 위치 방문 처리
while queue:
x, y = queue.popleft() # deque 사용 : O(1) 시간 복잡도로 요소 제거 (그냥 리스트 자료형의 pop(0) 사용시 O(n))
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or ny < 0 or nx > 2 or ny > 4: continue
if maze[ny][nx] == 2:
visit[ny][nx] = visit[y][x] + 1
return print(f"축하해요! {visit[ny][nx]} 번째에 탈출했어요!")
if visit[ny][nx] == 0 and maze[ny][nx] != 0:
visit[ny][nx] = visit[y][x] + 1
queue.append((nx, ny))
return print("안축하해요! 당신은 미로에 스며들었어요!")
if __name__ == "__main__":
bfs(0, 0)
for i in visit:
print(i)
출력 :
축하해요! 6 번째에 탈출했어요! [1, 0, 0] [2, 3, 4] [3, 4, 0] [4, 5, 0] [0, 6, 0]
세로로 이어지는 1, 2 탐색 이후, 갈림길이 나누어질 때 물이 퍼지듯이 3,3 4,4,4 순서로 탐색을 하고 6번째만에 탈출을 할 수 있음을 알 수 있다.
실제로 코드실행 단계에서 방문 순서는 dx와 dy 탐색 따라 같은 방문 순서를 3번째((x,y): (0,2), (1,1)), 4번째((0,3),(1,2),(2,1))를 방문하는 단계가 추가로 있긴 할것이다.
(완전 탐색이므로 최단 경로를 알려줄 뿐, 탐색 자체를 최단으로 하진 않는다.)
마무리
- DFS와 BFS에 대해 알아보고 길찾기 문제에 활용하는 방법을 살펴보았다.
- 문제 해결을 위해 알고리즘을 선택할 때, 문제를 외워서 이 문제엔 이 알고리즘이지! 라고 푸는게 아니라 각 알고리즘의 특성을 고려해보고 선택하도록 해야겠다.
- 최단 거리문제를 풀기 위해서는 BFS를 사용해야함을 알겠는데, DFS의 콜스택에서 사용하는 메모리와 BFS의 큐에서 사용하는 메모리 사용에 대해 좀 더 알아봐야겠다.
문제를 풀면 이해 했다고 생각했는데 머릿속에 있는 내용을 끄집어내보니 생각보다 얼기설기 정리되어있지 않은 부분이 많이 보였다. 앞으로도 글을 쓰면서 혹은 다른사람에게 설명하면서 내 생각이 맞는지 확인하는 습관을 가지자. 💖🔥

