[알고리즘]Greedy(탐욕법) 알고리즘

Ming·2022년 1월 17일
알고리즘
0

알고리즘

목록 보기
2/10

탐욕법(Greedy) 알고리즘

탐욕법 알고리즘은 동적 프로그래밍 사용 시 지나치게 많은 일을 한다는 것에서 착안하여 고안되었다. 탐욕법 알고리즘이란 현재 상황에서 지금 이 순간 최적인 답을 선택하여 적합한 결과를 도출하는 알고리즘이다. 현재 상황에서 가장 좋은 선택이 최종적인 결과에 대한 최적해를 보장해주는 것이 아니다.

특징

  • 현재 상황에서 가장 좋은 것만 선택해도 문제가 해결되는지 파악한 후, 적용해야한다
  • 동적 계획법과 상호보완적이다.

    그리디 알고리즘 문제가 나왔을 때 "가장 큰 순서대로", "가장 작은 순서대로"라는 기준을 제시해준다.
    정렬문제와 짝을 이루어 출제된다.

장점

  • 계산 속도가 빠르다
  • 효율적으로 최적해를 찾을 수 있다

탐욕 알고리즘 문제를 해결하는 방법

  1. 현재 상태에서 최적의 답을 찾는다
  2. 선택한 최적의 답이 문제의 조건에 맞는지 확인한다
  3. 문제가 해결되었는지 확인하고, 해결 되지 않는다면 1번으로 돌아가 위의 과정을 반복한다

조건

  • 탐욕스런 선택 조건
    선택으로 인해 전체 문제의 최적해를 반드시 도출할 수 있어야 한다는 조건
  • 최적 부분 구조 조건
    문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적의 해결 방법이다라는 조건

문제

  • 활동 선택 문제 백준 1931

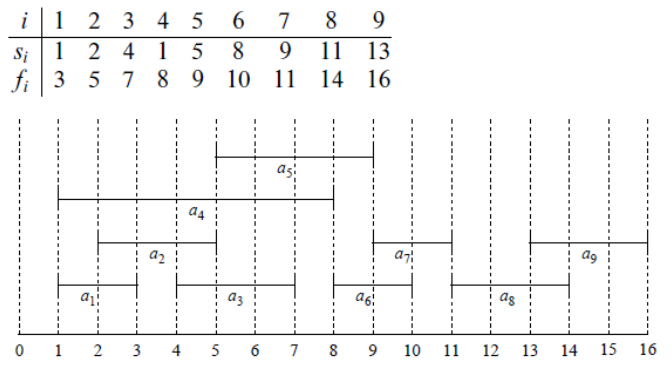
    활동 선택 문제는 한 강의실에서 여러개의 수업을 하려고 할 때 한번에 가장 많은 수업을 할 수 있는 경우를 고르는 것이다.
    Si는 수업 시작 시간 Fi는 수업 종료시간이다. 타임 테이블을 보면 a1이 가장 빨리 끝나므로 선택을 하고 그 다음 빨리 끝나는 수업은 a3이므로 선택을 한다. 반복하다보면 정답은 [a1, a3, a6, a8], [a1, a3, a7, a8]이다.

  • 파이썬 구현


timetable = [[1, 3], [2, 5], [4, 7], [1, 8], [5, 9], [8, 10], [9, 11], [11, 14], [13, 16]]

timetable.sort(key=lambda x:(x[1], x[0]))
cnt = 1
classes = []
classes.append(1)
end_time = timetable[0][1]
for i in range(1, len(timetable)) :
  if timetable[i][0] >= end_time :
    cnt+=1
    end_time=timetable[i][1]
    classes.append(i+1)
print(cnt)
print(classes)
  • 자바 구현
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class BOJ_1931 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n=sc.nextInt();
        int[][] timetables=new int[n][2];
        for(int i=0; i<n; i++){
            timetables[i][0]=sc.nextInt();
            timetables[i][1]=sc.nextInt();
        }

        Arrays.sort(timetables, new Comparator<int[]>(){
            @Override
            public int compare(int[] o1, int[] o2){
                if(o1[1]==o2[1]){ //종료시간이 같을 경우 시작 시간이 빠른 순
                    return o1[0]-o2[0];
                }else{
                    return o1[1]-o2[1];
                }
            }
        });
        int ans=1;
        int end_time=timetables[0][1];
        for(int i=1; i<n; i++){
            if(end_time<=timetables[i][0]){
                end_time=timetables[i][1];
                ans+=1;
            }
        }
        System.out.println(ans);
    }
}

💡 거스름돈 문제

당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한개 존재합니다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러주어야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.

  • 가장 큰 단위의 돈부터 생각하자
  • 최소 개수를 구하는 문제이므로 가장 큰 단위부터 거슬러주고 나머지를 그 다음 단위의 화폐로 거슬러 주는 것
def solution(돈):
	answer=0
	arr = [500, 100, 50, 10]
	remain = money
	for coin in arr:
		answer += remain // coin		
		remain %= coin
	
	return answer

💡 부분 배낭 문제 Fractional Knapsack Prob

무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣음
각 물건은 무게와 가치로 표현
➡️ 물건은 쪼갤 수 있음으로 Fractional 이라 함
(쪼갤 수 없는 배낭 문제는 0/1 Knapsack Problem(다이나믹 프로그래밍))

datas=[(10,10), ...]
def get_max_value(datas,capacity):
	datas = sorted(datas,key=lambdㄱa x:x[1]/x[0],reverse=True)
    	# 어떤 기준으로 정렬할 것인지 선택하는 것이 최적 선택의 시작
    total=0
    details=list()
    
    for data in datas:
    	if capacity - data[0]>=0: # 통째로 넣기
        	capacity-=data[0]
            total+=data[1]
            details.append(data[0],data[1],1])
        else: # 쪼개서 넣기
        	fraction = capacity/data[0]
            tota+=data[1]*fraction
            details.append([data[0],data[1],fraction])
            break # 더 이상 계산 안해도 됨
        return total,details

➡️ 지금 순간에 최적을 찾기. 그 순간에 가장 가치가 높은 것을 고르는 것. 하지만 그 순간의 최적이기에 완벽히 최적일 수는 없다.

💡 Kruskal Algorithm

가중치를 간선에 할당한 그래프인 네트워크의 모든 정점을 최소 비용으로 연결하는 최적 해답 구하는 것
MST(최소 비용 신장 트리)가 1) 최소 비용의 간선으로 구성됨 2) 사이클을 포함하지 않음의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다.

간선을 거리가 짧은 순서대로 포함시키기

  • 모든 노드를 최대한 적은 비용으로 연결만
  • 모든 간선 정보를 가중치를 기준으로 오름차순으로 정렬 후 비용이 적은 간선부터 차근차근 그래프에 포함시키면 된다.

동작

  • 간선 선택을 기반으로 함
  • 이전 단계와 상관없이 무조건 최소 간선만을 선택

주의

  • 선택된 간선들 집합에 다음 간선을 추가시 사이클 생성 여부 확인 체크
    ➡️ union-find 알고리즘 이용 : 추가하고자 하는 간선이 양끝 정점이 같은 집합에 속하는지 검사

사실상 정렬 알고리즘과 union-find 알고리즘의 합으로 볼 수 있다.

코드

#1

graph=[(1,2,13),....] #(정점1, 정점2, 가중치)
graph.sort(key=lambda x:x[2])

mst=[]
n=len(graph)
p=[0] # 상호 배타적 집합 <<??

for i in range(1,n+1):
	p.append(i) # 각 정점 자신이 집합의 대표
def find(u):
    if u!=p[u]:
    	p[u]=find(p[u]) # 경로 압축
    return p[u]
def union(u,v):
    root1=find(u)
    root2=find(v)
    p[root2]=root1 # 임의로 root2가 root1의 부모

tree_edges=0 # 간선 개수
mst_cost=0 # 가중치 합
while True:
    if tree_edges==n-1:break
    u,v,wt = graph.pop(0)
    if find(u)!=find(v): # u와 v가 서로 다른 집합에 속해 있으면
    union(u,v)
    mst.append((u,v))
    mst_cost+=wt
    tree_edges+=1

#2

# 특정 원소가 속한 집합을 찾기
def find(parent, x):
    if parent[x] == x:
        return x
    parent[x] = find(parent, parent[x])
    return parent[x]


# 두 원소가 속한 집합을 합치기 (간선 연결한다고 생각!)
def union(parent, a, b):
    rootA = find(parent, a)
    rootB = find(parent, b)

    if rootA < rootB:
        parent[rootB] = rootA
    else:
        parent[rootA] = rootB


import sys

input = sys.stdin.readline
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1)

edges = []
result = 0

# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
    parent[i] = i

# 모든 간선에 대한 정보를 입력받기
for _ in range(e):
    a, b, cost = map(int, input().split())
    # 비용순으로 오름차순 정렬하기 위해 튜플의 첫 번째 원소를 비용으로 설정
    edges.append((cost, a, b))

edges.sort()

for edge in edges:
    cost, a, b = edge
    # 사이클이 발생하지 않는 경우에만 집합에 포함(=연결한다.)
    if find(parent, a) != find(parent, b):
        union(parent, a, b)
        result += cost

print(result)

# sample input
# 7 9
# 1 2 29
# 1 6 75
# 2 3 35
# 2 6 34
# 3 4 7
# 4 6 23
# 4 7 13
# 5 6 53
# 6 7 25

시간 복잡도

profile
Ming
이전 포스트

[알고리즘]스택, 큐, 우선순위 큐

다음 포스트

[알고리즘]동적 계획법(Dynamic Programming)

0개의 댓글