Batch Normalization

*본 게시글은 블로그 게시글 JINSOL KIM Computer Vision for Autonomous Driving '배치 정규화(Batch Normalization)' 자료를 참고한 점임을 알립니다.

Batch Normalization

1. 배치 정규화 (Batch Normalization)

Batch Normalization(BN)은 딥러닝 모델의 학습 속도를 높이고, 안정성을 증가시키는 정규화 기법입니다. 이는 각 미니배치 내에서 데이터의 평균과 분산을 이용하여 입력을 정규화한 후, 스케일링 파라미터$γ$와 시프트 파라미터 $β$를 적용하여 학습을 진행합니다. BN은 특히 내부 공변량 이동(Internal Covariant Shift) 문제를 해결하며 학습 속도를 크게 개선합니다.

2. 내부 공변량 변화 (Internal Covariant Shift)

Internal Covariant Shift는 딥러닝에서 학습 중 각 레이어의 입력 데이터 분포가 변하는 문제를 말합니다. 네트워크가 학습하면서, 각 레이어가 이전 레이어에서 받은 입력의 통계적 특성이 지속적으로 변하면, 다음 레이어는 그에 맞게 계속 적응해야 합니다. 이로 인해 학습이 불안정해지고, 속도가 느려질 수 있습니다. 쉽게 말해, 각 레이어가 "적응해야 할 환경"이 계속 변하는 상황이 발생하는 것이 Internal Covariant Shift입니다.

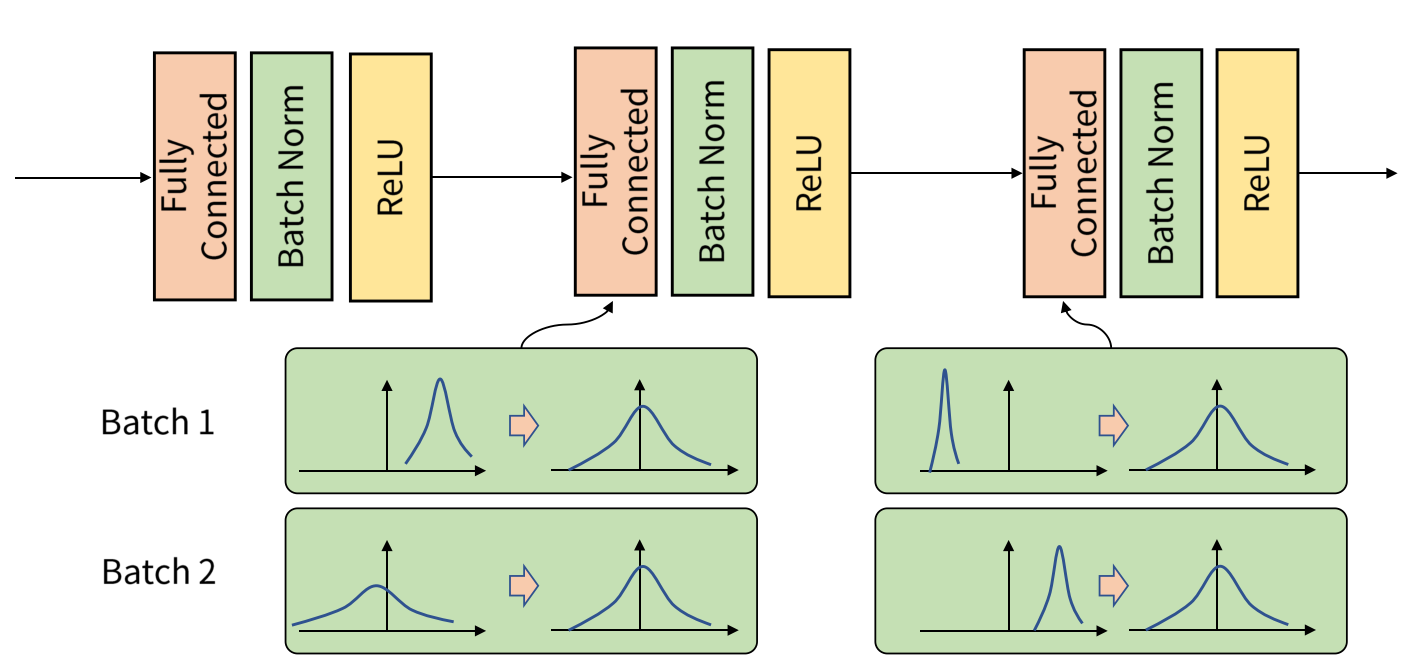
한 레이어가 출력한 결과가 다음 레이어로 전달될 때, 그 분포가 바뀌면 다음 레이어는 새로운 분포에 적응해야 합니다. 이 과정에서 학습이 느려지거나 불안정해집니다. 이는 특히 심층 신경망(Deep Neural Networks)에서 문제가 되며, 학습 과정에서의 비효율성을 초래합니다.

이 문제는 딥러닝 네트워크의 깊이가 깊어질수록 더 심각해집니다. 레이어가 많아질수록 입력 데이터의 분포 변화가 누적되며, 이러한 변화는 네트워크가 학습하는 동안 적절한 학습 속도를 유지하기 어렵게 만듭니다.

Batch Normalization은 Internal Covariant Shift 문제를 완화하기 위한 해결책입니다. 각 레이어의 입력 데이터를 정규화하여 평균과 분산을 일정하게 유지함으로써 레이어 간의 분포 변화 문제를 줄이고, 학습을 더 안정적이고 빠르게 진행할 수 있게 합니다.

3. 동작 원리

(1) 배치별 평균 구하기

미니배치에서 각 데이터의 평균 $μ_{batch}$를 계산합니다.

(2) 배치별 분산 구하기

각 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 분산 $σ_{batch}^2$는 다음과 같이 구합니다:

(3) 데이터 정규화하기

각 데이터 $𝑥_𝑖$에서 평균 $μ_{batch}$를 빼고, 분산 $σ_{batch}^2$의 제곱근을 나누어 정규화합니다. 데이터 $x_i$를 평균 0, 분산 1인 상태로 정규화합니다. 즉, 입력 데이터의 각 배치에 대해 평균을 0으로, 분산을 1로 맞추게 되는 것이죠. $ϵ$은 숫자 0으로 나누는 문제를 방지하기 위한 작은 값입니다.

(4) 스케일 및 시프트 적용 정규화된 데이터에 학습 가능한 파라미터 $γ$와 $β$를 적용하여 조정합니다.

4. 학습 단계 (Training Phase) vs 추론 단계 (Inference Phase)

Batch Normalization은 학습 단계와 추론 단계에서 다르게 작동합니다. 여기서 두 단계의 차이점을 수식과 함께 살펴보겠습니다.

(1) 학습 단계

학습 단계에서는 매번 배치마다 입력 데이터의 평균과 분산을 계산하고 이를 이용해 정규화합니다. 각 배치에서 계산한 배치 평균 $μ_{batch}$와 배치 분산 $σ_{batch}$을 사용하여 입력을 정규화합니다.

여기서 $γ$와 $β$는 학습 가능한 파라미터로, 각 배치에서 계산된 값에 대해 조정하는 역할을 합니다. 매 배치마다 계산된$μ_{batch}$와 $σ_{batch}$를 사용하여 정규화하므로, 학습 중 데이터 분포가 변해도 각 배치별로 즉각적으로 적용할 수 있습니다.

(2) 추론 단계

추론 단계에서는 학습 단계에서 배치 단위로 구했던 평균과 분산을 매번 계산할 수 없습니다. 대신 학습 단계에서 계산한 이동 평균(Moving Average)

[2-1] 이동 평균

일정한 구간의 데이터 평균을 구하는 방식입니다. 학습 중 최근 N개의 배치에 대한 평균을 구해 추론에 사용합니다. 단순 평균이며, 최근 데이터와 이전 데이터를 동일한 중요도로 취급합니다.

혹은 지수 평균(Exponential Average)을

[2-2] 지수 평균

더 최근의 배치에 가중치를 더 주는 방식입니다. 최근 배치의 값일수록 가중치가 커지고, 과거 배치의 값은 빠르게 반영되지 않게 됩니다. 가중치 $α$는 최근 배치의 중요도를 결정합니다.

을 사용합니다. 이와 같이 이동 평균 혹은 지수 평균에 따른 $\mu_{BN}$을 활용합니다.

여기서 $μ_{BN}$과 $σ_{BN}^2$는 학습 중에 계산된 고정된 평균과 분산입니다. $ϵ$은 0으로 나누는 문제를 피하기 위해 추가된 작은 상수입니다.

학습에서 사용된 배치별 통계값 대신 학습 중 계산한 이동 평균 혹은 지수 평균을 사용하여 데이터를 정규화합니다.이는 추론 단계에서 일관성을 유지하고, 각 배치마다 분포가 달라지는 문제를 방지하기 위해서입니다.

5. 장점과 단점

장점

• 학습 안정성 증가: BN은 각 레이어의 입력을 정규화하여, 학습이 더 안정적으로 진행될 수 있도록 돕습니다.
• 학습 속도 향상: BN은 내부 공변량 이동 문제를 완화하여, 학습 속도가 크게 향상됩니다. 특히 높은 학습률에서도 학습이 잘 이루어지게 합니다.
• 초기화 의존성 감소: BN을 사용하면 모델의 가중치 초기화에 민감하지 않게 되며, 다양한 초기 설정에서도 성능이 개선됩니다.

단점

• 작은 배치에서의 한계: BN은 미니배치의 크기에 의존하기 때문에, 배치 크기가 너무 작으면 BN이 제대로 동작하지 않을 수 있습니다.
• 순환 신경망(RNN)에 부적합: 시계열 데이터를 다루는 RNN에서는 BN이 성능을 저하시킬 수 있으며, 이를 해결하기 위해 Layer Normalization 같은 다른 기법이 필요합니다.

참고 자료

• JINSOL KIM Computer Vision for Autonomous Driving '배치 정규화(Batch Normalization)'