컴퓨터 아이콘 제작자: Freepik - Flaticon
문제 설명
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.
각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.
제한 사항
numbers는 길이 1 이상 7 이하인 문자열입니다.
numbers는 0~9까지 숫자만으로 이루어져 있습니다.
"013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.
입출력 예
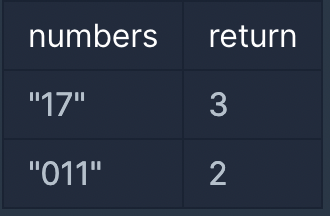
입출력 예 설명
입출력 예 #1
[1, 7]으로는 소수 [7, 17, 71]를 만들 수 있습니다.
입출력 예 #2
[0, 1, 1]으로는 소수 [11, 101]를 만들 수 있습니다.
11과 011은 같은 숫자로 취급합니다.
Solution 1(순열을 사용한 풀이)
from itertools import permutations
def solution(numbers):
prime_set = set()
# 모든 숫자 조합을 만든다.
for i in range(len(numbers)):
# numbers란 스트링값을 리스트로 받으면 각각 따로 분리되어 보여진다. 순열은 순서를 고려하기 때문에 파이썬에서 제공하는 permutations를 사용하면 편하다. i + 1 은 조합의 개수를 말한다.
per_list = permutations(list(numbers), i + 1)
# 맵이라는 함수를 사용하여 하나로 엮어준다음 per_list가 가지고있는 조합을 "".join한다음(str.join) int형으로 변환
per_list = (map(int, map("".join, per_list)))
# |= eq)x = x | y, 중복을 제거하기 위해 집합인 set를 사용
prime_set |=set(per_list)
# 소수가 아닌 수 0과 1을 prime_set에서 제외
prime_set -= set(range(0,2))
# 에라토스테네스의 체를 사용(prime_set의 최댓값에 루트를 씌우고, range의 두번째 인자로 사용하기 위해서 1을 더해준다음 int형으로 형변환(캐스팅)을 해준다.)
lim = int(max(prime_set) ** 0.5) + 1
for i in range(2, lim):
# i*2 부터 max(prime_set)까지 i 간격 만큼 건너뛰면서
prime_set -= set(range(i*2, max(prime_set) +1, i))
return len(prime_set)

