1. 삽입 정렬 (Insertion Sort)
- 거의 정렬된 상태의 자료라면, 삽입 정렬이 가장 좋은 퍼포먼스를 보일 수도 있다!
- 분할 정복 정렬 알고리즘을 개선할 때 자주 채용되곤 합니다. 작은 단위의 자료를 정렬할 때 효율적이기 때문입니다
- Best 퍼포먼스: 이미 정렬된 자료
- Worst 퍼포먼스 : 역으로 정렬된 자료
2. 선택 정렬 (Selection Sort)
- 쓰지 맙시다^^
3. 버블 정렬 (Bubble Sort)
- 이것도 쓰지 맙시다^^
4. 셸 정렬 (Shell Sort)
- 삽입 정렬의 확장판이라고 할 수 있다 (삽입 정렬에 gap 개념을 도입)
- 삽입 정렬의 단점은 삽입되어야 하는 지점이 현재의 지점과 멀면, 이동 횟수가 많아진다는 것입니다
셸 정렬은 이러한 단점을 gap을 통해 해결하는 정렬 알고리즘입니다
5. 퀵 정렬 (Quick Sort)
-
분할 정복(divide and conquer) 알고리즘입니다
-
피벗(pivot)을 어떻게 선택하냐에 따라 정렬 성능이 달라집니다. 때문에 피벗을 선택하는 방법에도 개선안이 존재합니다.
-
Median of Three
-
Dual Pivot
-
Random Pivot
Median of Three :
정렬 대상의 [처음, 중간, 마지막] 값 중 중간값을 피벗으로 선정합니다. 이러면 피벗이 자료를 균등하게 나눌 가능성이 높아지기 때문에 정렬 성능이 좋아질 확률도 높아집니다.
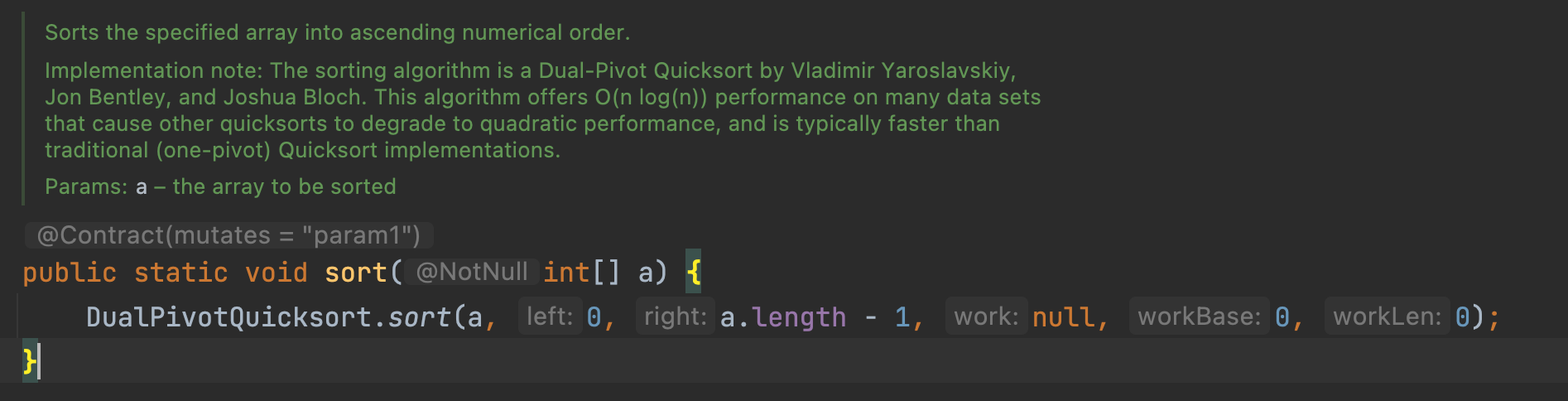
Dual Pivot:
피벗을 2개 두고, 구간을 3개로 나누어 quick sort를 진행하는 것
Java의 Arrays.sort()에서 이 방식을 사용합니다
-
-
Worst case의 시간복잡도는 O(n^2)입니다. 이 케이스는 피벗이 자료의 최소, 혹은 최대값으로 정해졌을 때 발생합니다
하지만 보편적으로 좋은 성능을 보이기 때문에, 자주 이용되는 정렬 알고리즘입니다
6. 병합 정렬 (Merge Sort)
- 분할 정복(divide and conquer) 알고리즘입니다
- Worst case에서도 O(nlogn) 시간 내에 동작하는 정렬 알고리즘입니다
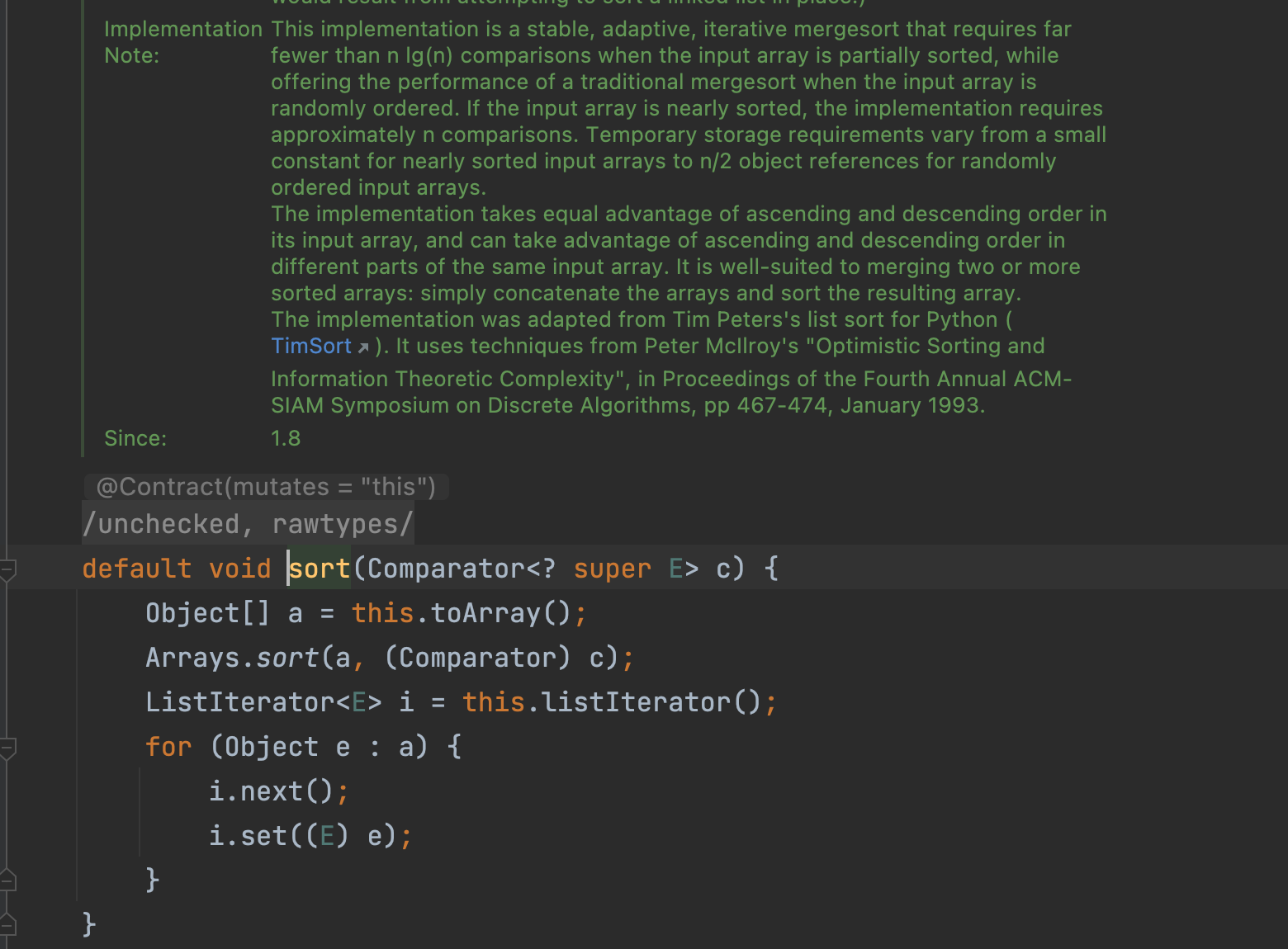
팀 정렬 (Tim Sort):
병합 정렬에 삽입 정렬을 적용해서 개선한 정렬 알고리즘입니다. Divide된 자료가 일정 크기보다 작을 때는 삽입 정렬을 사용해서 정렬 속도를 끌어 올립니다.
Java의 Collections.sort()에서 이 방식을 사용합니다.
7. 계수 정렬
-
비교를 통한 정렬이 아닙니다
그래서 비교 정렬 알고리즘의 시간복잡도 한계인 O(nlogn)보다 빠른 O(n) 시간 내 동작이 가능합니다
비교 정렬 알고리즘의 한계를 돌파해야 할 필요가 있을 때 계수 정렬을 고려해 볼 수 있습니다 -
시간복잡도 O(n+k)에서 k는 자료의 범위입니다. n과 k중 큰 값이 시간복잡도를 지배합니다
ex) 1 ~ 500 사이의 수를 정렬할 때, k는 500 / 1 ~ 2억 사이의 수를 정렬할 때, k는 2억 -
k가 클 경우, 메모리가 심각하게 낭비될 수 있습니다
-
보통 문자열 관련 정렬에서 높은 효율성을 보입니다 (알파벳의 경우 k가 26)
8. 기수 정렬
-
비교를 통한 정렬이 아닙니다
-
비교하지 않고 정렬하는 장점을 극대화하기 위해 보통 계수 정렬을 도입하여 사용합니다
-
이 경우 시간복잡도는 O(d(n+k))가 되고, 여기서 d는 차원의 수, k는 자료의 범위입니다.
ex) 1 ~ 500 사이의 수를 정렬할 때, d는 3(세자리 수), k는 500입니다. -
따라서 d와 k를 고려하여 사용 여부를 결정해야 합니다. 상황에 따라 비교를 통한 정렬이 나을 수도 있기 때문입니다
-
기수 정렬은 각 기수(숫자에서 각 자리와 같은 개념)를 정렬하기 위해 다른 정렬 알고리즘을 필요로 합니다
이 때 도입되는 알고리즘은 stable한 정렬 알고리즘이어야 합니다(보통은 위에서 언급한 것 처럼 계수 정렬을 사용합니다)