[추천 시스템] 추천 시스템이란?

Mineru·2022년 10월 3일

그럼 추천 시스템은 뭐니?

추천 시스템은 사람들의 과거 행동을 기준으로 무언가를 추천하는 시스템이다.

추천 시스템은 고객의 취향과 흥미를 알아낼 수 있는 데이터를 수집하는 것에서부터 시작한다. 그런 다음 다른 유저들의 집단행동에 병합하여 고객들이 좋아할 만한 것들을 추천하는 것이다.

추천 시스템의 종류에는 뭐가 있니?

Top-N Recommand
Content-based Filtering
Collaborative Filtering
Model-based Collaborative Filtering

Top-N Recommand

Top-N 추천 시스템은 멜론 차트 100을 생각할 수 있겠지만 멜론 차트 100은 추천 시스템이 아니다.
왜냐하면 사용자 A와 사용자 B가 멜론 차트 100를 봤을 때 결과가 항상 같기 때문이다.
각 사용자의 행동 데이터를 기반으로 추천을 하지 않았기 때문에 멜론 차트 100는 추천이라고 할 순 없다.

Top-N 추천 시스템은 각 사용자의 관심사를 나타내는 데이터를 저장하는 것으로부터 시작한다. 이러한 데이터를 우리는 유저 행동 데이터라고도 부른다.

어떠한 추천 시스템을 만들든 항상 다음과 같은 큰 맥락으로 추천 시스템은 동작한다.

추천을 위한 후보군 생성
추천하고자 하는 상황에 맞는 필터링
아이템 간 연관성 분석
순위 정렬

암묵적 / 명시적 피드백

추천 시스템에서 유저 행동 데이터를 볼 때, 두가지의 맥락으로 유저 행동 데이터를 바라봐야 한다.

Implicit feedback: 은연중인, 내재적인 피드백, 암묵적 피드백
Explicit feedback: 명백한, 외재적인 피드백, 명시적 피드백

암묵적 피드백의 예시

클릭
시청 시간, 체류 시간, 컨텐츠 소비 시간
구매

명시적 피드백의 예시

별점 평가
좋아요 / 싫어요

Content-based Filtering

컨텐츠 기반 필터링은 유저 행동 데이터의 합계는 사용하지 않고 추천 항목 자체의 Feature만 고려하여 새로운 아이템을 추천하는 방법을 말한다.

컨텐츠 기반 필터링은 TF-IDF, Word2Vec(NLP에서만 사용 되는 방법)와 같은 Feature Extraction 방법론이 사용된다.
추출 된 Feature를 통해 아이템 간의 유사도는 코사인 유사도, 유클리어드 유사도, 자카드 유사도, 피어슨 상관관계를 통해 측정된다.

유사도 함수들을 통해 각각 순위를 매긴 후 정렬을 한다.

계산 된 각 아이템 간의 유사도를 통해, 어떤 유저가 특정 아이템을 선호할 때 유사한 top 10 아이템을 추천한다.

Collaborative Filtering

협업 필터링 추천은 유저 & 아이템의 관계로부터 도출되는 추천 시스템이다.

협업 필터링의 장점으로는 아이템의 상세 정보 없이 추천이 가능하지만, 단점으로는 유저 행동 데이터가 부족한 시기인 초기 단계에서는 추천이 어렵다는 점과 유저와 아이템의 수가 많아질수록 연산해야할 행렬이 기하급수적으로 많아진다는 점이다.

협업 필터링 추천은 크게 두가지로 분류 된다.

Memory Based Approach
- User Based Collaborative Filtering
- Item Based Collaborative Filtering
Model based Approach

User-Based Collaborative Filtering

유저 기반 협업 필터링은 각 사용자들의 평가 이력을 기반으로 추천을 하는 방식을 말한다.

Item-Based Collaborative Filtering

아이템 기반 협업 필터링은 특정 아이템을 좋아했던 내역을 보고 이를 비슷하게 평가한 유저에게 추천을 하는 방식을 말한다.

일반적으로 유저 기반 협업 필터링 보다 아이템 기반 협업 필터링이 났다.

아이템이 유저보다 영구적인 속성을 더 가지는 경향이 있음.
아이템이 유저보다는 매우 적게 있다는 것.

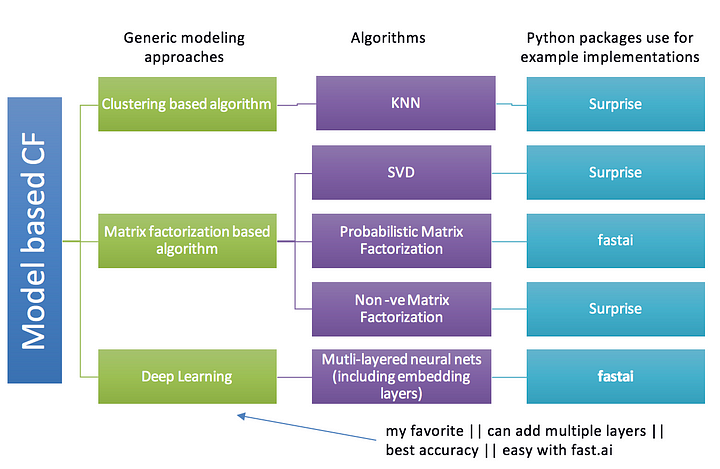
Model-based Collaborative Filtering

모델 기반 협업 필터링 추천과 유저/아이템 기반 협업 필터링의 큰 차이점은 어려운 용어인 Parametric Maching Learning 사용 여부의 그 차이점이 있다.

Parametric Maching Learning란?

Gradient Descent(경사 하강 알고리즘)와 같은 Optimization 방법으로 Parameter를 업데이트하는 방식을 말함.
Parametric 모델은 모델의 파라미터 수가 정해져 있는 모델을 의미함.

Matrix Factorization(MF, 행렬 인수 분해)

MF의 기본 아이디어는 "사용자의 선호도가 몇개의 Hidden Factors"로 결정 될 수 있다는 것이다. 이러한 Factors를 Embeddings라고 부른다.

Embeddings란?

임베딩이란 고차원 벡터를 저차원 벡터로 변환한 결과를 말한다.

위 그림의 첫번째 그림인 2차원 벡터 공간이 아닌 두번째, 세번째 1차원 벡터 공간의 곱으로 표현하여 행렬 분해를 하게 되면 데이터를 저장하는 데 필요한 공간. 즉, 메모리 크기를 줄일 수 있다는 장점을 가지게 된다.

행렬 분해(Matrix Decompoision)는 손실 함수(loss function)와 제약(constraints)에 대한 최적화(optimization)로 여겨질 수 있다.
제약은 모델의 특성에 따라 선택되는데 예를 들면, 음수 미포함 행렬 분해(Non-negative matrix decomposition)는 resultant matrices가 non-negative 원소들을 갖기를 원하는 경우인데, 여기서는 non-negative 조건이 constraints가 된다.

Embeddings는 아이템과 사용자의 Low Dimensional Hidden Factors라고 이해하면 된다.

위 그림의 첫번째 사진은 User들이 평가한 Movie들의 각 평점이다. 실제 모델링을 할 때는 평점 외에도 다른 Feature들이 상황에 따라 달라질수도 있다.
최종적으로 추천을 할 때는 1차원 벡터 공간 두개의 스칼라곱(Dot Product)을 통해 추천 된 내용에 대해 평가할 수 있다.

SVD(Singular Value Decomposition, 특이값 분해)

(작성중...)

Probabilistic Matrix Factorization(PMF, 확률 기반 행렬 분해)

PMF 구현 코드

PMF는 user가 item에 주는 점수값이 정규 분포(Gaussian 분포)를 가진다고 가정한 모델이다.

\begin{array}{lcl} p(R|U, V, \sigma^2) = \textstyle \prod_{i=1}^N \textstyle \prod_{j=1}^M \bigl[ \mathcal{N} (\mathcal{R}_{ij} | U_i^T V_j, \sigma^2) \bigr] \\ \\ U : \text{User Iatent Matrix} (U \in R^{DxN}) \\ V : \text{Item Iatent Matrix} (V \in R^{DxM}) \\ \sigma^2 : \text{분산값 (Hyperparameter)} \\ R_{ij} : \text{user i의 item j에 대한 점수} \\ U_i^T : \text{User i의 latent vector} \\ V_j : \text{item j의 latent vector} \\ I_{ij} : \text{user i가 item j에 점수가 있으면 1, 없으면 0} \\ N : \text{user 개수} \\ M : \text{item 개수} \\ D : \text{latent 변수 개수} \\ \end{array}

위 수식이 의미하는 바는 다음과 같다.
우리가 가진 데이터에서 점수 집합 R이 나올 확률은 각 User와 Item의 Latent Vector를 곱한 값을 평균으로, σ^2를 분산값으로 가진 정규분포들의 곱으로 구성된다는 것이다.
여기서 U와 V 또한 정규 분포를 따르는 행렬로 가정하고 있다.

\begin{array}{lcl} p(U | \sigma_U^2) = \textstyle \prod_{i=1}^N \mathcal{N} (U_i | 0, \sigma_U^2 \mathbf{I}) \\ p(V | \sigma_V^2) = \textstyle \prod_{j=1}^M \mathcal{N} (V_j | 0, \sigma_V^2 \mathbf{I}) \end{array}

위 수식을 정리하자면 다음과 같다.

점수값들은 User와 Item Latent Vector의 내적을 평균값으로, 분산값을 σ^2를 가진 정규분포로 구성
각 User와 Item Latent Matrix는 평균이 0, 분산이 σ_U^2, σ_V^2인 정규분포로 구성

이러한 분포들과 베이즈 룰을 활용하면 다음과 같은 식이 된다.

p(U, V | R, \sigma^2, \sigma_V^2, \sigma_U^2) \propto p(R|U, V, \sigma^2) p(U | \sigma_U^2) p(V | \sigma_V^2)

좌변식은 우리가 모델 파라미터를 구할 때 활용했던 MAP(Maximum a Posterior) Estimation에서 볼 수 있는 식이다. U, V를 구하고자 하는 파라미터로 보고 R, σ^2, σ_V^2, σ_U^2를 주어진 값으로 보면

p(\theta | X, Y)

와 유사한 구조가 된다.

우변식은 우리가 위에서 본 식들로 구성되어 있다.
즉, 우리가 가진 식들을 활용한다면 좌변 부분을 만들 수 있다.
이를 활용해 log 목적 함수(손실 함수)를 만들면 다음과 같은 구조로 된다.

\begin{array}{lcl} p(U, V | R, \sigma^2, \sigma_V^2, \sigma_U^2) \\ \propto p(R|U, V, \sigma^2) p(U | \sigma_U^2) p(V | \sigma_V^2) \\ \propto p(R|U, V, \sigma^2) + p(U | \sigma_U^2) + p(V | \sigma_V^2) \\ \propto \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^M I_{ij} (R_{ij} - U_i^T V_j)^2 + \frac{\lambda_U}{2} \sum_{i=1}^N {\lVert U_i \rVert}_{Fro}^2 + \frac{\lambda_V}{2} {\lVert V_j \rVert}_{Fro}^2 \\ = E \end{array}

목적함수 E에 대한 수식이 완성되었다.
R, σ^2, σ_V^2, σ_U^2 등은 이미 주어진 값이며 학습이 가능한 값은 U, V 이다. 그렇기 때문에 두 값을 활용해 이 목적함수 값을 최소화 시키는 값을 찾아야한다.
식이 2차식이라 U, V를 미분했을 때 최적값이 나오므로 이를 활용해 Gradient를 구한다.

\begin{array}{lcl} \frac{\delta E}{U_i} = \sum_{j=1}^M (I_{ij}(R_{ij} - U_i^T V_j)) V_j + \lambda_U U_i \\ \text - \lambda_U = \frac{\sigma^2}{\sigma_U^2} \\ \frac{\delta E}{V_i} = \sum_{i=1}^N (I_{ij}(R_{ij} - U_i^T V_j)) U_j + \lambda_V V_j \\ \text - \lambda_V = \frac{\sigma^2}{\sigma_V^2} \\ \end{array}

이를 활용해 모델을 학습시키게 된다.

Non-negative Matrix Factorization(NMF, 음수 미포함 행렬 분해)

NMF는 음수를 포함하지 않는 행렬 X를 음수를 포함하지 않는 행렬 W와 H의 곱으로 분해하는 알고리즘이다.

또한, NMF는 데이터 셋에서 특징을 추출하는 방법으로 차원축소(Dimension reduction) 등을 위해 활용될 수 있는 방법이다. PCA(주성분분석), SVD(특이값분해), ICA(독립성분분석)와 같은 계열의 데이터 분석 방법이다.

앞에서 봤던 그림에서 두번재 그림에 해당 되는 영역이 가중치 행렬이 되고, 세번째 그림에 해당 되는 영역이 특징(Feature) 행렬이 된다.

아이템의 각 특성들을 나열한 행렬과 사용자의 해당 특성들 간의 가중치를 나열한 행렬로 구성하고 이를 곱하게 되면 원본 데이터로 돌아오게 된다.

이러한 NMF는 여러 개의 값으로 구성된 데이터를 가중치행렬과 특성행렬로 분리하는 것을 방법이다.
이때, 데이터의 가중치 행렬과 특성 행렬은 어떻게 찾을 수 있을까?
무작위로 구성 된 매트릭스를 시작으로 최종적으로 만들어지는 값이 데이터 값으로 구성 되는 방향으로 여러 번 학습이 진행되게 된다.

Non-parametric approach

Non-parametric approach의 아이디어는 Memory-based 추천 시스템의 아이디어와 동일하다.
Memory-based 알고리즘에서 우리는 예측을 하기 위해, 사용자 간의 또는 아이템 간의 유사도를 가중치로 사용한다.

Non-parametric approach와 Memory-based 추천 시스템의 차이는 유사도를 측정할 때 Memory-based는 코사인, 피어슨 등과 같은 방법으로 유사도를 측정하는 반면 Non-parametric approach는 비지도 학습 모델을 사용한다는 것이다.
Non-parametric approach는 유사한 사용자들의 수를 k와 같은 수로 한정지어 시스템을 더 확장가능하게 만든다.

KNN(K-Nearest Neighbor, k-최근접 이웃)

KNN 알고리즘은 데이터로부터 거리가 가까운 k개의 다른 데이터의 라벨을 참조하여 분류하는 알고리즘으로 거리를 측정할 때 유클리디안 거리 계산법을 사용한다.

Real-Data를 가지고 테스트를 해보지 않고서는 협업 필터링 추천 시스템을 평가하기는 어렵다.
협업 필터링 추천은 순위 예측을 기초로 하지 않기 때문에 오프라인에서의 정확도를 측정할 수는 없다. 따라서 협업 필터링이라는 개념은 순위 예측을 하는 추천 시스템에 적용되기 때문에 일반적으로 KNN 추천이라고 불린다.

순위 예측을 기반으로 하는 추천 시스템의 구조에서는 사용자가 아직 평가하지 않은 것들의 순위를 예측해서 추천 후보군을 만들어 낸다.
그리고 가장 높은 예측 순위 중에서 상위 k개의 아이템을 선택한다.
이러한 방법은 효율적이지 않지만 순위를 예측하는 시스템의 오프라인 정확도를 훈련/테스트나 교차 검증을 통해서 측정할 수 있게 된다.

여기서 문제가 되는 점은 순위를 예측할 때 아이템이나 사용자 유사도를 사용하기 때문에 이것은 여전히 협업 필터링으로 불린다는 것이다.

사용자 기반 KNN

사용자 기반 KNN에서는 다음과 같이 작동한다.

사용자나 아이템에 대한 순위를 예측하기 때문에 우리가 관심이 있는 사용자와 비슷한 사용자를 찾은 것으로부터 시작한다.
하지만 이 사용자는 관심이 있는 아이템을 평가한 사람이어야 한다. 우리는 이를 비슷한 k명의 사용자로 제한한다.
결국 k명의 비슷한 사용자들로부터 아이템에 대한 순위 세트라는 결과를 얻게 되고,
이것들이 KNN이고 이 사용자가 우리가 예측해야 하는 사용자와 얼마나 비슷한지를 측정한다.

그 다음으로 순위 그 자체를 가중해서 관련 순위에 대한 사용자 유사도 스코어를 가중치의 평균을 구할 것이다.
이 방법을 이용하면 아이템을 평가했던 비슷한 사용자를 기반으로 사용자가 어떤 평가를 할지 그럴듯한 예측을 할 수 있다.

우리는 이 방법이 사용자 기반 협업 필터링과 유사하다는 것을 알 수 있다. 하지만 두 동작 방식은 완전히 다르다.
이는 사용자 대 사용자 유사도 행렬을 핵심으로 하므로 나와 비슷한 것을 좋아했던 사람에게는 추천하지 않는다.
대신에, 데이터에 깊이 파고 들어서 가능한 모든 경우의 아이템과 사용자에 대한 순위를 예측한다.
이는 더 복잡한 접근이고 보통은 안 좋은 방법이다.

\hat{r}_{ui} = \frac{\sum{}_{v \in N_i^k(u)}sim(u, v) \cdot r_{vi}}{\sum_{v \in N_i^k(u)} sim(u,v)}

서프라이즈 라이브러리에 따르면 사용자의 u와 아이템 i의 예측 순위는 k명의 비슷한 사용자를 합한 값과 같다.
여기서 k명의 비슷한 사용자들을 v라고 한다.
사용자 u와 v의 유사도 스코어를 모두 더한 다음에 사용자 v가 평가한 순위를 곱한다.
그 다음에 사용자 유사도 스코어의 합으로 나누어 준다. 가중 평균을 낸 것이고 이는 순위 예측에 사용 될 수 있다.

아이템 기반 KNN

아이템 기반 KNN도 사용자 기반 KNN과 같은 방법으로 작동한다.

사용자와 아이템이라는 단어를 서로 바꿔봤다. 그러고나니 아이템 i에 대한 사용자 u의 순위를 예측하려면 k개의 아이템 세트로 시작해야 한다.
이는 아이템 i와 가장 비슷한 사용자에 의해 평가된다. 거기서부터는 같은 과정이다. 순위의 가중 평균을 계산한다면 꽤 신뢰할 만한 순위 예측을 할 수 있을 거다.

\hat{r}_{ui} = \frac{\sum{}_{j \in N_u^k(i)}sim(i, j) \cdot r_{uj}}{\sum_{j \in N_u^k(j)} sim(i,j)}

사용자 기반 KNN 수식과 다른 점은 사용자 u와 v 대신에 아이템 i와 j를 사용했다는 점이다. 다시 한번 예측 순위는 k개의 가장 비슷한 아이템 세트를 기초로 한다.
이 아이템 세트는 문제가 되는 아이템을 사용자가 평가한 것이다. 순위에 따라 가중된 아이템 유사도 스코어를 모두 더한 뒤에 유사도 스코어의 합계로 나눠준다.
이는 협업 필터링이라는 개념을 순위 예측이라는 틀 안에 넣었다는 점에서 안 좋아 보일 수도 있지만 앞으로 살펴보겠지만 꽤 괜찮은 순위 예측법이다.
만약 당신의 목표가 상위 N개의 추천 목록을 만드는 것이라면 더 단순하고 직관적인 이전에 살펴봤던 접근을 사용하는 것이 나을 것이다.

다양한 KNN 매개변수로 실험

알고리즘의 파라미터를 변경하는 방법으로 어느 정도 결과를 향상 할 수도 있다.

코사인 유사도
MSD(Mean Squared Difference) 유사도
피어슨 유사도

RMSE의 점수는 크게 중요하지 않다. 실제 추천 항목을 보면서 이것이 진정으로 제대로 된 추천인지 아닌지를 비교하면서 더 현실적으로 맞게 추천한 항목으로 추천한 유사도를 선정하는 것이 좋을 것이다.

KNN을 제대로 사용하고자 한다면 순위 예측용보다는 순위 분류용으로 생각하는 것이 더 적절하다.
KNN은 아주 예민하고 드문 데이터이지만 10만 개의 순위를 만들어내는 것이 아니라면 더 나은 결과를 얻을 수도 있다.

하지만 가장 중요한 점은 정확도가 전부가 아니라는 것이다. KNN이 압도적인 결과를 내는 주된 원인은 잘못 된 문제를 해결하려 하기 때문이다.

Neural Nets / Deep Learning

인공신명망을 이용하여 user latent features와 item latent features를 업데이트해 최종 순위를 구하는 것이 인공신명망을 사용한 추천의 목적이다.

인공신경망을 이용한 추천을 행렬 분해의 확장판이라고 생각할 수 있다.

SVD나 PCA에서 기존 희소 행렬(original sparse matrix)을 두 개의 low rank 직교행렬(orthogonal matrix)로 분리하는데, 인공신경망에서는 꼭 나눠진 matrix가 직교행렬일 필요가 없다. 그저 embedding matrices의 값들을 업데이트하는 것에 초점을 맞춘다.

user latent features와 item latent features는 나중에 linear, non-linear layers의 input이 된다.
이러한 input은 relu, sigmoid layers에 넣어져 optimization 방법에 따른 가중치를 배우게 된다.

Hybrid Filtering

콘텐츠 기반 필터링과 협업 필터링은 장단점이 있기 때문에 두 방법을 같이 활용하는 방법을 Hybrid Filtering이라고 한다.

정리

다양한 파생 방법론이 있지만, 대표적으로 데이터가 적은 스타트업들이나 초기 단계 서비스를 운영하는 팀에서는 콘텐츠 기반 필터링으로 하다가 어느 정도 데이터가 누적이 되면 협업 필터링으로 변경하는 전략을 가진다고 한다.

출처

Mineru

Daily Coding

이전 포스트

[추천 시스템] 추천 시스템 사례

다음 포스트