[CS224W GraphML] 2-3. Graph 클러스터링: Laplacian, Node Clustering

Minjoo Lee·2021년 8월 16일

Graph-ML

목록 보기

4/4

Graph Representation Learning Book의 Chapter2을 번역, 요약, 정리했습니다.

[2.1 Graph 통계량]과 [2-2. Graph 이웃관계]에 이어서 이후 장들의 기초가 되는 배경지식과 고전적인 Graph ML 방법을 소개합니다. (추가로 수식 전개보다는 결과 성질에 초점을 맞춰 다룰 예정입니다.)

2.3 Graph Laplacians and Spectral Methods

이번 장에서는 Graph에 속한 Node들의 클러스터를 학습하는 방법을 다룹니다. Node들을 저차원 공간으로 임베딩할 수 있는 학습 방법의 기초가 됩니다. 우선 Graph를 푱현하는 여러 중요한 행렬의 정의와 Spectral Graph Theory 스펙트럼 Graph 이론을 간략하게 소개합니다.

2.3.1 Graph Laplacians

Adjacency 인접행렬은 Graph의 정보를 그대로 표현할 수 있습니다. 하지만 Laplacians 이라 불리는 인접행렬을 변형한 다른 행렬 표현방식이 존재합니다.

Unnormalized Laplacian

가장 기초적인 Laplacian 행렬은 Unnormalized Laplacian입니다.
$D$ 는 대각선이 각 행 Node의 자유도를 나타내는 자유도 행렬입니다.
$A$ 는 인접해렬을 나타냅니다.

L = D - A L_{i, j} = \begin{cases} d_{v_i}, & \text{if } i = j \\ -1 & \text{if } i \neq j \text{ and } (v_i, v_j) \in E \\ 0 & \text{otherwise} \end{cases}

이 Laplacian 행렬을 중요한 속성을 갖고 있습니다. Positive semi-definite 행렬이고, N개의 음이 아닌 고유값을 가집니다. 중요 속성을 이용하면 다음 정리를 얻을 수 있습니다.

Theoram 2. Laplacian의 고유값 0의 개수는 Graph 안에 연결된 컴포넌트 수와 같습니다.

연결된 컴포넌트에 속한 Node들은 고유벡터의 값이 모두 동일합니다. Fully Connected Graph (완전 Graph)라면 고유값이 0인 경우는 한 가지이며, 이때의 고유벡터는 모든 값이 1인 벡터입니다.

여러 분리된 컴포넌트를 가지는 Graph의 Laplacian 행렬은 원래 Graph 내에서 K개의 Fully Connected Subgraph들의 Laplacian 행렬로 나눌 수 있습니다. 이 경우 고유값 0에 해당하는 고유벡터를 Subgraph의 수 K개 만큼 갖게 되고, 각 고유벡터는 각 컴포넌트의 Indicator가 됩니다.

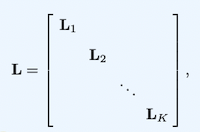
아래 Graph1에 대해 고유값과 고유벡터를 이용해 컨포넌트 개수를 확인하는 과정의 코드르 추가합니다.

[Graph1]

import numpy as np
import networkx as nx

# Graph를 할당합니다.
A = np.array([
    [0, 1, 1, 1, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [1, 1, 0, 0, 0, 0],
    [1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1],
    [0, 0, 0, 0, 1, 0],
])

labels={0: "A", 1: "B", 2: "C", 3: "D", 4:"AA", 5: "BB"}

G = nx.Graph(A)

# Degree Matrix를 할당합니다.
n = A.shape[0]

D = np.zeros((n, n))
for label, degree in G.degree:
    D[label, label] = degree

print(D)
# array([[ 3., -1., -1., -1.,  0.,  0.],
#        [-1.,  2., -1.,  0.,  0.,  0.],
#        [-1., -1.,  2.,  0.,  0.,  0.],
#        [-1.,  0.,  0.,  1.,  0.,  0.],
#        [ 0.,  0.,  0.,  0.,  1., -1.],
#        [ 0.,  0.,  0.,  0., -1.,  1.]])

우선 Graph1을 networkx를 이용해 만들고, Laplacian 행렬을 정의 합니다.

# numpy를 이용해 고유값과 고유벡터를 계산합니다.
eig_value, eig_vector = np.linalg.eig(L)

# float64를 보기 편하게 3자리 소수점으로 반올림합니다.
eig_value = eig_value.round(3)
eig_vector = eig_vector.round(3)

# 고유값을 기준으로 오름차순으로 정렬합니다.
sortidx = np.argsort(eig_value)

eig_value = eig_value[sortidx]
eig_vector = eig_vector[:, sortidx]

numpy를 이용해 Laplacian 행렬의 고유갑과 고유벡터를 계산하고, 고유값이 작은 순서로 정렬합니다. 이때 eig_value[i]에 해당하는 고유벡터는 eig_vector[:. i]로 찾을 수 있습니다.

print(eig_value)
# array([0., 0., 1., 2., 3., 4.])

[Graph1]의 이미지에서 컴포넌트가 2개임을 알 수 있고, 고유값이 0인 경우가 2번인 것도 확인 가능합니다.

print(eig_vector)
# array([[-0.5  ,  0.   , -0.   ,  0.   ,  0.   ,  0.866],
#        [-0.5  ,  0.   , -0.408,  0.   , -0.707, -0.289],
#        [-0.5  ,  0.   , -0.408,  0.   ,  0.707, -0.289],
#        [-0.5  ,  0.   ,  0.816,  0.   , -0.   , -0.289],
#        [ 0.   ,  0.707,  0.   ,  0.707,  0.   ,  0.   ],
#        [ 0.   ,  0.707,  0.   , -0.707,  0.   ,  0.   ]])

각 고유값에 해당하는 고유벡터입니다. 첫번째 열은 0 ~ 3번 행인 Node (A, B, C, D)에 대해 값을 가져 4개의 Node가 하나의 컴포넌트임을 알 수 있습니다. 두번째 열은 4 ~ 5번 행인 Node (AA, BB)에 대해 값을 가져 2개의 Node가 하나의 컴포넌트임을 알 수 있습니다. 위에서 고유값이 0인 경우 원소가 1인 고유벡터를 갖는 다고 했지만, numpy 내에서 벡터의 길이가 1이 되도록 정규화를 하기 때문에 다른 값을 가지게 됩니다.

Normalized Laplacian

정규화를 적용한 Laplacian 행렬도 있습니다.

먼저 Symmetric Normalized Laplacian 입니다.

L_{sym} = D^{-\frac{1}{2}} L D^{-\frac{1}{2}}

또 다른 Random Walk Laplacian입니다.

L_{RW} = D^{-1} L

2.3.2 Graph Cuts and Clustering

2.3.2에서 고유값 0에 해당하는 고유벡터가 연결된 컴포넌트의 Indicator임을 다뤘습니다. 하지만, 이렇게 연결된 컴포넌트끼리 하나의 클러스터라고 하는 것은 의미가 없습니다. 이번 장에서는 Fully Connected된 하나의 Graph내에서 Node들을 최적으로 클러스터링하는 방법을 소개합니다.

Graph Cuts

가장 먼저 최적 클러스터가 무엇인지 정의해야 합니다. 이를 정의하기 위해 먼저 Graph의 cut을 먼저 정의합니다.

$A$ 는 전체 Node의 부분집합입니다. 이때 $\bar{A}$ 는 $A$ 의 여집합에 해당합니다. Graph의 Node들을 겹치지 않는 K개의 부분 집합인 $A_1, ... A_K$ 로 먼저 정의하겠습니다.

cut(A_1, ... A_K) = \frac{1}{2} \sum^{K}_{k=1} | (u,v) \in E : u \in A_k, v \in \bar{A_k}|

cut 이란 단순히 Node 집합들 사이 경계에 걸려 있는 Edge의 수 입니다. 최적 클러스터는 이 cut 의 값을 최소화 하는 것입니다.

하지만 이렇게 할 경우, 하나의 클러스터에 대해 하나의 Node만 남도록 최적화될 수 있습니다. cut 을 최소화 하면서 클러스터의 크기가 적당히 크도록 적용한 것이 RatioCut입니다. 다시말해 클러스터의 크기가 작은 경우 패널티를 부여합니다.

RatioCut(A_1, ... A_K) = \frac{1}{2} \sum^{K}_{k=1} \frac{| (u,v) \in E : u \in A_k, v \in \bar{A_k}|}{|A_k|}

다른 방식으로 Nomalized Cut(NCut)이 있습니다. 부분집합에 속한 Node들의 자유도 합이 비슷해지도록 패널티를 부여합니다.

NCut(A_1, ... A_K) = \frac{1}{2} \sum^{K}_{k=1} \frac{| (u,v) \in E : u \in A_k, v \in \bar{A_k}|}{vol(A_k)}, vol(A) = \sum_{u \in A}d_u

위에서 정의한 3가지의 cut 를 최소화하는 것이 최적 클러스터라 할 수 있습니다.

Approximating the RatioCut with the Laplacian Spectrum

Laplacian Spectrum을 이용해 RatioCut 최소화하는 클러스터를 찾는 과정을 근사시킬 수 있습니다.

가장 먼저 Fully Connected Graph를 단순히 두 개의 클러스터 $A$ , $\bar{A}$ 로 나누는 경우 입니다.

이때는 Laplacian 행렬의 두번째로 작은 고유벡터를 이용합니다. (n번째로 작은 고유벡터란, n번째로 작은 고유값에 해당하는 고유벡터를 의미합니다.) 두번째로 작은 고유벡터를 이용하는 이유는 가장 작은 고유값은 언제나 1이고 고유벡터의 원소들은 모두 동일하기 때문입니다.

두번째로 작은 고유벡터 $a$ 에서 원소가 0이상인 Node를 하나의 클러스터, 0보다 작은 Node를 하나의 클러스터로 볼 수 있습니다.

\begin{cases} u \in A, & \text{if } a[u] \ge 0 \\ u \in \bar{A} & \text{if } a[u] < 0 \\ \end{cases}

위 과정을 아래 Graph2에 적용해 보겠습니다.

[Graph2]

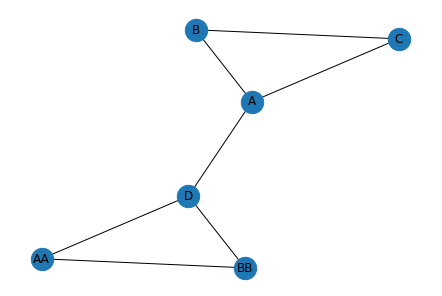
A = np.array([
    [0, 1, 1, 1, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [1, 1, 0, 0, 0, 0],
    [1, 0, 0, 0, 1, 1],
    [0, 0, 0, 1, 0, 1],
    [0, 0, 0, 1, 1, 0],
])

G = nx.Graph(A)

새로운 Graph2를 할당합니다. Laplacian 행렬 생성 과정을 생략하겠습니다.

print(L)
# array([[ 3., -1., -1., -1.,  0.,  0.],
#        [-1.,  2., -1.,  0.,  0.,  0.],
#        [-1., -1.,  2.,  0.,  0.,  0.],
#        [-1.,  0.,  0.,  3., -1., -1.],
#        [ 0.,  0.,  0., -1.,  2., -1.],
#        [ 0.,  0.,  0., -1., -1.,  2.]])

정렬된 고유값과 고유벡터 계산 과정도 생략하겠습니다. Graph2는 완전Graph로 고유값 0을 같는 경우는 한가지 입니다.

print(eig_value)
# array([0.   , 0.438, 3.   , 3.   , 3.   , 4.562])

두번째로 작은 고유벡터 second_smallest_eig_vector 는 아래와 같이 찾을 수 있습니다.

second_smallest_eig_vector = eig_vector[:, 1]
print(second_smallest_eig_vector)
# array([ 0.261,  0.465,  0.465, -0.261, -0.465, -0.465])

클러스터1은 second_smallest_eig_vector가 0 이상인 Node (0, 1, 2)번째에 해당하는 Node (A, B, C)입니다. 클러스터2는 second_smallest_eig_vector가 0 보다 작은 Node (3, 4, 5)번째에 해당하는 Node (D, AA, BB)입니다.

cluster_1 = np.where(second_smallest_eig_vector >= 0)[0]
cluster_2 = np.where(second_smallest_eig_vector < 0)[0]

print(cluster_1)
# array([0, 1, 2]

print(cluster_2)
# array([3, 4, 5])

2.3.3 Generalized spectral clustering

이번에는 위 과정을 확정해 임이의 숫자 K개로 클러스터링 하는 과정을 소개합니다.
이때는 K번째 까지 작은 고유 벡터를 이용합니다.

먼저 가장 작은 벡터를 제외하고 K번째 작은 벡터를 찾습니다.
```
K = 3
k_smallest_eig_vector = eig_vector[:, 1: K]
```

1번에서 찾은 K-1개의 고유벡터를 이용해 $U \in R^{|V|\times (K-1)}$ 행렬을 구성합니다.

print(k_smallest_eig_vector.shape)
# (6, 2)

print(k_smallest_eig_vector)
# [[ 0.261  0.577]
#  [ 0.465 -0.289]
#  [ 0.465 -0.289]
#  [-0.261  0.577]
#  [-0.465 -0.289]
#  [-0.465 -0.289]]

각 Node를 행렬 $U$ 의 행들로 표현합니다. $z_u = U[u], \forall u \in V$
```
node_0 = k_smallest_eig_vector[0]

print(node_0)
# array([0.261, 0.577])
```
할당된 $z_u$ 를 이용해 K-means 클러스터링에 적용합니다.

이렇게 Graph 내에 있는 Node들을 클러스터링 하는 과정을 다뤘습니다. 마지막 과정은 Node 차원 축소의 모티브로 이후 강의에서 더 다룰 예정입니다.

Minjoo Lee

이전 포스트