Floyd Warshall 알고리즘

Floyd Warshall 알고리즘이란?

Dynamic Programming을 기반으로 한
그래프의 모든 정점에서 모든 정점으로의 최단거리를 구하는 알고리즘이다.
시간 복잡도는 O(n^3)이다.

개념에 대한 자세한 내용은 ▶ 플로리다 와샬 - 유튜브 강의를 보면 더 이해하기가 쉽다.

내 것으로 만들기 위해 직접 그려서 플로리다 와샬 알고리즘을 구현해보았다.
아래처럼 4개의 노드로 이루어진 그래프로 모든 최단 경로를 구해보자.

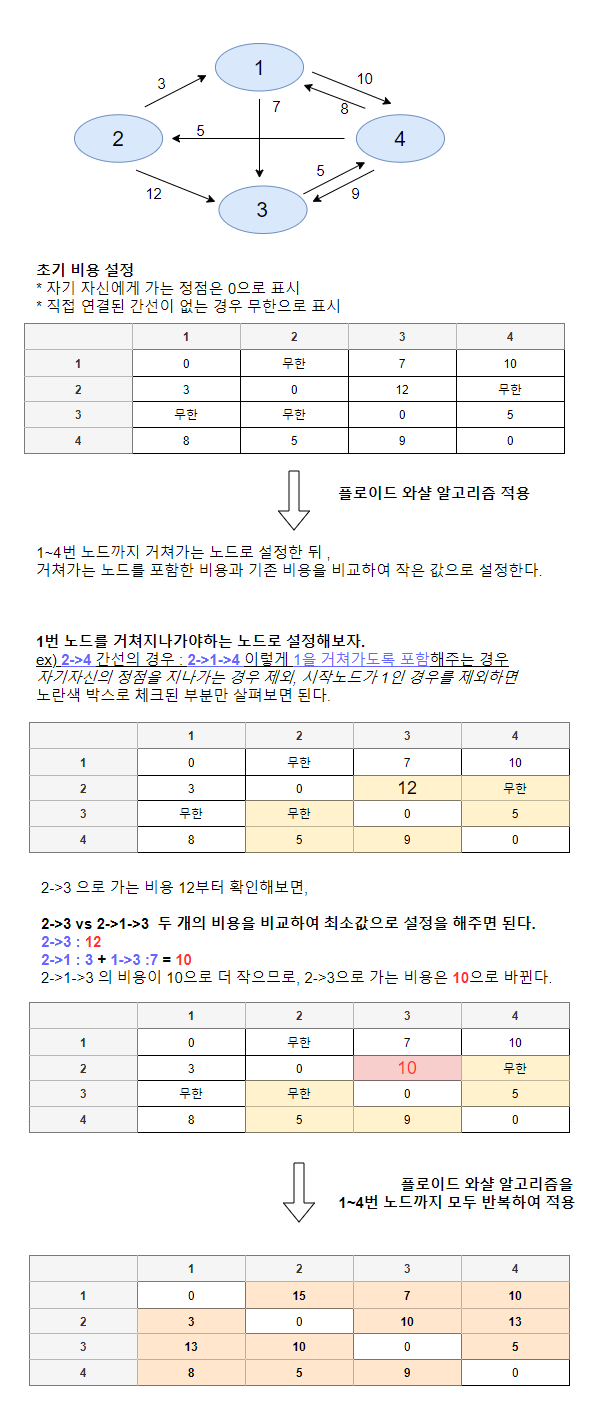
Floyd Warshall 코드로 이해하기

public void floyd_warshall() {
    
    int inf = 1000000;
    int[][] matrix = { {0, inf, 7 ,10},
                       {3, 0, 12 , inf},
                       {inf, inf, 0, 5},
                       {8, 5, 9, 0}};
    int n = matrix.length;

    // 플로리드 와샬 알고리즘
    // k : 거쳐가는 노드
    for(int k=0;k<n;k++){
        // i : 시작하는 노드
        for(int i=0;i<n;i++){
            // j : 도착하는 노드
            for(int j=0;j<n;j++){
                if(matrix[i][j] > matrix[i][k]+matrix[k][j]){
                    matrix[i][j] = matrix[i][k]+matrix[k][j];
                }
            }
        }
    }
}

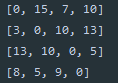
이와 같은 결과가 나온다.
전체 소스보기(git)

[참조블로그]

플로리다 와샬 알고리즘