[프로그래머스] 멀쩡한 사각형(Level 2)

📝문제 링크

프로그래머스 > Summer/Winter Coding(2019) > 멀쩡한 사각형 문제보기

🔑문제 KeyPoint

1. 최대공약수(gcd)를 이용하여 부분직사각형을 추출한다.
사실 첫접근은 비율로 계산을 했다.
8 * 12라면, 가장 작게 축소해서 회색 사각형의 개수를 구해보았다.
운이 좋게도 어제 유클리드 호제법을 이용한 최대공약수 문제를 풀었기에 최대공약수가 떠올랐다.
👉 유클리제 호제법을 이용한 문제 참고

2. 부분 직사각형 안에서 회색영역의 사각형의 개수 구하기

아무리 생각해도 규칙성을 찾을수가 없었다,,, 30분을 고민하다 구팀장님께 SOS!!

이 부분은 다른 블로그 풀이를 참고하였다. -> 참조블로그

부분 직사각형에서 제거되야 하는 개수 = w/gcd + h/gcd -1

직사각형의 대각선은 무조건 가로길이와 세로길이만큼은 지나간다. (이건 누구나 이해가능)
그렇다면, 왜 -1을 해주느냐???

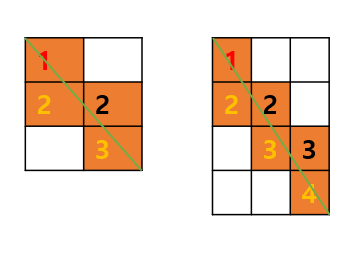
시작점은 빨간색1을 기준,
세로로 지나가는 칸은 노란색 / 가로로 지나가는 칸은 검정색
결국 빨간색1은 중복해서 지나가므로 -1을 해주어야 한다는 결론이다.

3. long 타입 계산주의

제한사항이 1억 이하의 자연수라는점!
모든 계산식에는 long타입으로 형변환을 해주지 않으면 오류가 난다

💻문제 풀이

우선 예외 케이스부터 제거,
넓이 또는 높이가 1인 직사각형 , 그리고 정사각형인 경우 우선적으로 처리해주었다.

    public static long solution(int w, int h) {

	long answer = 1;
		
        if(w == 1 || h == 1){			// 가로 또는 세로의 길이가 1인경우 사각형의 개수 0
            return 0;
        }
        long wl = (long) w;			// 모든 계산을 long타입으로 하기 위해 미리 형변환
        long hl = (long) h;
        
        if(wl == hl){				// 가로= 세로 길이가 같은 정사각형 인 경우 가로갯수만큼만 제외하면 됨
            return (wl*hl) - wl ;
        }
        
        long r = gcd(wl,hl);		// 최대공약수
        
        // 직사각형(w*h)의 넓이 - (제거할 사각형의 개수 * 최대공약수 개수)
        answer = wl*hl  - ((wl/r) + (hl/r) -1 ) * r;
        
		return answer;
    }
	
    /** 유클리드 호제법 - 최대공약수 구하기 */
    public static long gcd(long w, long h){
        while(h!=0){
            long r= w%h;
            w=h;
            h=r;
        }
        return w;
    }

전체 소스 보기