[프로그래머스] 입국심사(Level 3)

📝문제 링크

프로그래머스 > 이분탐색 > 입국심사 문제보기

🔑문제 KeyPoint

왜?🤷‍♀️🤷‍♂️ 이 문제가 이분탐색 분류에 있는지 이해하는게 가장 어려웠다.

처음 나의 접근은 times[]의 배수만큼 배열에 넣어준 뒤, 오름차순으로 정렬하여 답을 구하려 했다.

도대체 어떻게 이분탐색으로 접근을 해야하는가.....🤦‍♀️🤦‍♀️🤦‍♀️??
결국 구팀장에게 도움을 청하였다.

추정 시간값 / 각 심사관별 심사시간 = 심사관당 맡을 수 있는 입국자 수

그렇단다..이렇게 접근을 해야 이분탐색을 이용하여 풀 수 있다고 한다.
여기서 추정시간이라는게 이해가 안갔는데, 결국 추정시간이 답이다.
일단 추정시간값은 초기값으로 times[](가장 큰값) * n으로 설정해보자.

추정시간을 계산하여 n명이 될 때까지 이분탐색을 반복하여 답을 찾는다.

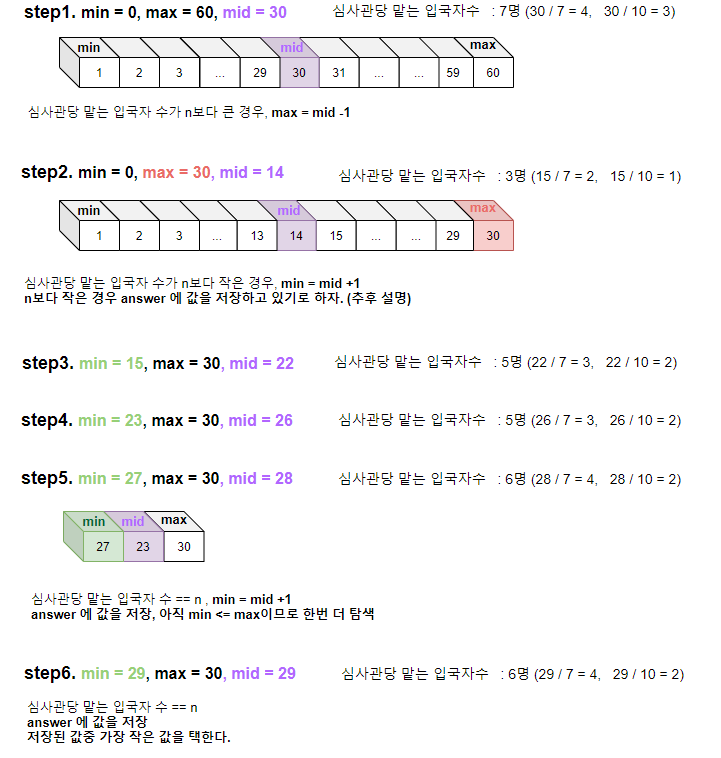
💻문제 풀이

처음에 찾는 sum=n값이 되면 , 그 닶을 찾고 break문으로 중단했다.
지금 현재 문제 28,29 둘 다 답이 될수 있으므로, n을 찾았다고 break문을 걸면 안 된다..!!

while(min <= max){ 
... 
... 생략
    if(n > sum){        // 최대값 범위를 줄여야 함
    	min = mid +1;
    }else{  
   	 max = mid -1;
    	if(sum == n){
		answer = mid;
    		break;
   	}
    }
}

그래서 수정한 코드는 다음과 같다.

public static long solution(int n, int[] times) {
    int len = times.length;
    long min = 0;                           // 최소값
    long max = new Long(times[len-1])*n;    // max : times의 최대값 * n명
    long answer = max;

    while(min <= max){                      // 최소값이 최대값보다 작을때까지만 반복
        long mid = (min+max) /2 ;
        long sum = 0;
        for(int i=0;i<len;i++){
            sum += mid / times[i];
            // sum > n보다 커지면, 더 이상 sum+= 계산 할 필요가 없음
            if(sum > n){
                break;
            }
        }
        

        if(n > sum){        // 최대값 범위를 줄여야 함
            min = mid +1;
        }else{              // 최소값 범위를 늘려야하는 경우
            max = mid -1;
//                if(sum == n){
            answer = Math.min(answer, mid);     // 28,29 둘다 답이 될수 있으므로, Math.min값 처리
//                }
        }
    }
    return answer;
}

전체 소스 코드(git)

[참조 블로그]

프로그래머스_입국심사
[JAVA] 프로그래머스 : 입국심사