AVL 트리란?
이진 탐색 트리의 한 종류
이진 트리와 이진 탐색 트리의 특징들을 모두 갖고 있다.
이진 트리의 특징
- 각 노드는 최대 2개의 자식 노드를 가질 수 있다.
- 자식 노드는 보통 왼쪽과 오른쪽으로 구분한다.
- 각 노드는 데이터를 가지고 있다.
이진 탐색 트리의 특징
- 이진트리이므로 이진트리의 특성을 기본적으로 갖고 있다.
- 각 노드의 값은 왼쪽 서브트리에 존재하는 모든 값보다 크고 오른쪽 서브트리에 존재하는 모든 값들 보다 작다.
- 정렬된 이진트리라고도 한다.
AVL 트리의 특징
- 어떤 노드라도 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1보다 크지 않다.
- 만약 특정 노드를 추가하거나 삭제했을 때 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1보다 커지는 노드가 생긴다면
re-balancing을 통해 1번 규칙에 어긋나지 않도록 한다. - 균형트리 이다.
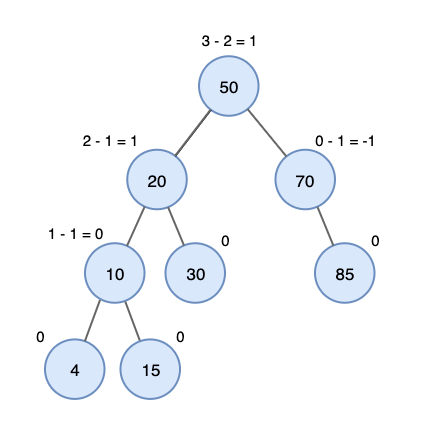
균형 인수 = 왼쪽 서브트리의 높이 - 오른쪽 서브트리의 높이
- 높이는 리프노드가
0이, NULL노드가-1이 되며 부모노드는 양쪽 자식 중큰 높이 + 1이 된다.
- 각 노드는 균형 인수를 가지고 있으며, 이 값은 항상 {-1, 0, 1} 중 하나여야 한다.
- 균형인수가 +이면 Left-heavy, 균형인수가 -면 Right-heavy이다.
회전
균형 인수가 -1, 0 , 1을 벗어난다면 회전으로 균형을 맞춘다.
각 상황마다 rotation에 방향을 달리함
case
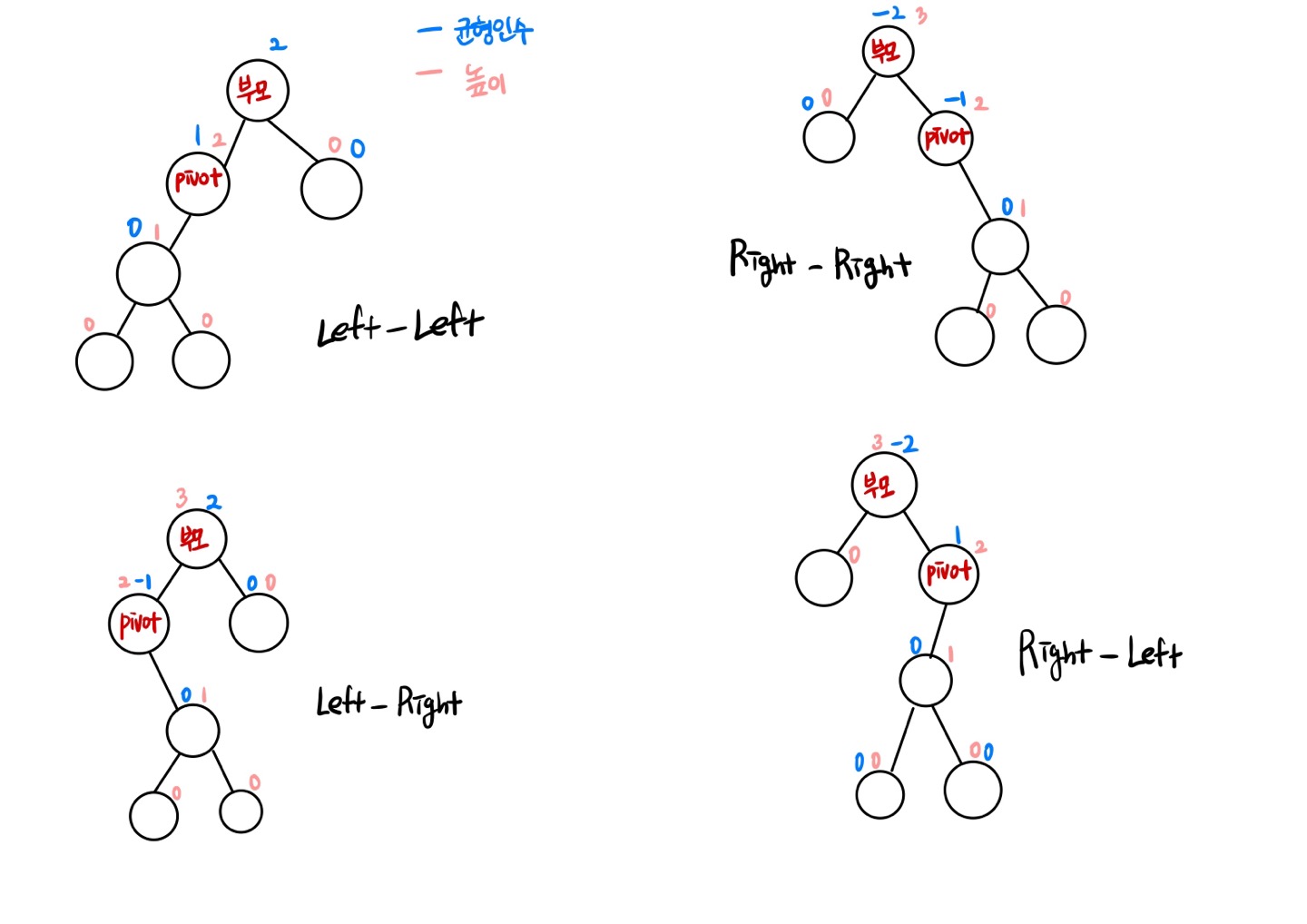
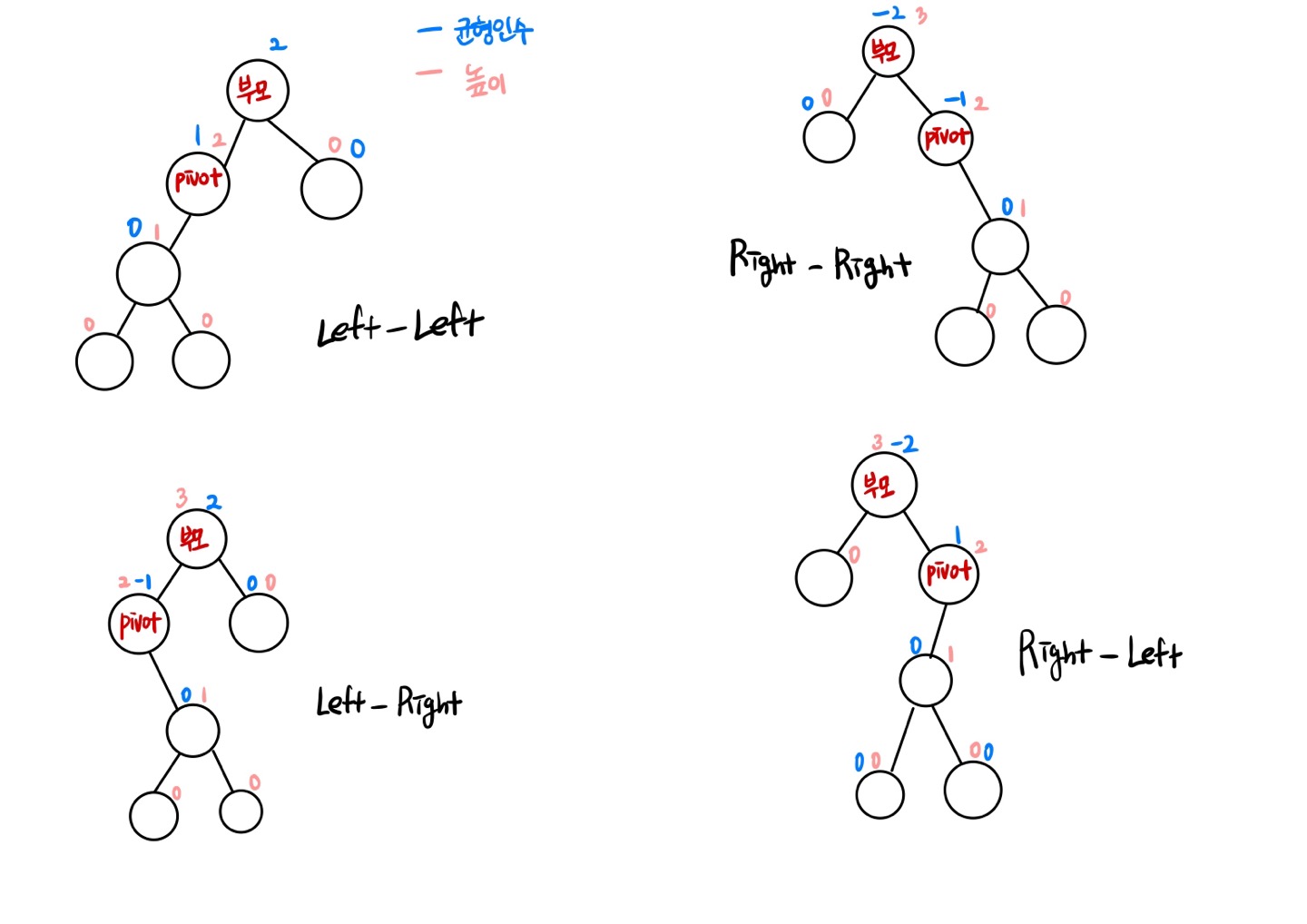
- LL(Left-Left) : 부모 노드와 pivot 노드의 균형인수가 모두 Left-heavy인 경우
- RR(Right-Right) : 부모 노드와 pivot 노드의 균형인수가 모두 Right-heavy인 경우
- LR(Left-Right) : 부모 노드 pivot 노드의 균형인수가 각각 Left-heavy, 우향인 경우
- RL(Right-Left) : 부모 노드와 pivot 노드의 균형인수가 각각 Right-heavy, Left-heavy인 경우
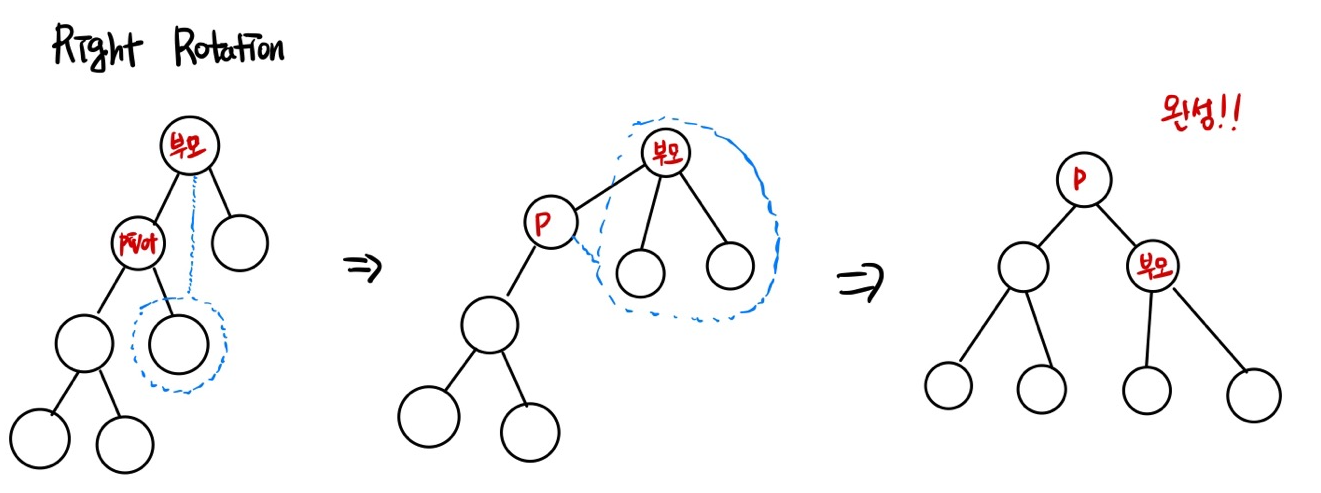
LL
right rotation 수행하여 균형을 맞춘다.
-
pivot 노드의 오른쪽 노드를 부모 노드의 왼쪽 노드로 만든다.
-
pivot 노드의 오른쪽 노드 자리에 부모 노드를 넣는다.
-
pivot 노드가 새로운 부모노드가 된다.
RR
left rotation 수행하여 균형을 맞춘다.
-
pivot 노드의 왼쪽 노드를 부모 노드의 오른쪽 노드로 만든다.
-
pivot 노드의 왼쪽 노드 자리에 부모 노드를 넣는다.
-
pivot 노드가 새로운 부모 노드가 된다.
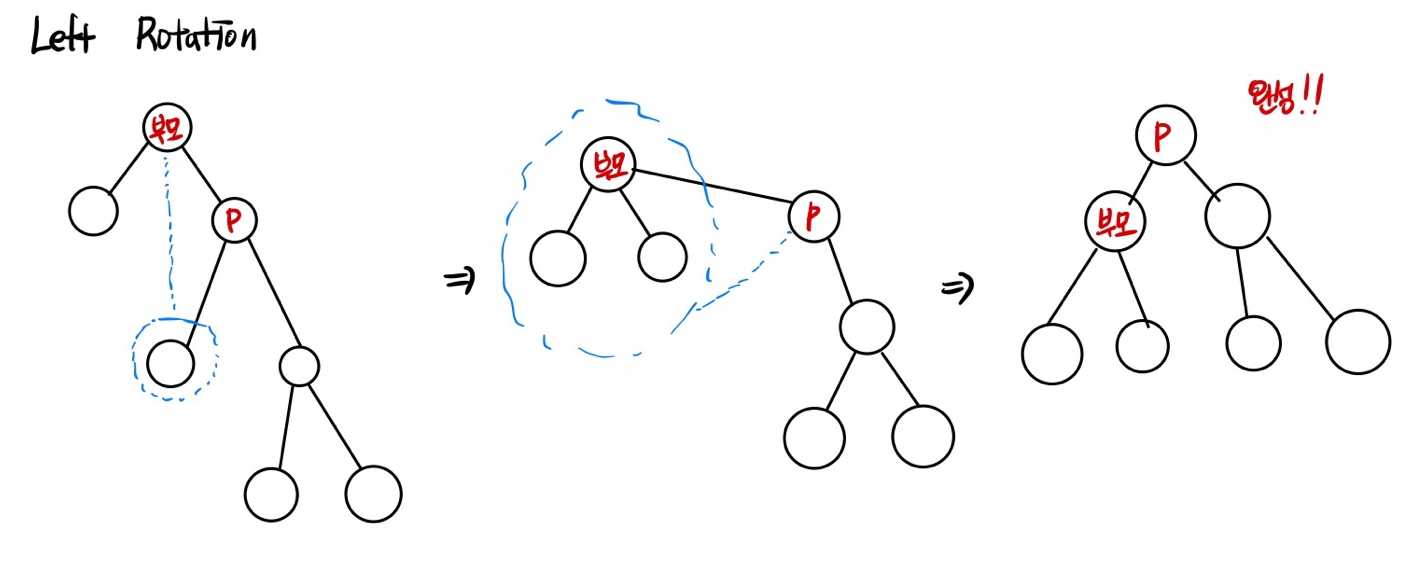
LR
- left rotation -> right rotation 총 두번의 rotation을 수행하여 균형을 맞춘다.
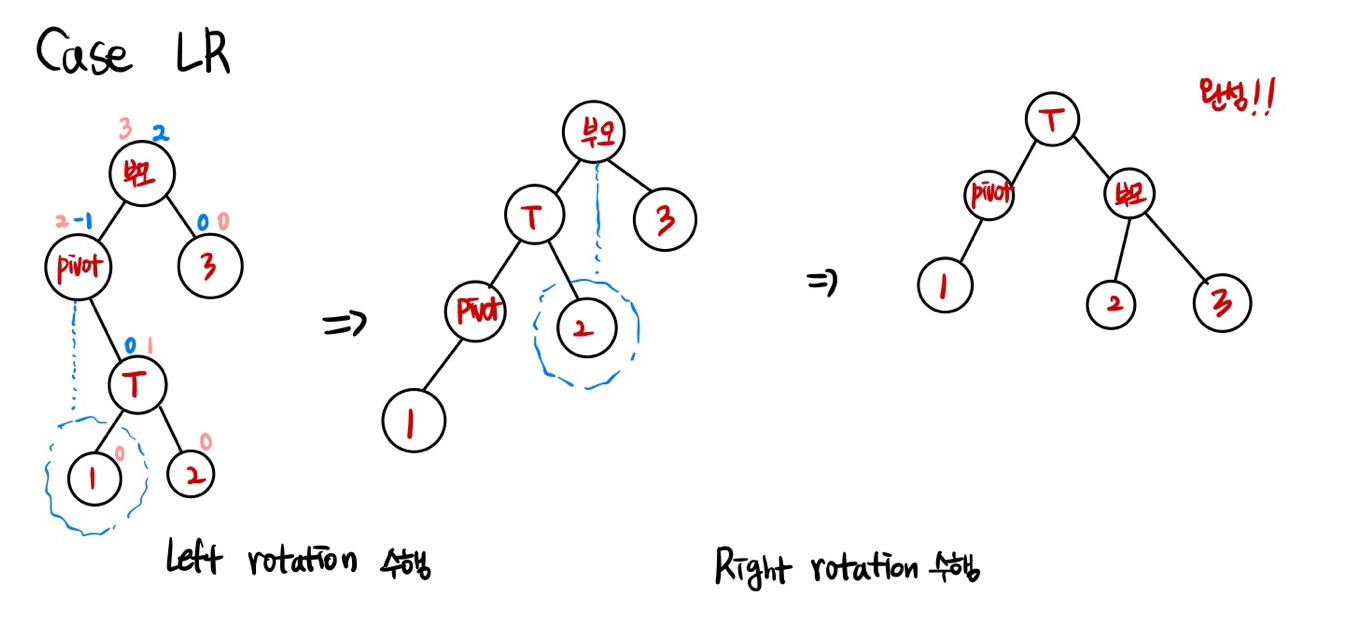
RL
- right rotation -> left rotation 총 두번의 rotation 을 수행하여 균형을 맞춘다.
장점
- 항상 트리의 검색이 O(logN)으로 균형잡혀 있다.
- 트리의 삽입과 삭제 또한 O(logN)
단점
- 구현이 어렵다.
- 빠르지만, 재균형 잡는 시간이 든다.
- 일반적으로 사용되는 균형 트리에 최적화된 다른 트리가 존재한다. (B-tree)
참고
https://chayan-memorias.tistory.com/157
https://yoongrammer.tistory.com/m/72
https://velog.io/@qqqqld/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-AVL-%ED%8A%B8%EB%A6%AC
https://keichee.tistory.com/441