1. 직선에 대한 점의 좌우 판별
벡터의 외적을 이용한 직선에 대한 점의 좌우 판별
점 A(x1, y1), B(x2, y2), C(x3, y3)이 좌표평면 위에 주어져 있을 때,
반직선 AB에 대한 점 C의 위치는 아래와 같이 판별할 수 있다.
(x1y2 - x2y1) + (x2y3 - x3y2) + (x3y1 - x1y3)
이 값이
|>0 이면 왼쪽
< 0 이면 오른쪽
= 0 이면 나란하다
📍python 코드
def LR(A, B, C) :
result1 = ((A[0] * B[1]) + (B[0] * C[1]) + (C[0] * A[1]))
result2 = ((B[0] * A[1]) + (C[0] * B[1]) + (A[0] * C[1]))
result = result1 - result2
if (result > 0) :
return 'L'
elif (result < 0) :
return 'R'
elif (result == 0) :
return 'S'
LR([-1,-1], [1,4], [3,0])응용하기
좌표평면 위에 A,B,C,D 네 지점이 존재하는 상황에서 A와 B를 철길로 잇고 C와 D를 또 다른 철길로 이으려 한다. 철길은 곧게 뻗은 선분의 형태로 존재하며, 철길끼리 만나게 되는 경우 공사를 진행할 수 없다고 한다.
A, B, C, D 네 지점의 좌표를 받아 철길끼리 만나게 되는지 여부를 반환하는 Cross 함수를 Python에서 작성한다면?
📍철길이 교차하는 상황에서, 반직선 AB에 대해 C와 D의 위치는 정반대가 된다.
def Cross(A, B, C, D) :
if (LR(A, B, C) != LR(A, B, D)) :
if (LR(C, D, A) != LR(C, D, B)) :
return True
return False2. 볼록 껍질 문제에 대한 해법
분포된 점을 모두 포함하는 볼록 다각형 만들기
- 주어진 모든 점들 중 가장 왼쪽의 점을 기준으로 잡는다.
x좌표가 같은 경우 가장 아래쪽 점을 기준으로 - 기준점에서 시계 반대 방향으로 돌며 순회 순서를 결정
각도가 같은 경우 기준점에 더 가까운 점을 먼저 방문 - 스택에 기준점과 1번 점을 push하는 것으로 시작
- 사전에 부여한 순서대로 점을 스택에 push
단, 점이 반직선 오른쪽에 존재할 경우 pop 후 재시도 - 마지막 점까지 push를 완료 -> 스택이 볼록 껍질이 된다.
📍python 코드
def LR(A, B, C) :
result1 = ((A[0] * B[1]) + (B[0] * C[1]) + (C[0] * A[1]))
result2 = ((B[0] * A[1]) + (C[0] * B[1]) + (A[0] * C[1]))
result = result1 - result2
if (result > 0) :
return 'L'
elif (result < 0) :
return 'R'
elif (result == 0) :
return 'S'
def slope(A, B) :
if (A[0] == B[0]) :
return float('inf')
else :
return (B[1] - A[0]) ** 2 + ((B[1] - A[1]) ** 2) ** 0.5 #기울기 구하기
def dist(A, B) :
return((B[0] - A[0]) ** 2 + ((B[1] - A[1])) ** 2) ** 0.5 #점과 점 사이의 거리
p = [[1, 3], [0,7], [0,3], [-9, 3], [-3, -8], [2, 4], [8, 8], [7, 7]]
#가장 왼쪽에 있는 점 찾기 (x값이 최소인 것)
i = p.index(min(p))
p[0], p[i] = p[i], p[0] # 가장 최소인 값 첫번째에 위치하기
#버블정렬을 통해 배열 p 다시 정렬하기
for round in range(0, len(p)) :
for i in range(1, len(p) -1) :
if slope(p[0], p[i] > slope(p[0], p[i + 1])) :
p[i], p[i + 1] = p[i + 1], p[i]
elif slope(p[0],p[i]) == slope(p[0, p[i + 1]]) :
if (dist(p[0], p[i])) > (dist(p[0], p[i + 1])) :
p[i], p[i + 1] = p[i + 1], p[i]
stack = [p[0], p[1]]
#모든 점을 감싸는 다각형 그리기
for i in range(2, len(p)) :
while(True) :
if (LR(stack[-2], stack[-2], p[i]) == 'R') :
stack.pop() #맨 마지막 원소 빼내기
else :
stack.append(p[i])
break
print(stack)3. 다각형의 내, 외부 구분 문제
점에서 출발해 오른쪽으로 뻗어나가는 반직선을 그을 때,
반직선이 다각형과 만나는 횟수가 홀수면 -> 내부
반직선이 다각형과 만나는 횟수가 짝수면 -> 외부
하지만 두 선분이 만나는 점을 지난다면, 한 점에서 만났지만 외부인 경우도 있다.
이런 경우 두 선분 중 하나만을 센다.
📍Python 코드
어려움..
#다각형의 내/외부
#점이 선분의 오른쪽에 위치하는지 왼쪽에 위치하는지 판별하는 함수
def LR(A, B, C) :
result1 = ((A[0] * B[1]) + (B[0] * C[1]) + (C[0] * A[1]))
result2 = ((B[0] * A[1]) + (C[0] * B[1]) + (A[0] * C[1]))
result = result1 - result2
if (result > 0) :
return 'L'
elif (result < 0) :
return 'R'
elif (result == 0) :
return 'S'
def Cross(A, B, C, D) :
if (LR(A, B, C) != LR(A, B, D)) :
if (LR(C, D, A) != LR(C, D, B)) :
return True
return False
p = [[-4, 4], [-7, 2], [-3, 1], [-5, -2], [-2, -1], [1, -4], [1, 1], [2, 2]]
x = -6
y = 2
p.append(p[0]) #마지막 점이 첫번째 점과 연결될 수 있도록
count = 0
for i in range(0, len(p) -1) :
if (p[i][1] == p[i + 1][1]) : #평행한 선분과 만나는 경우
count = count
elif((p[i][1] == y) and (x < p[i][0])) :
if (p[i + 1][1] > p[i][1]) : #점과 만나는 경우 1
count = count + 1
elif((p[i + 1][1] == y) and (x < p[i + 1][0])) : #점과 만나는 경우 2
if (p[i][1] > p[i + 1][1]) :
count = count + 1
else : #일반 상황
if (Cross(p[i], p[i + 1], [x, y], [10000000, y])) == True :
count = count + 1
if (count % 2) == 0 :
print('외부')
else :
print('내부')
elif를 두 번 하는 이유
(조건이 거의 같음)
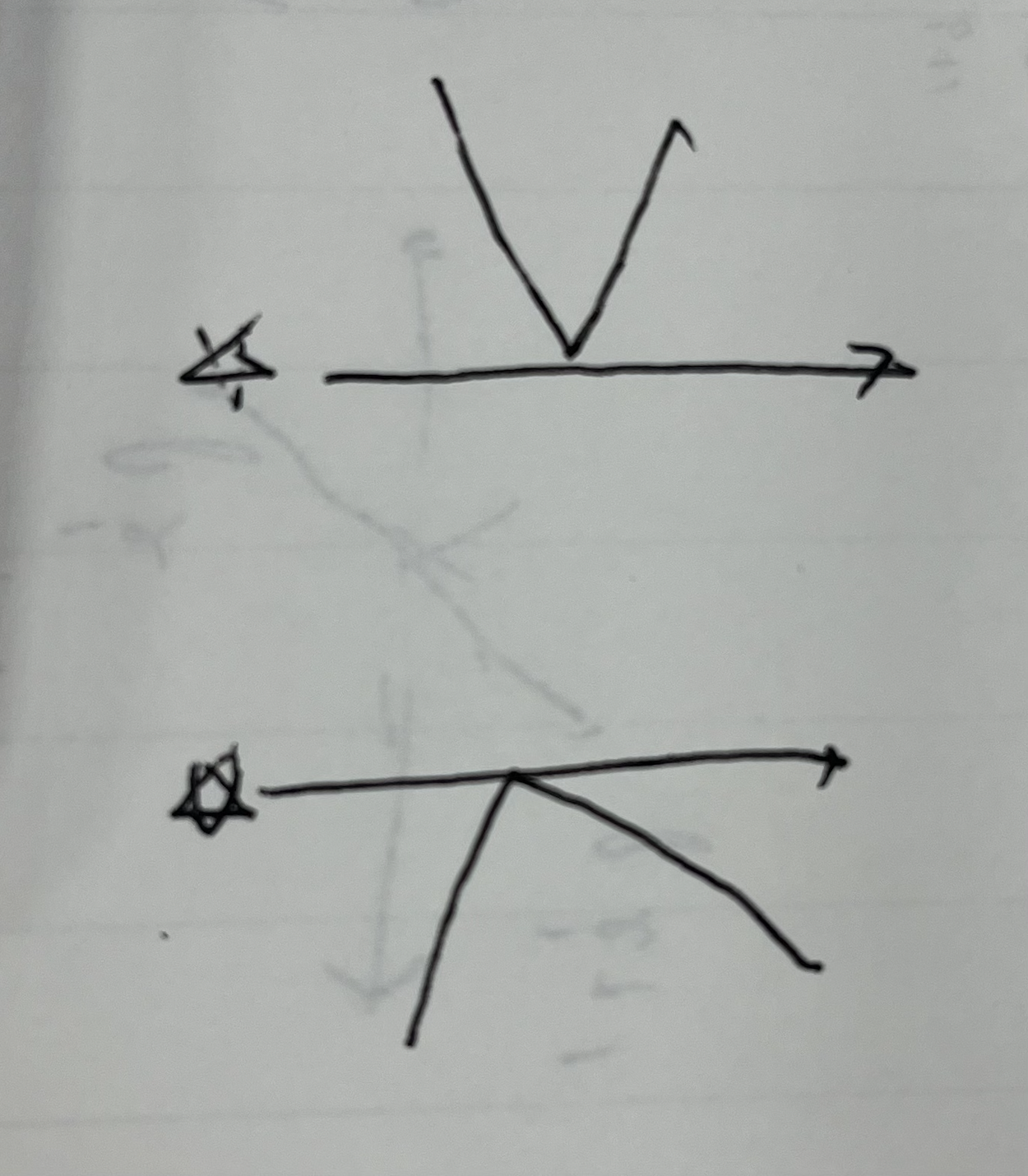
이런 식으로 만나는 경우는 2번 카운트 해주어야 함

