그래프
- 그래프는 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현
- 정점(Vertex) : 그래프의 구성요소로 하나의 연결점
- 간선(Edge) : 두 정점을 연결하는 선
- 차수(Degree) : 정점에 연결된 간선의 수
- 그래프는 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료 구조
- V: 정점의 개수, E : 그래프에 포함된 간선의 개수
- V개의 정점을 가지는 그래프는 최대 V*(V-1)/2 간선이 가능
예) 5개 정점이 있는 그래프의 최대 간선 수는 10(=>5*4/2)개이다.
- 선형 자료구조나 트리 자료구조로 표현하기 어려운 N : N 관계를 가지는 원소들을 표현할 때 용이
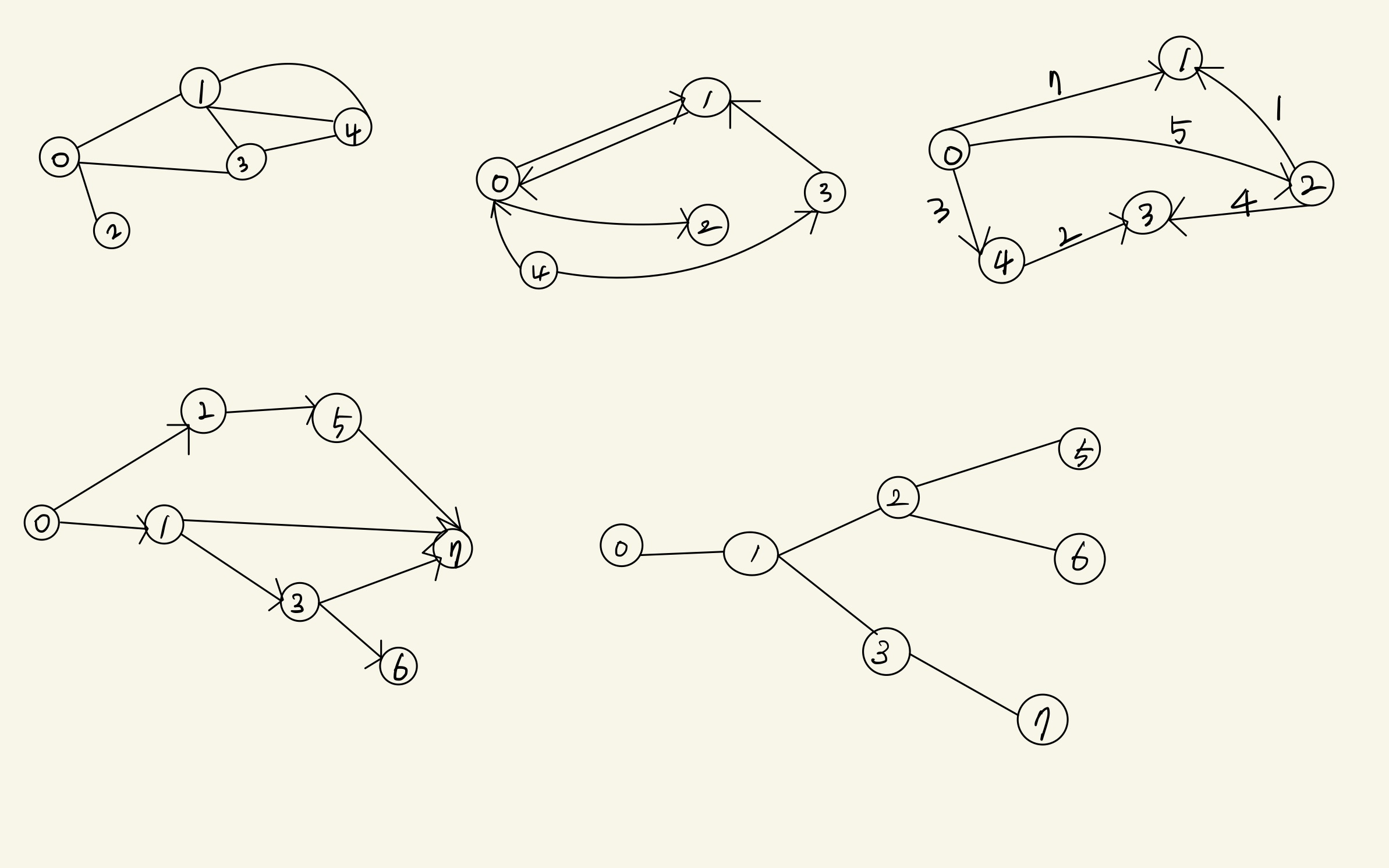
그래프 유형
-
무향 그래프
-
유향 그래프
-
가중치 그래프
-
사이클 없는 방향 그래프
-
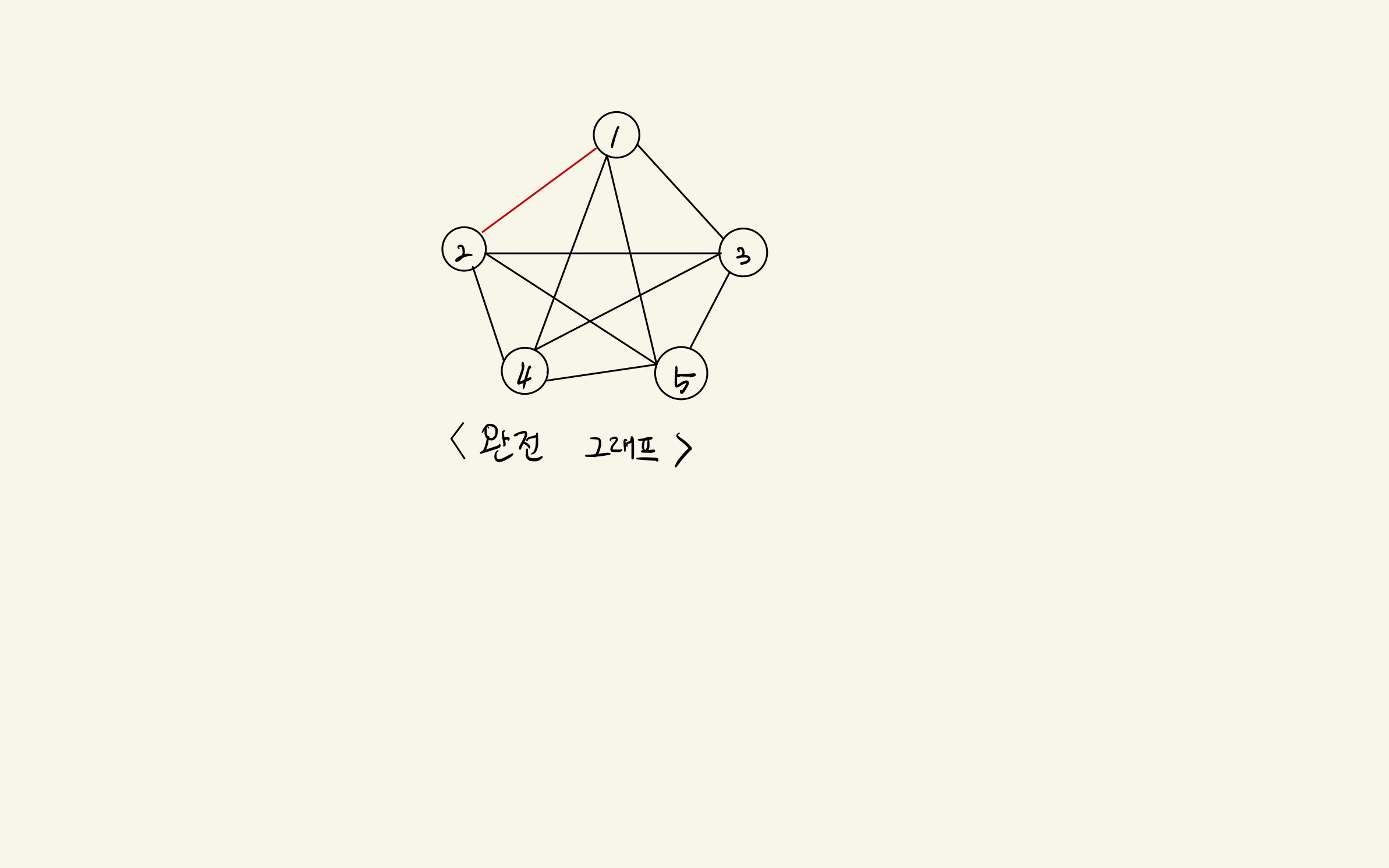
완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프
-
부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
-
트리도 그래프!!!
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재 가능
- 두 노드 사이에는 유일한 경로가 존재
인접 정점
-
인접(Adjacency)
- 두 개의 정점에 간선이 존재하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점들은 인접해 있다.
그래프 경로
- 경로는 어떤 정점 A에서 시작하여 다른 정점 B로 끝나는 순회로 두 정점 사이를 잇는 간선을들 순서대로 나열한 것
- 어떤 정점에서 다른 정점으로 가는 경로는 여러가지 일 수 있다.
- 단순 경로
- 시작 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 싸이클(Cycle)
- 경로의 시작 정점과 끝 정점이 같음
그래프 표현
-
간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
-
인접 행렬(Adjacent matrix)
- N x N 크기의 2차원 배열을 이용해서 간선 정보를 저장
- 배열의 배열
-
인접 리스트(Adjacent List)
- 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
-
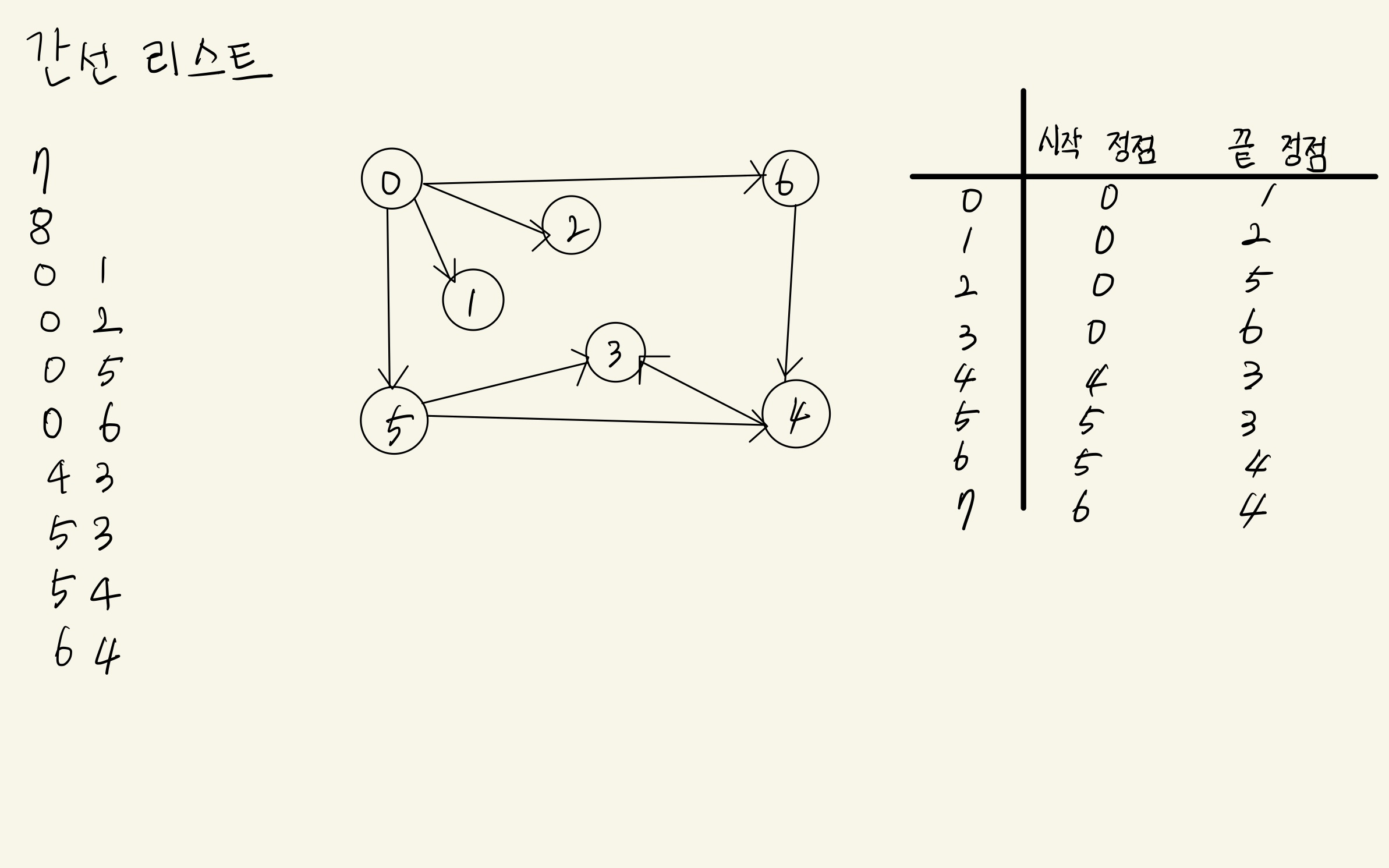
간선 리스트(Edge List)
- 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장
인접 행렬
- 두 정점을 연결하는 간선의 유무를 행렬로 표현
- N x N 정방 행렬
- 행 번호와 열 번호를 그래프의 정점에 대응
- 두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현
- 무향 그래프
- i번째 행의 합 = i번째 열의 합 = Vi의 차수
- i번째 행의 합 = i번째 열의 합 = Vi의 차수
- 유향 그래프
- 행 i의 합 = Vi의 진출 차수
- 열 i의 합 = Vi의 진입 차수
- 간선에 방향이 없는 무향 그래프의 경우에는, 노드 i -> 노드 j가 존재하면 노드 j -> 노드 i도 존재하는 것. 따라서 대각선을 기준으로 대칭인 성질을 가진다.
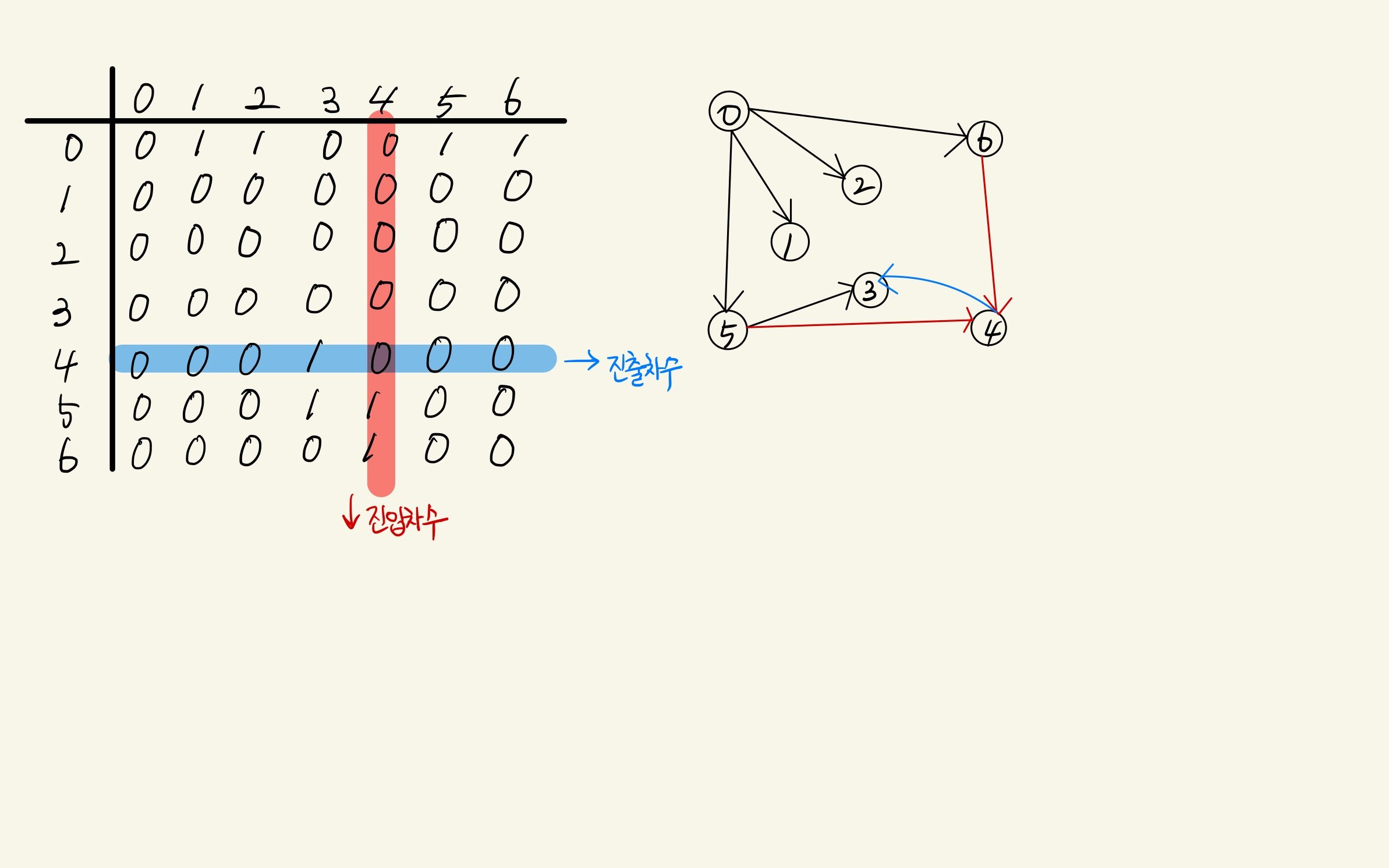
인접 행렬의 단점은??
- 메모리 낭비
- 노드의 개수가 간선의 개수보다 많다면 낭비이다.
인접 리스트
- 각 정점에 대한 인접 정점들을 순차적으로 표현
- 하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장

간선 리스트
- 두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트에 저장
- 간선을 표현하는 두 정점의 정보를 나타냄(시작 정점, 끝 정점)