백트래킹
- 모든 조합을 시도해서 문제의 해를 찾는다.
- 해를 얻을 때 까지 모든 가능성을 시도한다.
- 모든 가능성은 하나의 트리처럼 구성할 수 있으며, 가지 중에 해결책이 있다.
- 여러 선택지들 중 하나의 가지를 선택한다.
- 선택한 가지의 root 노드에서 leaf 노드 까지의 경로를 탐색하여 해답이 되는 가지를 지속적으로 선택
- 이 방법은 완전 탐색의 방법으로 해답이 될 가능성이 전혀 없는 노드의 다음(후손) 노드들도 모두 탐색해야 하므로 비효율적
따라서 백트래킹 기법이 등장
백트래킹은 한정 조건을 가진 문제를 풀려는 전략이다.
배제 와 풀이 시간의 단축이 백트래킹이 등장하게 된 배경이다.
어떤 노드의 유망성을 파악한 후, 유망하지 않으면 그 노드의 가지를 가지치기 해버린 후 다른 자손 노드를 검색하는 형식이다.
따라서 유망하지 않으면 가지치기(배제) 하고 부모노드로 되돌아가면서 풀이 시간이 단축되는 원리이다.
물론 대부분의 문제들에서 백트래킹보다는 DP나 그리디 알고리즘 방법으로 더 빠르게 해결할 수 있지만 백트래킹으로만 해결이 가능한 문제가 존재하기 때문에 그러한 조건일 때 백트래킹이 사용된다.
DFS와 백트래킹
- DFS
- DFS는 가능한 모든 경로를 탐색.
- 따라서 불필요할 것 같은 경로를 사전에 차단하는 방법이 없어 경우의 수를 줄일 수 없다.
- 백트래킹
- 이 경로가 유망하지 않다고(해가 될 것 같지 않다고) 판단하면 그 경로를 더 이상 가지 않고 부모노드로 되돌아간다.
- 경우의 수를 줄일 수 있으므로 효율적이다.
- 즉, 백트래킹은 모든 가능한 경우의 수 중 특정 조건을 만족하는 경우만 지속적으로 살펴보는 것
백트래킹 활용(N-Queen)
크기가 N x N 인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 구해라.
4 x 4 인 체스판 일 때
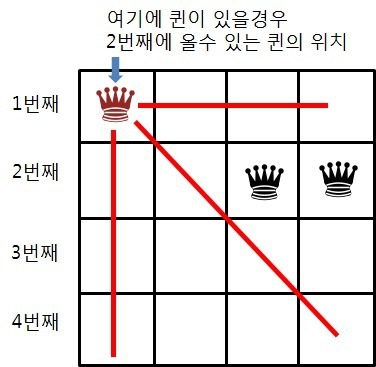
빨간색 선이 퀸이 이동할 수 있는 경로이고, 첫 번째 퀸과 두 번째 퀸이 서로 공격할 수 없게 배치하기 위해서는 3,4 번째 칸에 두 번째 퀸을 놓아야 한다.
즉, 우리는 2번째 행에 퀸을 3,4 번째 칸에 놓은 경우만 탐색하면 된다.
(2번째 행에 1,2 번째 칸에 퀸을 놓았다면 유망하지 않기 때문에 가지치기)
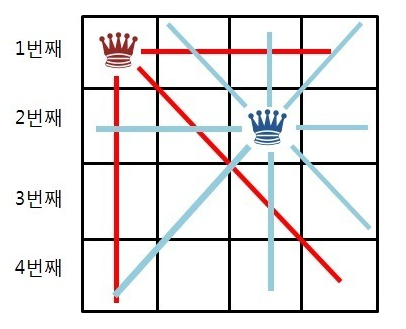
2번째 행의 3열에 퀸을 놓았을 경우 3번째 행에 놓을 수 있는 열은 없기 때문에 가지치기 된다.
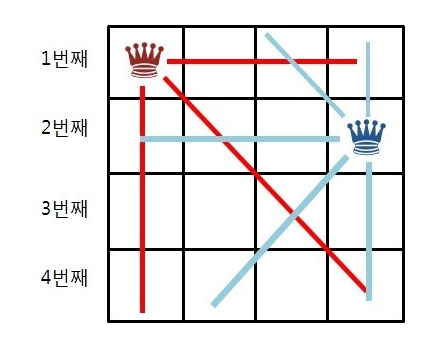
2번째 행의 4열에 퀸을 놓았을 경우 3번째 행에 놓을 수 있는 곳은 2열밖에 없다.
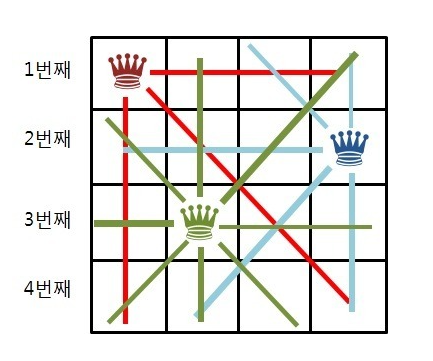
3번째 행의 2열에 퀸을 놓은 경우, 4번째 행에 둘 수 있는 공간은 없기 때문에 최종적으로
1행의 1열에 퀸을 놓았을 경우 유망한 가지는 하나도 없다는 결론이 나온다.
똑같은 방법으로 첫번째 행의 2열,3열,4열에 퀸을 놓았을 때를 계산해보면 2가지방법이 존재한다.
첫 번째 경우
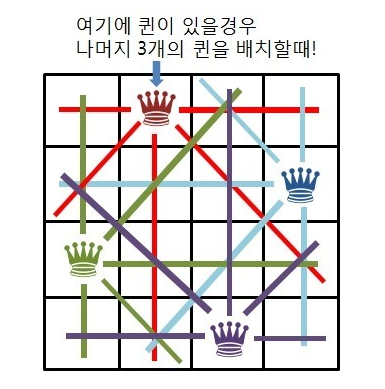
두 번째 경우
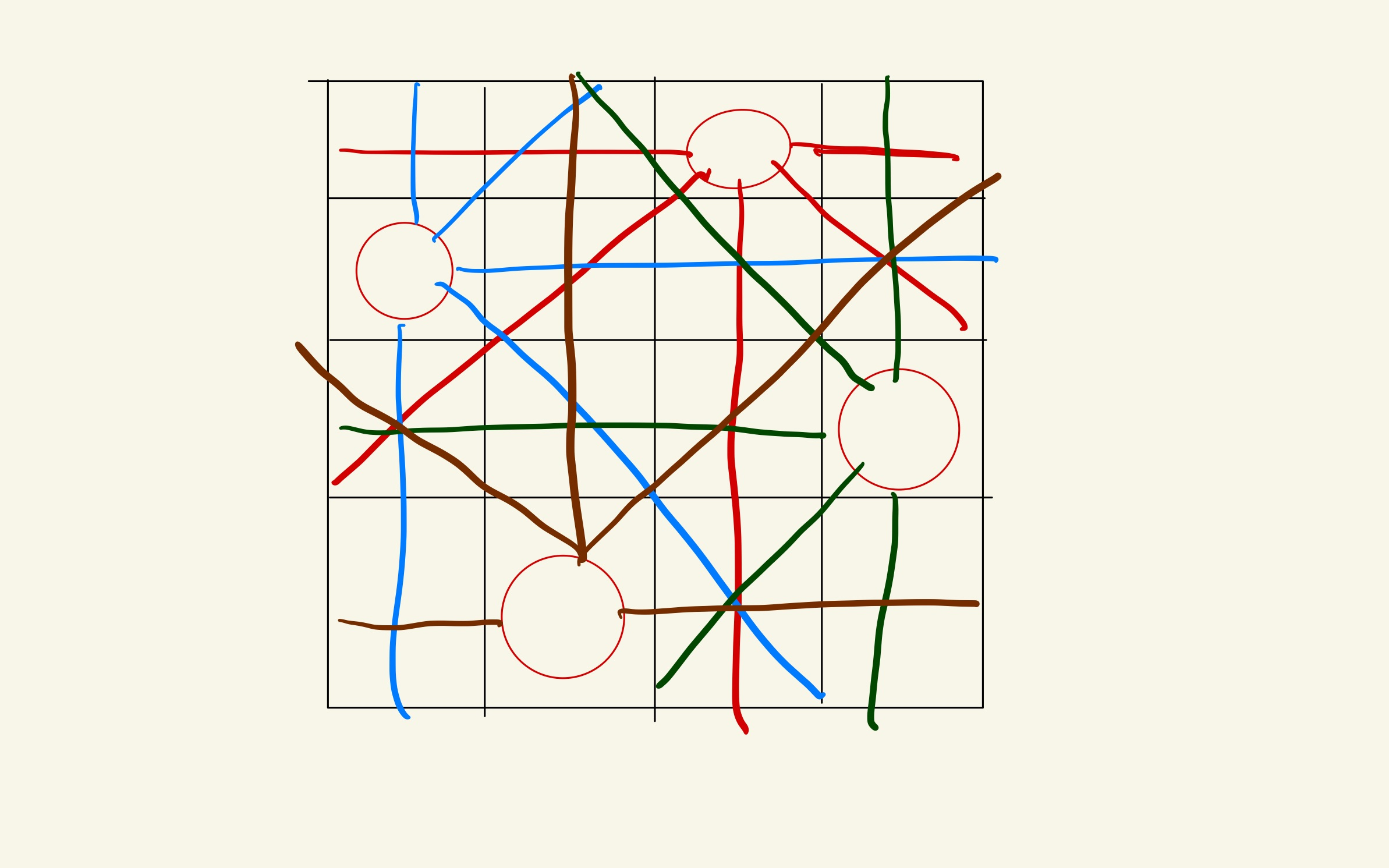
백트래킹 활용(특정 조건을 만족하는 부분집합)
결론
백트래킹은 해답을 찾는 과정에서 해답이 될 가능성이 있는지를 확인하고 가능성이 없다고 판단하면 더이상 깊게 들어가지 않고 부모 노드로 돌아가는 방식을 보여준다.
백트래킹을 사용하지 않고 DFS를 사용했을 경우 첫번째 해답을 찾았을 때 검색해야하는 노드의 개수는 155번째로 시도하다가 첫 번째 해답인 (2열-4열-1열-3열)을 발견하지만
백트래킹을 사용했을 경우에는 27번째의 시도만에 해답을 찾을 수 있다.
