트리 탐색 - BFS, DFS

BFS(Breadth First Search)

• 너비 우선 탐색
• BFS는 루트 노드의 자식 노드들을 먼저 모두 차례로 방문한 후에, 방문했던 자식 노드들을 기준으로 하여 다시 해당 노드의 자식 노드들을 차례로 방문하는 방식
• 인접한 노드들에 대해 탐색을 한 후, 차례로 다시 BFS를 진행해야 하므로, FIFO 형태의 자료구조 큐를 활용

BFS 알고리즘

BFS start

• 큐 생성
• 루트를 큐에 삽입
• while(!queue.isempty)
• p <- 큐의 첫 번째 원소 빼내기
• p 방문
• for(p와 연결된 모든 간선)
• c <- t의 자식 노드
• c를 큐에 삽입
  End BFS

DFS(Depth First Search)

• 깊이 우선 탐색
• 루트 노드에서 출발하여 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 노드로 되돌아와 다른 방향의 노드로 탐색을 계속 반복하여 결국 모든 노드를 방문하는 순회 알고리즘
• 가장 마지막에 만났던 갈림길의 노드로 되돌아가 다시 DFS를 반복해야 하므로 재귀로 구현하거나 LIFO 구조의 스택 사용

DFS 알고리즘

DFS(루트)
루트 방문
for(루트의 모든 자식 노드 c)
DFS(c)
end DFS

이진트리의 순회

• 순회 : 트리의 노드들을 체계적으로 방문하는 것
• 3가지의 기본적인 순회방법
  • 전위순회(루트->왼쪽 자식노드->오른쪽 자식노드)
  • 중위순회(왼쪽 자식노드->루트->오른쪽 자식노드)
  • 후위순회(왼쪽 자식노드->오른쪽 자식노드->루트)

전위 순회(preorder traversal)

• 수행 방법
  • 현재 노드 T를 방문해서 처리 - 부모노드
  • 현재 노드 T의 왼쪽 자식노드로 이동 - 왼쪽 자식 노드
  • 현재 노드 T의 오른쪽 자식 노드로 이동 - 오른쪽 자식 노드
• 알고리즘

preorder_traverse(T){
	if(T is not null) {
    	visit(T);
        preorder_traverse(T.left);
        preorder_traverse(T.right);
    }
}

중위 순회(inorder traversal)

• 수행 방법

  • 현재 노드 T의 왼쪽 자식노드로 이동 - 왼쪽 자식 노드
  • 현재 노드 T를 방문해서 처리 - 부모 노드
  • 현재 노드 T의 오른쪽 자식노드로 이동 - 오른쪽 자식 노드

• 알고리즘

inorder_traverse(T){
	if(T is not null){
    	inorder_traverse(T.left);
        visit(T);
        inorder_traverse(T.right);
    }
}

후위 순회(postorder traversal)

• 수행 방법

  • 현재 노드 T의 왼쪽 자식노드로 이동 - 왼쪽 자식 노드
  • 현재 노드 T의 오른쪽 자식노드로 이동 - 오른쪽 자식 노드
  • 현재 노드 T를 방문해서 처리 - 부모 노드

• 알고리즘

postorder_traverse(T){
	if(T is not null){
    	postorder_traverse(T.left);
        postorder_traverse(T.right);
        visit(T);
    }
}

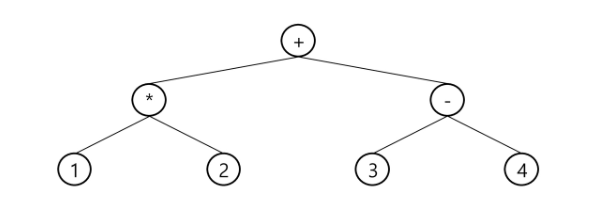
수식트리

• 수식을 표현하는 이진 트리
• 수식 이진 트리(Expression Binary Tree)라고 부르기도 한다.
• 연산자는 루트 노드이거나 가지 노드
• 피연산자(숫자)는 모두 leaf노드