Chapter 01. 자료구조와 알고리즘의 이해

김민정·2024년 10월 10일

윤성우 열혈 자료구조

목록 보기

1/14

`<Intro>`

오랜만에 돌아온 기술 블로그~🖐🏻
인턴십 마무리와 댄스팀 촬영, 적절한 휴식기를 가지고 다시 공부 시작~
오늘 SSAFY 13기 모집 공고💻가 떴다!
내년에 SSAFY에서 교육을 듣는다면 내후년에 취업은 문제 없지 않을까...?!

c언어-python-Java 가보자구~~✨

우선 오늘은 C언어를 사용하여 자료구조를 배워보자~!

01-1 "자료구조(Data Structure)에 대한 기본적인 이해"

C언어의 문법과 관련해서 알고 있어야 하는 부분

우선 C언어를 사용해서 자료구조를 배우기 위해서는 아래와 같은 부분은 알고 있다고 가정하고 진행하려한다.

나와 같이 C언어를 학습했다면 위에 부분은 어느정도 기초 지식을 가지고 이해가 보다 쉬울 수 있다.
어려운 분들이 계신다면 열혈 C언어📚에서 문법을 확인하면서 같이 알아가는 것도 좋을 것 같다.

자료구조란?

자료구조란? 프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다.
위에서 말한 데이터를 표현은 데이터 저장을 포함하는 개념이고 데이터의 저장을 담당하는 것이 바로 자료구조이다.
넓은 의미에서 int형 변수도, 구조체의 정의도 자료구조에 속한다. (배열 또한 동일하다.)

이러한 자료구조는 기본적으로 다음과 같이 분류할 수 있다.

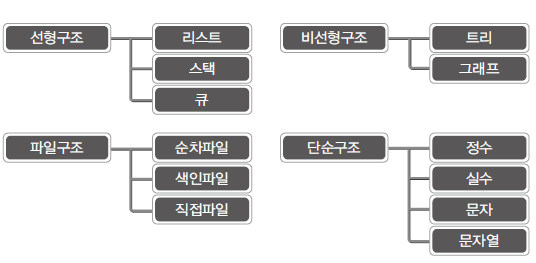
이 중에서 선형구조와 비선형구조에 대해 배울 것이다.
선형 자료구조는 데이터를 선의 형태로 나란히 혹은 일렬로 저장하는 방식이다.
비선형 자료구조는 데이터를 나란히 저장하지 않는 구조다.
따라서 선형 자료구조에 비해 비선형 자료구조는 상대적으로 어렵다.

알고리즘이란?

자료구조가 데이터의 표현 및 저장방법을 뜻한다면, 알고리즘은 표현 및 저장된 데이터를 대상으로 하는 문제의 해결 방법을 뜻한다.
따라서 자료구조가 결정되어야 그에 따른 효율적인 알고리즘을 결정할 수 있고,
자료구조에 따라 알고리즘이 달라진다.

01-2 "알고리즘의 성능분석 방법"

알고리즘의 성능분석을 위해서는 지수식( $y=2^x$ )과 로그식( $=log_2x$ )을 알고 있어야한다.

*시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)

좋은 성능의 자료구조와 알고리즘을 분석하고 평가하기 위해서 시간 복잡도와 공간 복잡도를 활용한다.
시간 복잡도(Time Complexity)는 속도에 해당하는 알고리즘의 수행시간 분석결과를 가리키며,
공간 복잡도(Space Complexity)는 메모리 사용량에 대한 분석결과를 가리킨다.
일반적으로 알고리즘을 평가할 때는 메모리의 사용량보다 실행속도에 초점을 둔다.
(메모리는 이전에 그 크기가 작았기 때문에 메모리의 사용량에 대한 중요도가 높았다면 메모리 용량이 큰 요즘에는 그 중요도가 조금 낮아졌다 볼 수 있다.)

그렇다면 알고리즘의 수행속도를 어떻게 알 수 있을까?
우선 연산의 횟수를 세고, 처리해야할 데이터의 수 $n$ 에 대한 연산횟수의 $T(n)$ 을 구성한다.
이렇듯 연산 횟수에 대한 식을 구성하면 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단할 수 있다. 또한, 둘 이상의 알고리즘을 비교하기 용이하다.

순차 탐색 알고리즘(Linear Search Algorithm)과 시간 복잡도 분석의 핵심요소

순차 탐색 알고리즘(Linear Search Algorithm)에 대한 간단한 탐색 알고리즘을 예제로 살펴보자.

#include <stdio.h>

int LSearch(int ar[], int len, int target)	// 순차 탐색 알고리즘 적용된 함수
{
	int i;
	for (i = 0; i < len; i++)
		if (ar[i] == target)
			return i;	// 찾은 대상의 인덱스 값 반환
	return -1;	// 찾지 못했음을 의미하는 값 반환
}

int main()
{
	int arr[] = { 3, 5, 2, 4, 9 };
	int idx;

	idx = LSearch(arr, sizeof(arr) / sizeof(int), 4);
	if (idx == -1)
		printf("탐색 실패 \n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	idx = LSearch(arr, sizeof(arr) / sizeof(int), 7);
	if (idx == -1)
		printf("탐색 실패 \n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);
	
	return 0;
}

> 출력
타겟 저장 인덱스: 3 
탐색 실패

위 예제는 맨 앞에서부터 순서대로 탐색을 진행하는 알고리즘이기때문에 순차 탐색이라는 이름이 붙었다.
순차 탐색 알고리즘을 실제로 구현하는 코드만 별도로 본다면 아래와 같다.

for (i = 0; i < len; i++)
	if (ar[i] == target)
		return i;	// 찾은 대상의 인덱스 값 반환
return -1;	// 찾지 못했음을 의미하는 값 반환

위 코드를 토대로 시간 복잡도를 분석해서 데이터의 수 n에 대한 연산횟수의 함수 $T(n)$ 을 구하기 위해서는 값의 동등을 비교하는 ==연산 횟수를 대상으로 분석하면 된다.
더불어 동등 비교 연산을 적게 수행하는 탐색 알고리즘이 좋은 탐색 알고리즘이다.

모든 알고리즘에는 가장 행복한 경우(운이 좋은 경우)와 가장 우울한 경우(운이 없는 경우)가 있는데 이를 최선의 경우(best case) 그리고 최악의 경우(worst case)라 한다.
알고리즘의 시간 복잡도를 분석할 때는 최악의 경우를 생각하는 것이 중요하다.
최선의 경우와 최악의 경우의 평균을 구하는 것도 좋은 방법일 수 있지만,
어떤 것이 평균적인 상황인지는 다양한 자료들이 수집되어야 하기 때문에 최악의 경우를 시간 복잡도로 선택하게 된다.

순차 탐색 알고리즘 시간 복잡도 계산 1: 최악의 경우(worst case)

위에서 소개한 예제를 기준으로 최악의 경우를 살펴보자면 찾으려는 값이 배열에서 마지막에 있을 경우로 "데이터 수가 $n$ 개 일때 최악의 경우에 해당하는 연산횟수(비교연산 횟수는) $n$ 이다."

따라서 시간 복잡도는 $T(n) = n$ 이 된다.

순차 탐색 알고리즘 시간 복잡도 계산 2: 평균적인 경우(average case)

평균적인 경우를 대상으로 $T(n)$ 함수를 정의해볼 것이다.
평균적인 경우의 연산횟수 계산을 위해 다음 두 가지 가정을 할 것이다.

가정 1. 탐색 대상이 배열에 존재하지 않을 확률을 50%라고 가정한다.
가정 2. 배열의 첫 요소부터 마지막 요소까지, 탐색 대상이 존재할 확률은 동일하다.

그럼 배열에 탐색 대상이 존재하는 경우와 존재하지 않는 경우를 나눠서 연산횟수를 계산할 것이고 우선 배열에 탐색 대상이 존재하지 않는 경우를 생각해보자.
데이터의 수가 n개일 때, 총 n번의 비교연산을 진행한다.
따라서 탐색 대상이 존재하지 않는 경우의 연산 횟수는 $n$ 이다.

이번에는 탐색 대상이 존재하는 경우의 연산횟수를 계산해 보자.
이 경우에는 $n \over 2$ 가 된다.

탐색 대상이 존재하지 않을 확률과 존재할 경우 확률이 각각 50%이기 때문에
순차 탐색 알고리즘의 평균적인 경우의 시간 복잡도 함수는 다음과 같다.
$T(n) = n×{1 \over 2}+{n \over 2}×{1 \over 2} = {3 \over 4}n$

최악의 경우에 비해 평균적인 경우 시간 복잡도 계산이 더 오래 걸리고 신뢰도가 높지 않다. 앞서 정의한 두 개의 가정을 뒷받침할 근거가 부족하기 때문이다.
따라서, 시간 복잡도는 '최악의 경우'를 기준으로 계산된다.

*이진 탐색 알고리즘(Binary Search Algorithm)

이진 탐색 알고리즘은 순차 탐색보다 훨씬 좋은 성능을 보인다. 단, 정렬된 데이터가 아니면 적용이 어렵다는 조건이 있다.

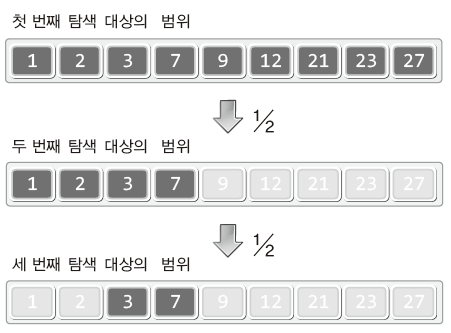
이진 탐색 알고리즘의 원리를 알기 위해서 우선 길이가 9인 배열을 다음과 같이 정렬된 상태로 데이터가 저장되어 있다 생각하자.
배열 이름은 arr이고, 이 배열을 대상으로 숫자 3이 저장되어 있는지 확인하기 위해서 이진 탐색 알고리즘을 사용할 것이다.

이진 탐색 알고리즘의 첫 번째 시도는 다음과 같다.

👉이진 탐색 알고리즘의 첫 번째 시도:
1. 배열 인덱스의 시작과 끝은 각각 0과 8이다.
2. 0과 8을 합하여 그 결과를 2로 나눈다.
3. 2로 나눠서 얻은 결과 4를 인덱스 값으로 하여 arr[4]에 저장된 값이 3인지 확인한다.

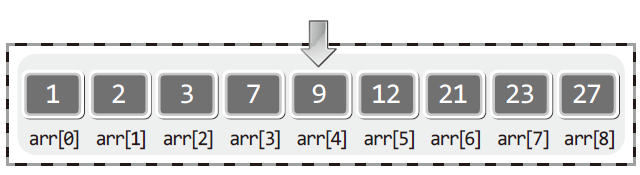
첫 번째 시도를 통해 arr[4]에 3이 저장되지 않았음을 확인했다.
두 번째 시도를 진행한다.

👉이진 탐색 알고리즘의 두 번째 시도:
1. arr[4]에 저장된 값 9와 탐색 대상 3의 대소를 비교한다.
2. 대소의 비교결과는 arr[4]>3이므로 탐색의 범위를 인덱스 기준 0~3으로 제한한다.
3. 0과 3을 더하여 그 결과를 2로 나눈다. 이때 나머지는 버린다.
4. 2로 나눠서 얻은 결과가 1이니 arr[2]에 저장된 값이 3인지 확인한다.

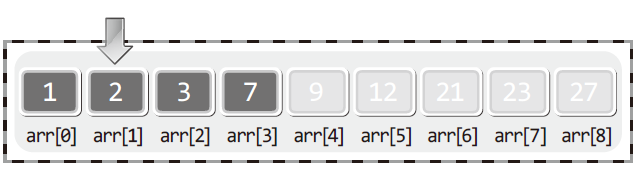
이진 탐색 알고리즘의 핵심이 여기서 나온다. 탐색의 대상을 절반으로 줄였다는 것이다.

arr[1]에도 3이 저장되어 있지 않았으니 두 번째 시도와 비슷하게 세 번째 시도를 진행한다.

👉이진 탐색 알고리즘의 세 번째 시도:
1. arr[1]에 저장된 값 2와 탐색 대상인 3의 대소를 비교한다.
2. 대소의 비교결과는 arr[1]<3이므로 탐색의 범위를 인덱스 기준 2~3으로 제한한다.
3. 2와 3을 더하여 그 결과를 2로 나눈다. 이때 나머지는 버린다.
4. 2로 나눠서 얻은 결과가 2이니 arr[2]에 저장된 값이 3인지 확인한다.

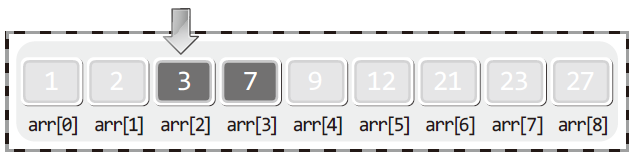
세 번째 시도에서 탐색 대상인 3을 찾게 되어 탐색은 마무리 되었다.

이렇듯 이진 탐색 알고리즘은 탐색의 대상을 반복해서 반씩 제외하는 방법의 알고리즘이다.

이진 탐색 알고리즘의 구현

이제 이진 탐색 알고리즘을 구현해보려고 한다.
구현하기 전에 탐색의 범위가 줄어드는 형태를 그림을 통해 다시 한번 상기시켜 보자.

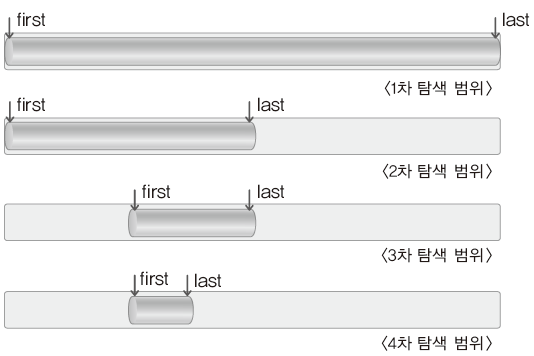
탐색의 시작위치에 해당하는 인덱스 값을 first, 탐색의 마지막 위치에 해당하는 인덱스 값을 last로 표시하고 있다.
그림과 같이 이진 탐색 알고리즘이 진행됨에 따라 first와 last는 가까워진다. 이진 탐색 알고리즘은 first와 last가 만날 때까지 진행되며 first가 last보다 커지게 되면 탐색의 대상이 존재하지 않음을 뜻하기 때문에 탐색을 종료하게 된다.
따라서 구현하는 부분에서 while문의 조건이 first <= last인 것을 명심하자.

#include <stdio.h>

int BSearch(int ar[], int len, int target)
{
	int first = 0;	// 탐색 대상의 시작 인덱스 값
	int last = len - 1;	// 탐색 대상의 마지막 인덱스 값
	int mid;

	while (first <= last)
	{
		mid = (first + last) / 2;	// 탐색 대상의 중앙을 찾기
		if (target == ar[mid])	//  중앙에 저장된 것이 타겟이라면
			return mid;	// 탐색 완료.
		else  // 타겟 탐색 안됐다면 탐색 대상 범위 반으로 줄이기
		{
			if (target <= ar[mid])
				last = mid - 1;	// 중간값 보다 작을 경우 탐색 대상 마지막 인덱스를 중간값보다 하나 작게하여 범위 축소
			else
				first = mid + 1;	// 중간값 보다 클 경우 탐색 대상 시작 인덱스를 중간값보다 하나 많게하여 범위 축소
		}
	}
	return -1;	// 찾지 못했을 때 -1 반환
}

int main()
{
	int arr[] = { 1, 3, 5, 7, 9 };
	int idx;

	idx = BSearch(arr, sizeof(arr) / sizeof(int), 7);
	if (idx == -1)
		printf("탐색 실패 \n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	idx = BSearch(arr, sizeof(arr) / sizeof(int), 4);
	if (idx == -1)
		printf("탐색 실패 \n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	return 0;
}

> 출력
타겟 저장 인덱스: 3 
탐색 실패

여기서 last = mid - 1이고 first = mid + 1인 이유는 mid에 저장된 인덱스 값의 배열요소도 새로운 탐색의 범위에 포함이 되어야하기 때문이다.
단순히 last = mid이고 first = mid로 코드를 작성한다면 기본적으로 세 변수에 저장된 인덱스 값이 first ≤ mid ≤ last이기 때문에 first에 저장된 값이 last보다 커질 수 없게 된다.

이진 탐색 알고리즘의 시간 복잡도 계산하기: 최악의 경우 기준

이진 탐색 알고리즘의 일부를 보면서 연산횟수를 대표하는 연산이 무엇인지 찾아보자.

while (first <= last)
{
	mid = (first + last) / 2;
	if (target == ar[mid])
		return mid;
	else
	{
		if (target <= ar[mid])
			last = mid - 1;
		else
			first = mid + 1;
	}
}

데이터의 수가 n개 일 때 최악의 경우 비교 연산이 총 몇번 이루어질까?

$n$ 이 1이 되기까지 2로 나눈 횟수 $k$ 회, 비교연산 $k$ 회 진행.
데이터가 1개 남았을 때 마지막으로 비교연산 1회 진행

👉 $T(n) = k + 1$

$k$ 는 어떻게 구할까?

$n × ({1\over2})^k = 1$ 이기 때문에 $k = log_2n$ 이 된다.

따라서 최악의 경우에 대한 시간 복잡도 함수 $T(n)$ 은 $log_2n$ 이 된다.
정확하게 얘기하면 $T(n) = log_2n + 1$ 이 아닌가?라고 할 수 있다.
시간 복잡도 자체가 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단하는 것이기 때문에 1은 전체 연산횟수에 대해 미치는 영향이 미미해 생략이 가능하다.

이 상수항의 생략과 관련된 것이 빅-오 표기법이다.

빅-오 표기법(Big-Oh Notation)

빅-오 표기법이란 함수 $T(n)$ 에서 가장 영향력이 큰 부분을 표기하는 방법이다.
만약 시간 복잡도 함수가 $T(n) = n^2 + 2n +1$ 이라면
이를 빅-오 표기법으로 나타냈을 때 $O(n^2)$ 가 된다.

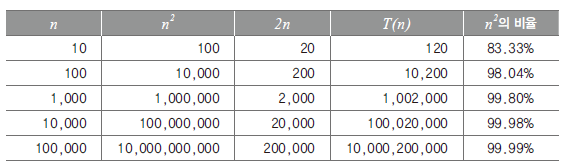
n의 크기가 증가함에 따라 시간 복잡도 함수에서 가장 영향력이 있는 항은 최고차항이게 된다.
정리하자면, 시간 복잡도 함수 $T(n) = n^2 + 2n +1$ 의 빅오는 $O(n^2)$ 이며 $n$ 의 증가 및 감소에 따른 $T(n)$ 의 변화 정도가 $n^2$ 의 형태를 띈다.

대표적인 빅-오

데이터 수의 증가에 따른 연산횟수의 증가 형태를 표현한 것이 빅-오이다 보니 대표적인 빅-오 표기는 다음과 같다.

$O(1)$
: 상수형 빅-오로 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘이다.
$O(logn)$
: 로그형 빅-오로 데이터 수의 증가율에 비해서 연산횟수의 증가율이 훨씬 낮은 알고리즘을 의미한다.
$O(n)$
: 선형 빅-오로 데이터의 수와 연산횟수가 비례하는 알고리즘을 의미한다.
$O(nlogn)$
: 선형로그형 빅-오로 데이터의 수가 두배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘을 의미한다.
$O(n^2)$
: 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다. 중첩된 반복문의 사용으로 알고리즘 디자인에서 그리 바람직한 것은 아니다.
$O(n^3)$
: 데이터 수의 세 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다. 삼중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우 발생한다.
$O(2^n)$
: 지수형 빅-오로 사용한다는 것 자체가 비현실적인 알고리즘이다.

지금까지 소개된 빅-오 표기들의 성능(수행시간, 연산횟수)의 대소를 정리하면 다음과 같다.

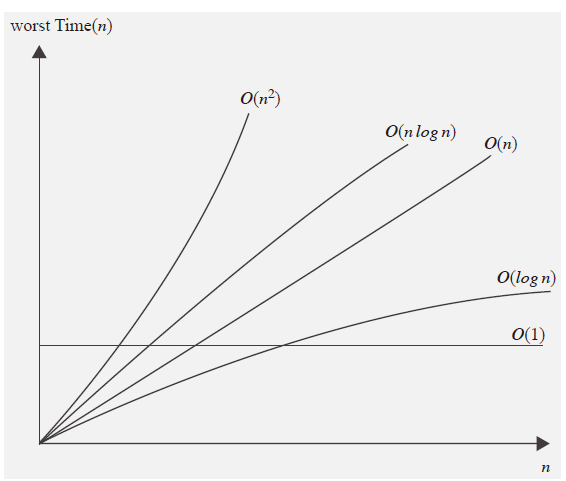
순차 탐색 알고리즘과 이진 탐색 알고리즘 비교

두 탐색 알고리즘의 빅-오를 판단해 비교해보자.
두 탐색 알고리즘의 시간 복잡도 함수 $T(n)$ (최악의 경우)를 우선 살펴보자.

$T(n) = n$ : 순차 탐색 알고리즘 $T(n)$ 함수
$T(n) = log_2n+1$ : 이진 탐색 알고리즘 $T(n)$ 함수

따라서 빅-오 표기는 다음과 같다.

$O(n)$ : 순차 탐색 알고리즘 빅-오
$O(logn)$ : 이진 탐색 알고리즘 빅-오

이 두 빅-오 간의 성능 차이를 보기 위해 두 알고리즘의 비교연산횟수를 수치적으로 비교해볼 것이다.

최악의 경우를 대상으로 비교하는 것이 목적이니 탐색의 실패를 유도한다.
탐색의 실패가 결정되기까지 몇 번의 비교연산이 진행되는지 센다.
데이터의 수는 500, 5000, 50000일 때를 기준으로 각각 실험을 진행한다.

$O(n)$ 의 경우 데이터 수와 동일하게 비교연산 횟수가 진행되므로,
$O(logn)$ 의 경우를 예재를 통해서 살펴보자.

#include <stdio.h>

int BSearch(int ar[], int len, int target)
{
	int first = 0;
	int last = len - 1;
	int mid;
	int opCount = 0;	// 비교연산의 횟수를 기록

	while (first <= last)
	{
		mid = (first + last) / 2;
		if (target == ar[mid])
			return mid;
		else
		{
			if (target < ar[mid])
				last = mid - 1;
			else
				first = mid + 1;
		}
		opCount += 1;	// 비교연산의 횟수 1 증가
	}
	printf("비교연산횟수: %d \n", opCount);
	return -1;
}

int main()
{
	int arr1[500] = { 0, };
	int arr2[5000] = { 0, };
	int arr3[50000] = { 0, };	// 모든 요소 0으로 초기화
	int idx;

	// 배열 arr1을 대상으로, 저장되지 않은 정수 1을 찾으라고 명령
	idx = BSearch(arr1, sizeof(arr1) / sizeof(int), 1);
	if (idx == -1)
		printf("탐색 실패 \n\n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	// 배열 arr2을 대상으로, 저장되지 않은 정수 2을 찾으라고 명령
	idx = BSearch(arr2, sizeof(arr2) / sizeof(int), 2);
	if (idx == -1)
		printf("탐색 실패 \n\n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	// 배열 arr3을 대상으로, 저장되지 않은 정수 3을 찾으라고 명령
	idx = BSearch(arr3, sizeof(arr3) / sizeof(int), 3);
	if (idx == -1)
		printf("탐색 실패 \n\n");
	else
		printf("타겟 저장 인덱스: %d \n", idx);

	return 0;
}

> 출력
비교연산횟수: 9  
탐색 실패        

비교연산횟수: 13 
탐색 실패        

비교연산횟수: 16 
탐색 실패